Die Bürgerinitiative veranstaltet am viel besuchten Badesee der Gemeinde eine Unterschriftenaktion gegen die geplante Windkraftanlage.
Berechnen Sie, wie hoch der Anteil \(p\) der Gegner der Windkraftanlage unter den Badegästen mindestens sein muss, damit sich unter zehn zufällig ausgewählten Badegästen mit einer Wahrscheinlichkeit von mindestens 99 % wenigstens ein Gegner der Windkraftanlage befindet.
(5 BE)
Lösung zu Teilaufgabe 3
Binomialverteilung
Binomialverteilte Zufallsgröße
Für eine Zufallsgröße \(X\), welche bei einer Bernoulli-Kette der Länge \(n\) die Anzahl der Treffer \(k \in \{0,1,\dots,n\}\) mit der Trefferwahrscheinlichkeit \(p\) angibt, gilt:
Binomialverteilung (vgl. Merkhilfe)
\[P_{p}^{n}(X = k) = B(n;p;k) = \binom{n}{k} \cdot p^{k} \cdot (1 - p)^{n - k} \quad (0 \leq k \leq n)\]
Eine Binomialverteilung ist durch die Parameter \(n\) und \(p\) eindeutig bestimmt und wird durch das Symbol \(B(n:p)\) gekennzeichnet. \(X\) heißt binomialverteilt nach \(B(n;p)\).
Voraussetzung für eine Binomialverteilung
Ein Zufallsexperiment, bei dem nur zwei sich gegenseitig ausschließende Ereignisse \(A\) und \(\overline{A}\) mit konstanten Wahrscheinlichkeiten eintreten können (Bernoulli-Experiment).
Zufallsgröße \(G \colon \enspace\) "Anzahl der Gegner der Windkraftanlage unter den Badegästen"
Analyse der Angabe:
"... unter zehn zufällig ausgewählten Badegästen ..."
\[\Longrightarrow \quad n = 10\]
"... wenigstens ein Gegner der Windkraftanlage ..."
\[\Longrightarrow \quad G \geq 1\]
"... mit einer Wahrscheinlichkeit von mindestens 99 % ..."
\[\Longrightarrow \quad P^{10}_p(G \geq 1) \geq 0{,}99\]
Betrachten des Gegenereignisses
Betrachten des Gegenereignisses (mindestens 1 Treffer)
Wahrscheinlichkeitsberechnungen einer binomialverteilten Zufallsgröße \(X\) der Form „mindestens 1 Treffer" \(P(X \geq 1)\) vereinfachen sich durch die Betrachtung des Gegenereignisses „nicht 0 Treffer":
\[P(X \geq 1) = 1 - P(X = 0)\]
Formel von Bernoulli
Wahrscheinlichkeit für genau \(k\) Treffer bei einer Bernoullikette der Länge \(n\) und der Trefferwahrscheinlichkeit \(p\) für das Eintreten eines betrachteten Ereignisses:
\[P(X = k) = B(n;p;k) = \binom{n}{k} \cdot p^k \cdot (1 - p)^{n - k}\]
\[k \in \{0,1,\dots,n\}\]
\[\begin {align*}P_p^{10}(G \geq 1) &\geq 0{,}99 & &| \; \text{Gegenereignis formulieren} \\[0.8em] 1 - P_p^{10}(G = 0) &\geq 0{,}99 & &| -1 \\[0.8em] -P_p^{10}(G = 0) &\geq -0{,}01 & &| \cdot (-1) \quad \text{Relationszeichen dreht!} \\[0.8em] P_p^{10} (G = 0) &\leq 0{,}01 & &| \; \text{Formel von Bernoulli anwenden} \\[0.8em] \underbrace{\binom{10}{0}}_{1} \cdot \underbrace{p^{0}}_{1} \cdot (1 - p)^{10 - 0} &\leq 0{}01 & &| \; \sqrt[10]{\quad} \\[0.8em] 1 - p &\leq \sqrt[10]{0{,}01} & &| -1 \\[0.8em] -p &\leq \sqrt[10]{0{,}01} - 1 & &| \cdot (-1) \quad \text{Relationszeichen dreht!} \\[0.8em] p &\geq 1 - \sqrt[10]{0{,}01} \end {align*}\]
\[1 - \sqrt[10]{0{,}01}\approx 0{,}37 = 37 \; \%\]
Der Anteil \(p\) der Gegner der Windkraftanlage unter den Badegästen muss mindestens 37 % betragen.
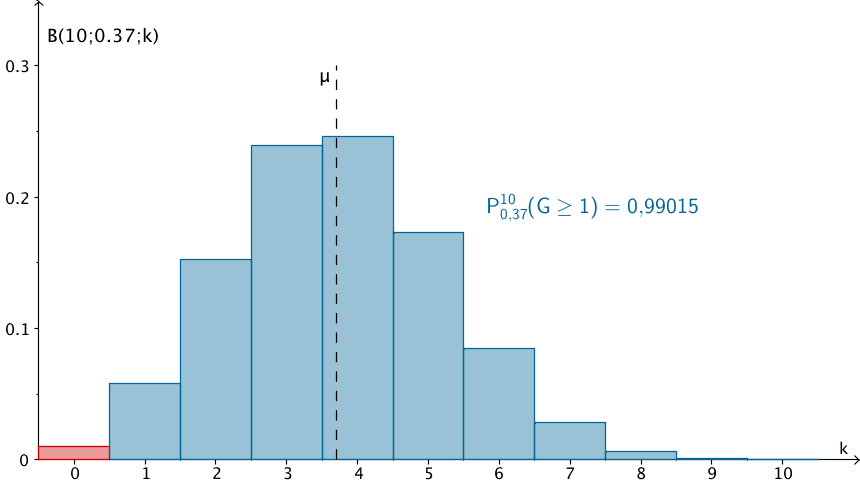
Kumulative Wahrscheinlichkeit \(\,P^{10}_{0{,}37}(G \geq 1)\,\) der nach \(\,B(10;0{,}37)\,\) binomialverteilten Zufallsgröße \(\,G\,\)
