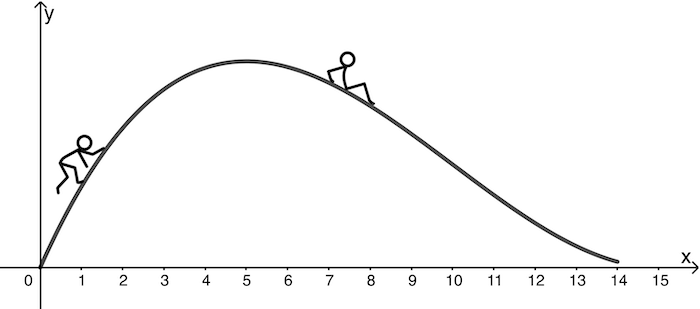
Die Abbildung zeigt modellhaft den Verlauf einer Wasserrutsche, der näherungsweise durch die Funktion \(f \colon x \mapsto 0{,}01x^3 -0{,}3x^2 + 2{,}25x\) mit \(D_f = [0:14]\) beschrieben wird. Eine Längeneinheit im Koordinatensystem entspricht 0,5 m in der Realität.
a) Bestimmen Sie die maximale Höhe der Rutsche durch Rechnung.
b) Berechnen Sie das mittlere Gefälle der Rutsche im Intervall \([6;10]\).
c) Beschreiben Sie die wesentlichen Schritte, um die steilste Stelle der Rutsche im Intervall \([5;14]\) rechnerisch zu ermitteln.
a) Bestimmung der maximalen Höhe der Rutsche
\[f(x) = 0{,}01x^3 -0{,}3x^2 + 2{,}25x; \; D_f = [0;14]\]
Notwendige Bedingung für eine Extremstelle von \(f\):
Extremstelle(n) bestimmen mit Vorzeichenwechsel der 1. Ableitung
Ist eine Funktion \(f\) in einem Intervall \(I =\, ]a;b[\) differenzierbar und \(x_0\) eine innere Stelle von \(I\), so gilt:
Wenn \(\textcolor{#cc071e}{f'(x_0) = 0}\) ist und \(\textcolor{#cc071e}{f'}\) bei \(x_0\) einen Vorzeichenwechsel
von \(\textcolor{#cc071e}{+}\) nach \(\textcolor{#cc071e}{–}\) hat, dann besitzt \(f\) an der Stelle \(x_0\) ein lokales Maximum \(f(x_0)\).
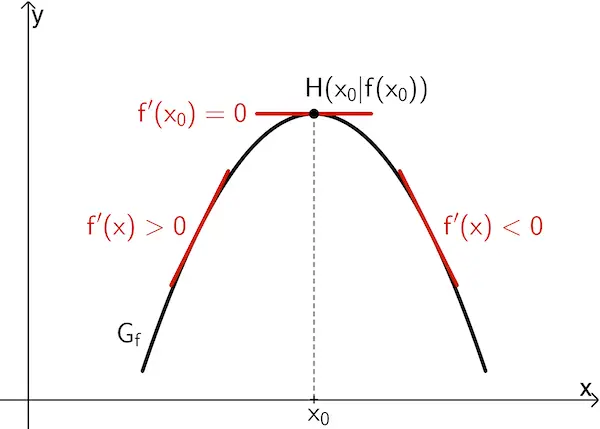
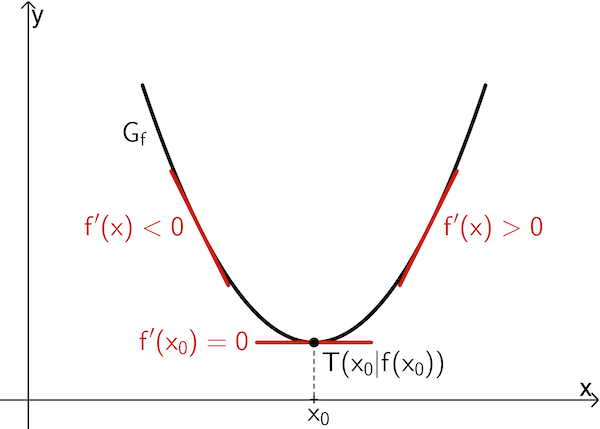
von \(\textcolor{#cc071e}{–}\) nach \(\textcolor{#cc071e}{+}\) hat, dann besitzt \(f\) an der Stelle \(x_0\) ein lokales Minimum \(f(x_0)\).
\[f'(x) = 0\]
Erste Ableitung \(\boldsymbol{f'}\) bilden
Benötigte Ableitungen/Ableitungsregel: Faktorregel, Summenregel, Potenzregel (Ableitung einer Potenzfunktion)
\[f(x) = 0{,}01x^3 -0{,}3x^2 + 2{,}25x\]

Ableitungen der Grundfunktionen
\[c' = 0 \enspace (c \in \mathbb R)\]
\[\left( x^r \right)' = r \cdot x^{r - 1} \enspace (r \in \mathbb R)\]
\[\left( \sqrt{x} \right)' = \frac{1}{2\sqrt{x}}\]
\[\left( \sin{x} \right)' = \cos{x}\]
\[\left( \cos{x} \right)' = -\sin{x}\]
\[\left( \ln{x} \right)' = \frac{1}{x}\]
\[\left( \log_{a}{x}\right)' = \frac{1}{x \cdot \ln{a}}\]
\[\left( e^x \right)' = e^x\]
\[\left(a^x \right)' = a^x \cdot \ln{a}\]
vgl. Merkhilfe
Faktorregel
\[\begin{align*}f(x) &= a \cdot \textcolor{#0087c1}{u(x)} \\[0.8em] f'(x) &= a \cdot \textcolor{#0087c1}{u'(x)}\end{align*}\]
Summenregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(x)} + \textcolor{#cc071e}{v(x)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(x)} + \textcolor{#cc071e}{v'(x)}\end{align*}\]
Produktregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v(x)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(x)} \cdot \textcolor{#cc071e}{v(x)} + \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v'(x)}\end{align*}\]
Quotientenregel
\[\begin{align*}f(x) &= \dfrac{\textcolor{#0087c1}{u(x)}}{\textcolor{#cc071e}{v(x)}} \\[0.8em] f'(x) &= \dfrac{\textcolor{#0087c1}{u'(x)} \cdot \textcolor{#cc071e}{v(x)} - \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v'(x)}}{[\textcolor{#cc071e}{v(x)}]^{2}}\end{align*}\]
Kettenregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(}\textcolor{#cc071e}{v(x)}\textcolor{#0087c1}{)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(}\textcolor{#cc071e}{v(x)}\textcolor{#0087c1}{)} \cdot \textcolor{#cc071e}{v'(x)}\end{align*}\]
vgl. Merkhilfe
\[\begin{align*}f'(x) &= 0{,}01 \cdot 3x^2 - 0{,}3 \cdot 2x + 2{,}25 \\[0.8em] &= 0{,}03x^2 - 0{,}6x + 2{,}25\end{align*}\]
Nullstelle(n) von \(\boldsymbol{f'}\) bestimmen
\[\begin{align*} f'(x) &= 0 \\[0.8em]0{,}03x^2 - 0{,}6x + 2{,}25 &= 0 &&| \; \text{„Mitternachtsformel" anwenden} \end{align*}\]
Lösungsformel für quadratische Gleichungen (vgl. Merkhilfe)
\[ax^2 + bx + c = 0 \,, \qquad a, b, c \in \mathbb R \,, \quad a \neq 0\]
\[\begin{align*} x_{1,2} &= \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}, \quad b^2 \geq 4ac \\[0.8em] x_{1,2} &= \frac{-b \pm \sqrt{D}}{2a}, \quad D \geq 0 \end{align*}\]
Diskriminante \(D = b^2 -4ac \;\):
\(D < 0\,\): keine Lösung
\(D = 0\,\): genau eine Lösung
\(D > 0\,\): zwei verschiedene Lösungen
\[\begin{align*} x_{1,2} &= \frac{0{,}6 \pm \sqrt{(-0{,}6)^2 - 4 \cdot 0{,}03 \cdot 2{,}25}}{2 \cdot 0{,}03} \\[0.8em] &= \frac{0{,}6 \pm \sqrt{0{,}09}}{0{,}06} = \frac{0{,}6 \pm 0{,}3}{0{,}06} = 10 \pm 5\end{align*}\]
\[\Rightarrow \; x_1 = 5;\; (x_2 = 15 \textcolor{#cc071e}{\notin} D_f)\]
Die Abbildung bestätigt, dass der Graph der Funktion \(f\) bei \(\textcolor{#e9b509}{x = 5}\) ein Maximum hat. Ein weiterer Nachweis ist nicht nötig.
Maximale Höhe der Rutsche berechnen
„Eine Längeneinheit im Koordinatensystem entspricht 0,5 m in der Realität." (vgl. Angabe)
\[f(\textcolor{#e9b509}{5}) = 0{,}01 \cdot \textcolor{#e9b509}{5}^3 - 0{,}3 \cdot \textcolor{#e9b509}{5}^2 + 2{,}25 \cdot \textcolor{#e9b509}{5} = 5\]
\[5 \cdot 0{,}5\,\text{m} = 2{,}5\,\text{m}\]
Die maximale Höhe der Rutsche beträgt 2,5 m.
Ergänzung: Nachweis des Maximums (nicht verlangt)
Mit einer Monotonietabelle
| \(x\) | \([0;5[\) | \(5\) | \(]5;14]\) |
| \(f'(x)\) | \(\textcolor{#0087c1}{\boldsymbol{+}}\) | \(0\) | \(\textcolor{#cc071e}{\boldsymbol{–}}\) |
| \(G_f\) | \(\textcolor{#0087c1}{\boldsymbol{\nearrow}}\) | \(\text{Max.}\) | \(\textcolor{#cc071e}{\boldsymbol{\searrow}}\) |
Testwerte z.B.: \(f'(4) = 0{,}33 \textcolor{#0087c1}{> 0}; \; f'(6) = -0{,}27 \textcolor{#cc071e}{< 0}\)
Mit der zweiten Ableitung
Extremstelle(n) bestimmen mit Vorzeichen der 2. Ableitung
Ist eine Funktion \(f\) in einem Intervall \(I =\, ]a;b[\) zweimal differenzierbar und \(x_0\) eine innere Stelle von \(I\), so gilt:
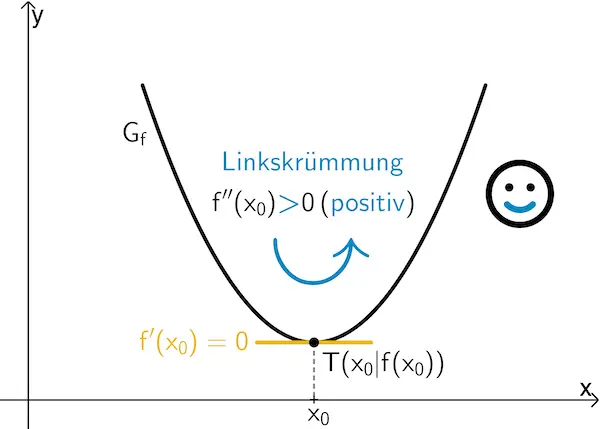
Wenn \(\textcolor{#e9b509}{f'(x_0) = 0}\) und \(f''(x_0) \textcolor{#cc071e}{\boldsymbol{<}} 0\) ist, dann besitzt \(f\) an der Stelle \(x_0\) ein lokales Maximum \(f(x_0)\).
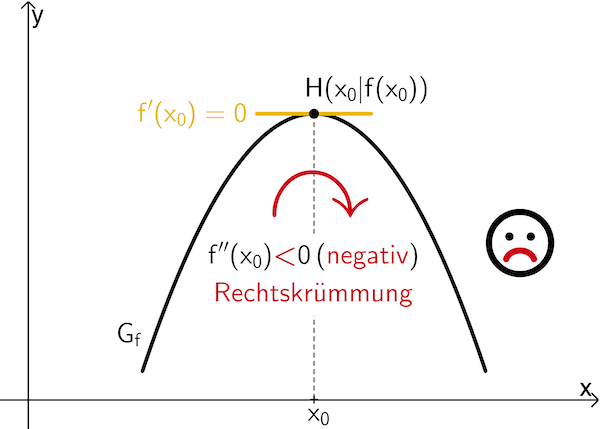
Wenn \(\textcolor{#e9b509}{f'(x_0) = 0}\) und \(f''(x_0) \textcolor{#0087c1}{\boldsymbol{>}} 0\) ist, dann besitzt \(f\) an der Stelle \(x_0\) ein lokales Minimum \(f(x_0)\).
\[f'(x) = 0{,}03x^2 - 0{,}6x + 2{,}25\]
\[f''(x) = 0{,}06x - 0{,}6\]
\(f''(\textcolor{#e9b509}{5}) = 0{,}06 \cdot \textcolor{#e9b509}{5} - 0{,}6 = -0{,}3 \textcolor{#cc071e}{< 0} \Rightarrow\) lokales Maximum
(Merkhilfe: ![]() negativ, Rechtskrümmung \(\Rightarrow\) lokales Maximum)
negativ, Rechtskrümmung \(\Rightarrow\) lokales Maximum)
b) Berechnung des mittleren Gefälles der Rutsche im Intervall \([6;10]\)
 (Skizze nicht verlangt)
(Skizze nicht verlangt)
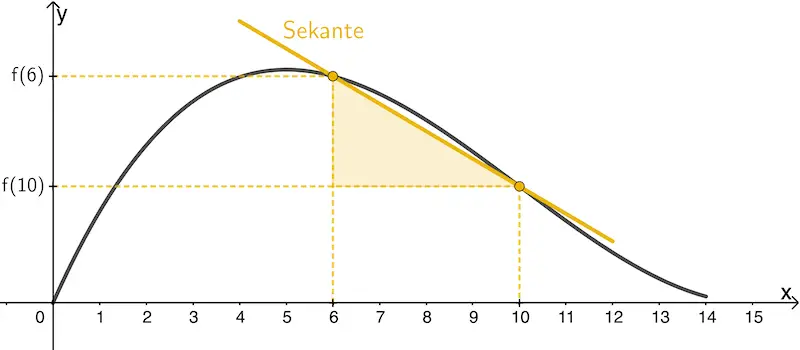
Das mittlere Gefälle der Rutsche im Intervall \([6;10]\) entspricht der mittleren Änderungsrate von \(f\) im Intervall \([6;10]\), das heißt, dem Wert des Differenzenquotienten \(\dfrac{f(10) - f(6)}{10 - 6}\).
In graphischer Interpretation ist dies die Steigung \(\textcolor{#e9b509}{m_S}\) der Sekante durch die Punkte \((6|f(6))\) und \((10|f(10))\).
Differenzenquotient oder mittlere Änderungsrate
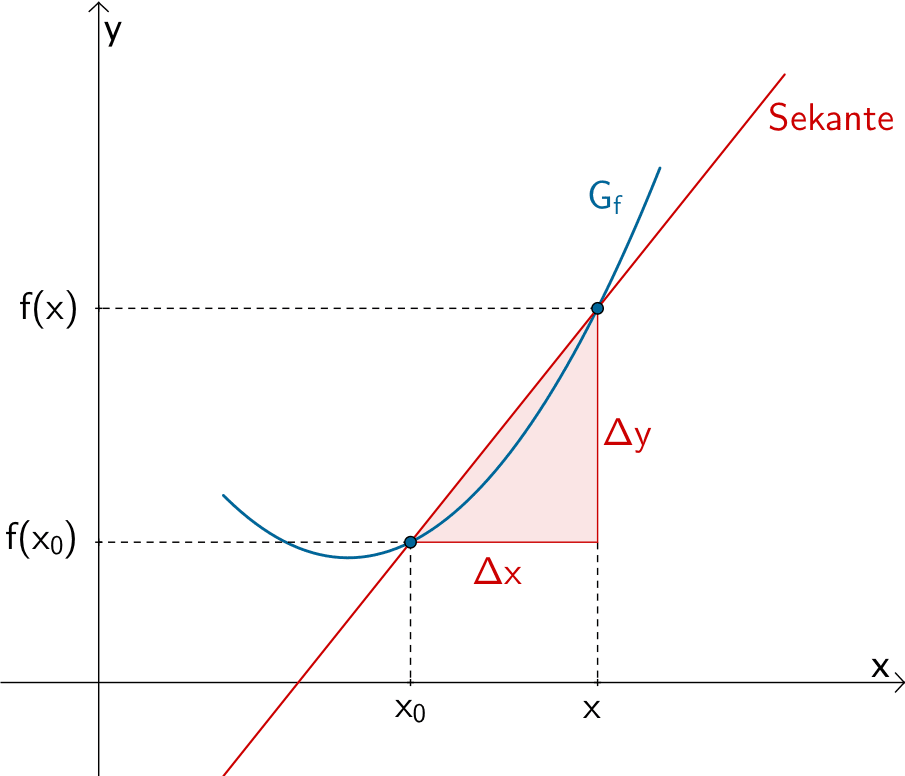
Der Differenzenquotient oder die mittlere Änderungsrate \(m_{s} = \dfrac{f(x) - f(x_{0})}{x - x_{0}}\) beschreibt die Steigung der Sekante durch den Punkt \((x_{0}|f(x_{0}))\) und einen weiteren Punkt des Graphen der Funktion \(f\).
\[f(x) = 0{,}01x^3 - 0{,}3x^2 + 2{,}25x\]
\[\begin{align*}\textcolor{#e9b509}{m_S} &= \frac{f(10) - f(6)}{10 - 6} \\[0.8em] &= \frac{0{,}01 \cdot 10^3 - 0{,}3 \cdot 10^2 + 2{,}25 \cdot 10 - (0{,}01 \cdot 6^3 - 0{,}3 \cdot 6^2 + 2{,}25 \cdot 6)}{4} \\[0.8em] &= \frac{2{,}5 - 4{,}86}{4} \\[0.8em] &= -0{,}59\end{align*}\]
Das mittlere Gefälle der Rutsche im Intervall \([6;10]\) beträgt 59 %.
c) Beschreibung der wesentlichen Schritte zur rechnerischen Ermittlung der steilste Stelle der Rutsche im Intervall \([5;14]\)
Die Wendestelle des Graphen der Funktion \(f\) im Intervall \([5;14]\) entspricht der steilsten Stelle der Rutsche.
Wendestellen(n)
Ist eine Funktion \(f\) in einem Intervall \(I =\, ]a;b[\) zweimal differenzierbar und \(x_0\) eine innere Stelle von \(I\), so gilt:
Die Stelle \(x_0\) ist genau dann eine Wendestelle von \(f\), wenn \(f''(x_0) = 0\) ist und \(f''\) an der Stelle \(x_0\) das Vorzeichen wechselt.
Wendestelle(n) und dritte Ableitung
Ist eine Funktion \(f\) in einem Intervall \(I =\, ]a;b[\) dreimal differenzierbar und \(x_0\) eine innere Stelle von \(I\), so gilt:
Die Stelle \(x_0\) ist eine Wendestelle von \(f\), wenn \(f''(x_0) = 0\) ist und \(f'''(x_0) \neq 0\) ist.
Wesentliche Schritte
- Zweite Ableitung \(f''\) bilden.
- Nullstelle von \(f''\) im Intervall \([5;14]\) berechnen.
- Vorzeichenwechsel von \(f''\) in der Umgebung der Nullstelle nachweisen oder zeigen, dass \(f'''\) an der Nullstelle ungleich null ist.

