Ermitteln Sie unter Zuhilfenahme des Tafelwerks den kleinsten symmetrischen um den Erwartungswert liegenden Bereich, in dem die Werte der Zufallsgröße \(X\) mit einer Wahrscheinlichkeit von mindestens 75 % liegen.
(5 BE)
Lösung zu Teilaufgabe 2c
\(X\): Anzahl der Bollerwagen, die von den ersten 200 Familien entliehen werden
\(n = 200\) (Länge der Bernoulli-Kette)
\(p = 0{,}15\) (Trefferwahrscheinlichkeit für das Ereignis „Familie entleiht einen Bollerwagen.")
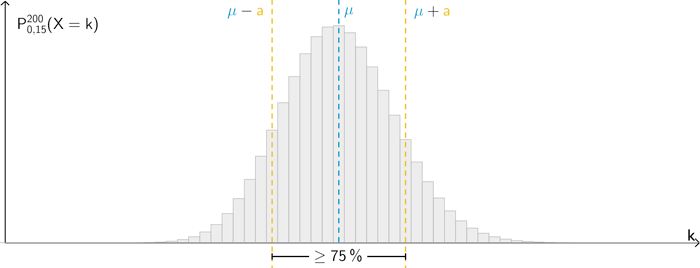
Schematische Darstellung: Kleinster symmetrisch um den Erwartungswert \(\textcolor{#0087c1}{\mu}\) liegender Bereich \(\textcolor{#0087c1}{\mu} - \textcolor{#e9b509}{a} \leq X \leq \textcolor{#0087c1}{\mu} + \textcolor{#e9b509}{a}\), in dem die Werte der Zufallsgröße \(X\) mit einer Wahrscheinlichkeit von mindestens 75 % liegen. Dabei bedeutet \(\textcolor{#e9b509}{a}\) die Abweichung vom Erwartungswert \(\textcolor{#0087c1}{\mu}\).
Es ergibt sich folgende Bedingung:
\[P_{0{,}15}^{200}(\textcolor{#0087c1}{\mu} - \textcolor{#e9b509}{a} \leq X \leq \textcolor{#0087c1}{\mu} + \textcolor{#e9b509}{a}) \geq 0{,}75\]
Erwartungswert \(\textcolor{#0087c1}{\mu} = E(X)\) der nach \(B(200;0{,}15)\) binomialverteilten Zufallsgröße \(X\) berechnen:
Erwartungswert \(\boldsymbol{\mu}\) einer binomialverteilten Zufallsgröße \(\boldsymbol{X}\)
\(\mu = E(X) = n \cdot p\) (vgl. Merkhilfe)
Wobei \(n\) die Länge der Bernoullikette und \(p\) die Trefferwahrscheinlichkeit für das Eintreten des betrachteten Ereignisses ist.
\[\textcolor{#0087c1}{\mu} = n \cdot p = 200 \cdot 0{,}15 = \textcolor{#0087c1}{30}\]
Kleinsten Bereich \(\textcolor{#0087c1}{30} - \textcolor{#e9b509}{a} \leq X \leq \textcolor{#0087c1}{30} + \textcolor{#e9b509}{a}\) mithilfe des Stochastischen Tafelwerks ermitteln:
In der Tabelle für \(p = 0{,}15\) und \(n = 200\) lässt sich mithilfe der in der rechten Spalte tabellarisierten aufsummierten Wahrscheinlichkeitswerte \(\sum \limits_{i\,=\,0}^{k}B(n;p;i)\) in etwa abschätzen, wie die Abweichung \(\textcolor{#e9b509}{a}\) vom Erwartungswert \(\textcolor{#0087c1}{\mu = 30}\) zu wählen ist, damit die Bedingung \(P_{0{,}15}^{200}(\textcolor{#0087c1}{30} - \textcolor{#e9b509}{a} \leq X \leq \textcolor{#0087c1}{30} + \textcolor{#e9b509}{a}) \geq 0{,}75\) erfüllt ist.
Für \(\textcolor{#e9b509}{a = 5}\) ergibt sich mithilfe des Stochastischen Tafelwerks (ST):
Kumulative Verteilungsfunktion einer nach \(B(n, p)\) binomialverteilten Zufallsgröße \(X\)
\[F^n_p (k) = P^n_p (X \leq k) = \sum_{i \, = \, 0}^k B(n; p; i) = \sum_{i \, = \, 0}^k \binom{n}{i} \cdot p^i \cdot (1 - p)^{n - i}\]
Wobei \(n\) die Länge der Bernoullikette, \(p\) die Trefferwahrscheinlichkeit für das Eintreten des betrachteten Ereignisses und \(k \in \{0,1,\dots,n\}\) die Anzahl der Treffer ist.
Das Stochastische Tafelwerk (ST) listet die Werte der Kumulativen Verteilungsfunktion jeweils in der rechten Spalte einer betrachteten Tabelle der Parameter \(n\) und \(p\).
\[\begin{align*}P_{0{,}15}^{200}(\textcolor{#0087c1}{\mu} - \textcolor{#e9b509}{a} \leq X \leq \textcolor{#0087c1}{\mu} + \textcolor{#e9b509}{a}) &= P_{0{,}15}^{200}(\textcolor{#0087c1}{30} - \textcolor{#e9b509}{5} \leq X \leq \textcolor{#0087c1}{30} + \textcolor{#e9b509}{5})\\[0.8em] &= P_{0{,}15}^{200}(25 \leq X \leq 35) \\[0.8em] &= P_{0{,}15}^{200}(X \leq 35) - P_{0{,}15}^{200}(X \leq 24) \\[0.8em] &= \sum \limits_{i\,=\,0}^{35}B(200;0{,}15;i) - \sum \limits_{i\,=\,0}^{24}B(200;0{,}15;i) \\[0.8em] &\overset{\text{ST}}{=} 0{,}86127 - 0{,}13682 \\[0.8em] &= 0{,}72445 \textcolor{#cc071e}{<} 0{,}75 \end{align*}\]
Mit \(P_{0{,}15}^{200}(25 \leq X \leq 35) \textcolor{#cc071e}{<} 0{,}75\) ist der Bereich \(25 \leq X \leq 35\) noch zu klein.
Für \(\textcolor{#e9b509}{a = 6}\) ergibt sich mithilfe des Stochastischen Tafelwerks (ST):
Kumulative Verteilungsfunktion einer nach \(B(n, p)\) binomialverteilten Zufallsgröße \(X\)
\[F^n_p (k) = P^n_p (X \leq k) = \sum_{i \, = \, 0}^k B(n; p; i) = \sum_{i \, = \, 0}^k \binom{n}{i} \cdot p^i \cdot (1 - p)^{n - i}\]
Wobei \(n\) die Länge der Bernoullikette, \(p\) die Trefferwahrscheinlichkeit für das Eintreten des betrachteten Ereignisses und \(k \in \{0,1,\dots,n\}\) die Anzahl der Treffer ist.
Das Stochastische Tafelwerk (ST) listet die Werte der Kumulativen Verteilungsfunktion jeweils in der rechten Spalte einer betrachteten Tabelle der Parameter \(n\) und \(p\).
\[\begin{align*}P_{0{,}15}^{200}(\textcolor{#0087c1}{\mu} - \textcolor{#e9b509}{a} \leq X \leq \textcolor{#0087c1}{\mu} + \textcolor{#e9b509}{a}) &= P_{0{,}15}^{200}(\textcolor{#0087c1}{30} - \textcolor{#e9b509}{6} \leq X \leq \textcolor{#0087c1}{30} + \textcolor{#e9b509}{6})\\[0.8em] &= P_{0{,}15}^{200}(24 \leq X \leq 36) \\[0.8em] &= P_{0{,}15}^{200}(X \leq 36) - P_{0{,}15}^{200}(X \leq 23) \\[0.8em] &= \sum \limits_{i\,=\,0}^{36}B(200;0{,}15;i) - \sum \limits_{i\,=\,0}^{23}B(200;0{,}15;i) \\[0.8em] &\overset{\text{ST}}{=} 0{,}89872 - 0{,}09592 \\[0.8em] &= 0{,}8028 \textcolor{#89ba17}{>} 0{,}75 \end{align*}\]
Somit ist \(24 \leq X \leq 36\) der kleinste symmetrisch um den Erwartungswert liegenden Bereich, in dem die Werte der Zufallsgröße \(X\) mit einer Wahrscheinlichkeit von mindestens 75 % liegen.
Anmerkung:
Es ist wichtig, beide Berechnungen für \(\textcolor{#e9b509}{a = 5}\) und \(\textcolor{#e9b509}{a = 6}\) durchzuführen. Denn nur dann ist nachgewiesen, dass sich für \(\textcolor{#e9b509}{a = 6}\) der kleinste Bereich \(24 \leq X \leq 36\) ergibt.


