Das Süßwarenunternehmen produziert auch zuckerreduzierte und vegane Fruchtgummis und bringt diese in entsprechend gekennzeichneten Tüten in den Handel.
Der Anteil der nicht als vegan gekennzeichneten Tüten ist dreimal so groß wie der Anteil der Tüten, die als vegan gekennzeichnet sind. 42 % der Tüten, die als vegan gekennzeichnet sind, sind zusätzlich auch als zuckerreduziert gekennzeichnet. Insgesamt sind 63 % der Tüten weder als vegan noch als zuckerreduziert gekennzeichnet.
Betrachtet werden folgende Ereignisse:
\(V\): „Eine zufällig ausgewählte Tüte ist als vegan gekennzeichnet."
\(R\): „Eine zufällig ausgewählte Tüte ist als zuckerreduziert gekennzeichnet."
Bestimmen Sie die Wahrscheinlichkeit des Ereignisses \(\overline{R}\).
(3 BE)
Lösung zu Teilaufgabe 3a
\(V\): „Eine zufällig ausgewählte Tüte ist als vegan gekennzeichnet."
\(R\): „Eine zufällig ausgewählte Tüte ist als zuckerreduziert gekennzeichnet."
Analyse der Angabe:
„Der Anteil der nicht als vegan gekennzeichneten Tüten ist dreimal so groß wie der Anteil der Tüten, die als vegan gekennzeichnet sind."
\[\Rightarrow \enspace P(\overline{V}) = 3 \cdot P(V)\]
„42 % der Tüten, die als vegan gekennzeichnet sind, sind zusätzlich auch als zuckerreduziert gekennzeichnet."
\[\Rightarrow \enspace P_{V}(R) = 0{,}42\]
Bedingte Wahrscheinlichkeit
Die Wahrscheinlichkeit für das Eintreten des Ereignisses \(B\) unter der Voraussetzung oder der Bedingung, dass das Ereignis \(A\) bereits eingetreten ist, heißt bedingte Wahrscheinlichkeit von \(\boldsymbol{B}\) unter der Bedingung \(\boldsymbol{A}\) und wird durch die Schreibweise \(P_{A}(B)\) gekennzeichnet.
Es gilt: \(P_{A}(B) = \dfrac{P(A \cap B)}{P(A)} \quad (P(A) \neq 0)\)
(vgl. Merkhilfe)
„Insgesamt sind 63 % der Tüten weder als vegan noch als zuckerreduziert gekennzeichnet."
\[\Rightarrow \enspace P(\overline{V} \cap \overline{R}) = 0{,}63\]
1. Möglichkeit: Baumdiagramm
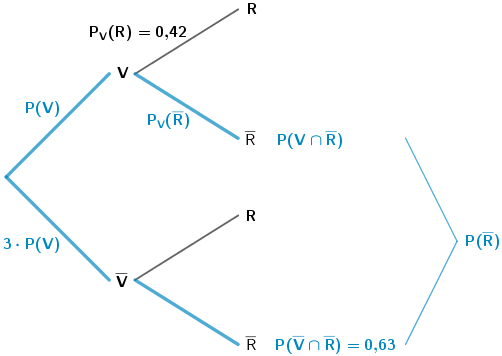
Nach der 1. bzw. 2. Pfadregel gilt:
Pfadregeln
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu diesem Ereignis gehören.
1. Pfadregel: \(\textcolor{#0087c1}{P(V \cap \overline{R})} = \textcolor{#0087c1}{P(V)} \cdot \textcolor{#0087c1}{P_{V}(\overline{R})}\)
2. Pfadregel: \(\textcolor{#0087c1}{P(\overline{R})} = \textcolor{#0087c1}{P(V \cap \overline{R})} + \textcolor{#0087c1}{P(\overline{V} \cap \overline{R})}\)
\(\textcolor{#0087c1}{P(V)}\) und \(\textcolor{#0087c1}{P_{V}(\overline{R})}\) mithilfe der Knotenregel berechnen:
Pfadregeln
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu diesem Ereignis gehören.
\[\begin{align*}P(V) + P(\overline{V}) &= 1 \\[0.8em] P(V) + 3 \cdot P(V) &= 1\\[0.8em]4 \cdot P(V) &= 1 &&| : 4 \\[0.8em] \textcolor{#0087c1}{P(V)} &= \textcolor{#0087c1}{0{,}25}\end{align*}\]
\[\begin{align*} P_{V}(R) + P_{V}(\overline{R}) &= 1 &&| - P_{V}(R)\\[0.8em] P_{V}(\overline{R}) &= 1 - P_{V}(R) \\[0.8em] P_{V}(\overline{R})&= 1 - 0{,}42 \\[0.8em] \textcolor{#0087c1}{P_{V}(\overline{R})}&= \textcolor{#0087c1}{0{,}58} \end{align*}\]
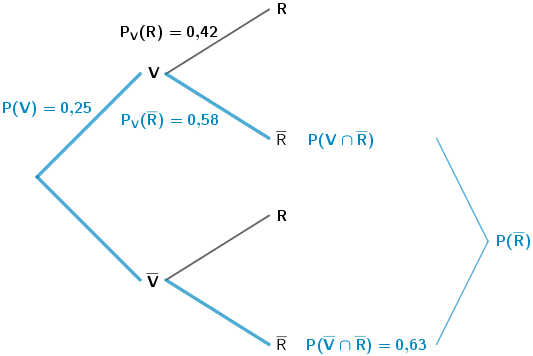
Wahrscheinlichkeit \(P(\overline{R})\) berechnen:
Pfadregeln
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu diesem Ereignis gehören.
\[\begin{align*}\textcolor{#0087c1}{P(\overline{R})} &= \textcolor{#0087c1}{P(V \cap \overline{R})} + \textcolor{#0087c1}{P(\overline{V} \cap \overline{R})} \\[0.8em] &= \underbrace{\underbrace{P(V) \cdot P_{V}(\overline{R})}_{\text{1. Pfadregel}} + P(\overline{V}\cap \overline{R})}_{\text{2. Pfadregel}} \\[0.8em] &=\textcolor{#0087c1}{0{,}25} \cdot \textcolor{#0087c1}{0{,}58}+ \textcolor{#0087c1}{0{,}63} \\[0.8em] &= 0{,}775\end{align*}\]
2. Möglichkeit: Vierfeldertafel (der Wahrscheinlichkeiten)
\[\textcolor{#0087c1}{P(\overline{V})} = \textcolor{#0087c1}{3 \cdot P(V)}\]
\(P_{V}(R) = 0{,}42\) (Kann nicht in die Vierfeldertafel eingetragen werden.)
\[\textcolor{#0087c1}{P(\overline{V} \cap \overline{R})} = \textcolor{#0087c1}{0{,}63}\]
| \(V\) | \(\overline{V}\) | ||
| \(R\) | \(\textcolor{#e9b509}{P(V \cap R)}\) | ||
| \(\overline{R}\) | \(\) | \(\textcolor{#0087c1}{0{,}63}\) | |
| \(\textcolor{#0087c1}{P(V)}\) | \(\textcolor{#0087c1}{3 \cdot P(V)}\) | \(1\) |
Um mit der Vierfeldertafel arbeiten zu können, wird zunächst \(\textcolor{#0087c1}{P(V)}\) und \(\textcolor{#e9b509}{P(V\cap R)}\) berechnet.
\[\begin{align*}P(V) + P(\overline{V}) &= 1 \\[0.8em] \textcolor{#0087c1}{P(V)} + \textcolor{#0087c1}{3 \cdot P(V)} &= 1\\[0.8em]4 \cdot P(V) &= 1 &&| : 4 \\[0.8em] \textcolor{#0087c1}{P(V)} &= \textcolor{#0087c1}{0{,}25}\end{align*}\]
Bedingte Wahrscheinlichkeit
Die Wahrscheinlichkeit für das Eintreten des Ereignisses \(B\) unter der Voraussetzung oder der Bedingung, dass das Ereignis \(A\) bereits eingetreten ist, heißt bedingte Wahrscheinlichkeit von \(\boldsymbol{B}\) unter der Bedingung \(\boldsymbol{A}\) und wird durch die Schreibweise \(P_{A}(B)\) gekennzeichnet.
Es gilt: \(P_{A}(B) = \dfrac{P(A \cap B)}{P(A)} \quad (P(A) \neq 0)\)
(vgl. Merkhilfe)
\[\begin{align*} P_{V}(R) = \frac{\textcolor{#e9b509}{P(V \cap R)}}{\textcolor{#0087c1}{P(V)}} &= 0{,}42 &&| \cdot P(V) \\[0.8em] \textcolor{#e9b509}{P(V \cap R)} &= 0{,}42 \cdot \textcolor{#0087c1}{P(V)} \\[0.8em] \textcolor{#e9b509}{P(V \cap R)} &= 0{,}42 \cdot \textcolor{#0087c1}{0{,}25} \\[0.8em] &= \textcolor{#e9b509}{0{,}105} \end{align*}\]
| \(V\) | \(\overline{V}\) | ||
| \(R\) | \(\textcolor{#e9b509}{0{,}105}\) | ||
| \(\overline{R}\) | \(\textcolor{#0087c1}{0{,}63}\) | ||
| \(\textcolor{#0087c1}{0{,}25}\) | \(\textcolor{#0087c1}{0{,}75}\) | \(1\) |
Durch spalten- bzw. zeilenweises Subtrahieren bzw. Addieren ergibt sich:
\[P(V \cap \overline{R}) = \textcolor{#0087c1}{P(V)} - \textcolor{#e9b509}{P(V \cap R)} = \textcolor{#0087c1}{0{,}25} - \textcolor{#e9b509}{0{,}105} = 0{,}145\]
| \(V\) | \(\overline{V}\) | ||
| \(R\) | \(0{,}105\) | ||
| \(\overline{R}\) | \(0{,}145\) | \(\textcolor{#0087c1}{0{,}63}\) | |
| \(\textcolor{#0087c1}{0{,}25}\) | \(\textcolor{#0087c1}{0{,}75}\) | \(1\) |
\[P(\overline{R}) = P(V \cap \overline{R}) + \textcolor{#0087c1}{P(\overline{V}\cap\overline{R})} = 0{,}145 + \textcolor{#0087c1}{0{,}63} = 0{,}775\]
| \(V\) | \(\overline{V}\) | ||
| \(R\) | \(0{,}105\) | ||
| \(\overline{R}\) | \(0{,}145\) | \(\textcolor{#0087c1}{0{,}63}\) | \(0{,}775\) |
| \(\textcolor{#0087c1}{0{,}25}\) | \(\textcolor{#0087c1}{0{,}75}\) | \(1\) |


