Der Schattenbereich der gesamten Pyramide auf dem Boden besteht im Modell aus zwei kongruenten Vierecken. Zeichnen Sie diesen Schattenbereich in Abbildung 3 ein und geben Sie die besondere Form der genannten Vierecke an.
(4 BE)
Lösung zu Teilaufgabe g
Abb. 3
Die beiden Vierecke sind Trapeze.
Ausführliche Lösung (nicht verlangt)
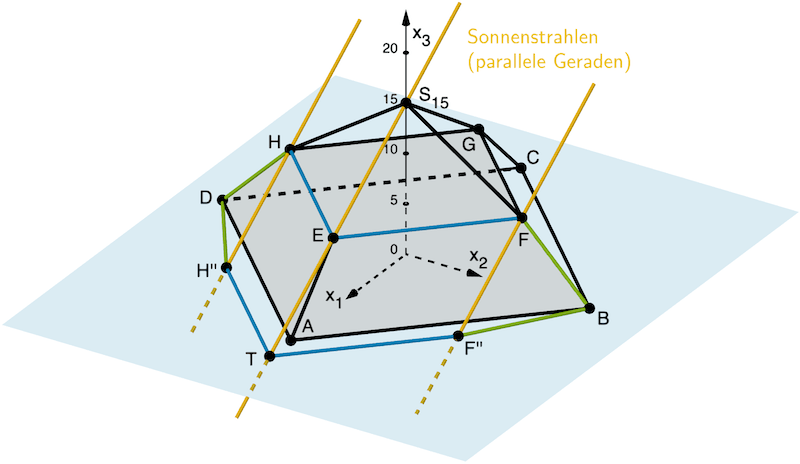
Die Schattenlinien der zu den Grundkanten \([AB]\) bzw. \([AD]\) parallel verlaufenden Kanten \(\textcolor{#0087c1}{[EF]}\) bzw. \(\textcolor{#0087c1}{[EH]}\) werden durch die parallel einfallenden Lichtstrahlen parallel abgebildet.
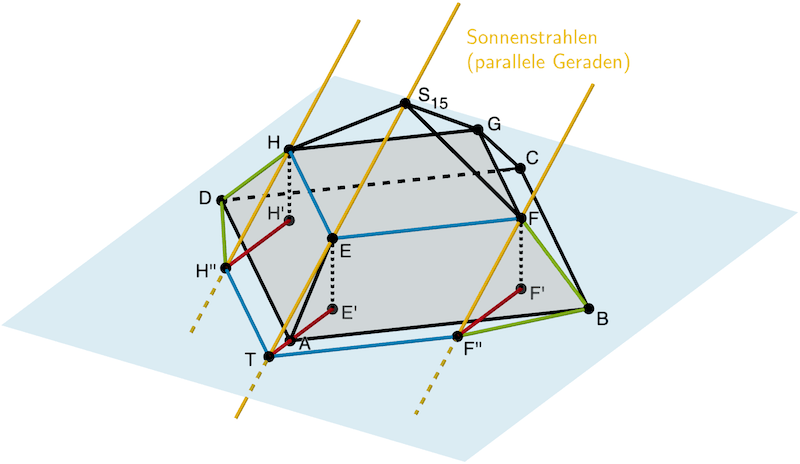
Die Schattenpunkte \(T\), \(F''\) und \(H''\) der Eckpunkte \(E\), \(F\) und \(H\) haben von den Lotfußpunkten \(E'\), \(F'\) und \(H'\) des Lotes der Punkte \(E\), \(F\) und \(H\) auf die \(x_1x_2\)-Ebene jeweils den gleichen Abstand.
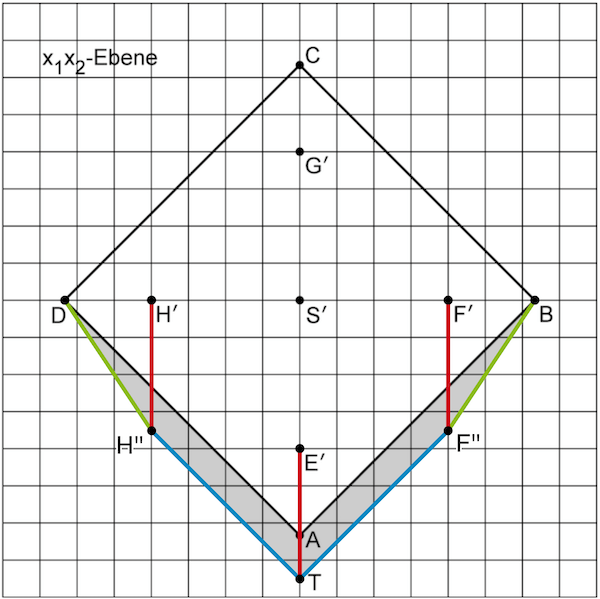Abb. 3
Der Schattenpunkt \(T\) des Eckpunkts \(E\) ist vom Lotfußpunkt \(E'\) ca. 3,5 Kästchen entfernt. Überträgt man diesen Abstand auf \(F'\) bzw. \(H'\) in gleicher Richtung, so erhält man die Schattenpunkte \(F''\) bzw. \(H''\) der Eckpunkte \(F\) und \(H\).
Die Schattenlinien der schrägen Kanten \(\textcolor{#89ba17}{[BF]}\) bzw. \(\textcolor{#89ba17}{[DH]}\) sind die Strecken \(\textcolor{#89ba17}{[BF'']}\) bzw. \(\textcolor{#89ba17}{[DH'']}\), wobei \(B\) und \(D\) die Punkte in der \(x_1x_2\)-Ebene sind, bei denen der Schatten beginnt.
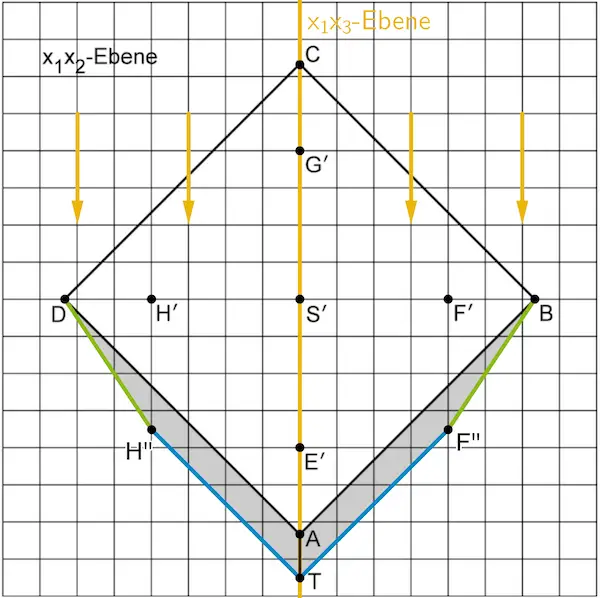Abb. 3
Da die Schattenlinien \(\textcolor{#0087c1}{[TF'']}\) bzw. \(\textcolor{#0087c1}{[TH'']}\) der Kanten \([EF]\) bzw. \([EH]\) parallel zu den Grundkanten \(\boldsymbol{[AB]}\) bzw. \(\boldsymbol{[AD]}\) abgebildet werden, sind die Vierecke \(ATF''B\) und \(DH''TA\) Trapeze.
Der Lichteinfall erfolgt im Modell parallel zur \(\textcolor{#e9b509}{x_1x_3}\)-Ebene, welche Symmetrieebene des Körpers \(ABCDEFGHS_{15}\) (Knickpyramide) ist. Daher sind die beiden Trapeze zueinander kongruent.
