Berechnen Sie den Inhalt der Fläche, die \(G_f\) mit den Koordinatenachsen und der Geraden \(x = 4\) einschließt.
(4 BE)
Lösung zu Teilaufgabe 1e
Flächeninhaltsberechnung durch Integration
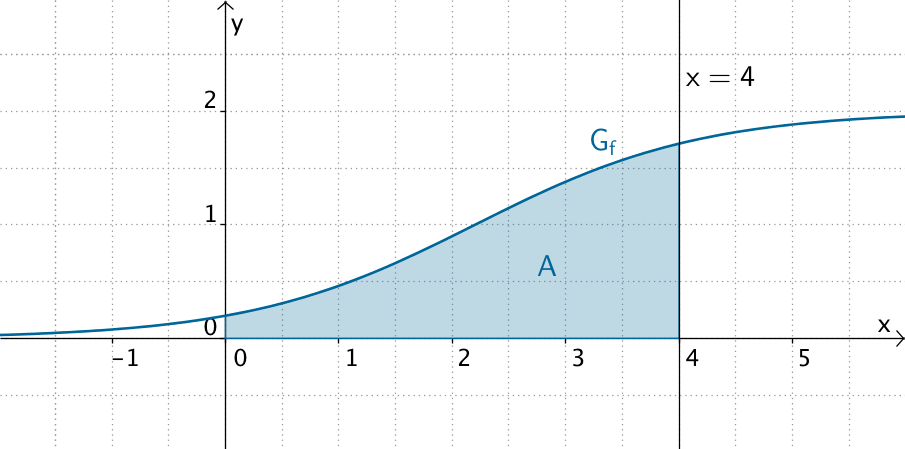
Fläche, die \(\,G_f\,\) mit den Koordinatenachsen und der Geraden \(\,x = 4\,\) einschließt
Der Flächeninhalt \(A\) des Flächenstücks, das der Graph von \(f\) mit den Koordinatenachsen und der Geraden \(x = 4\) einschließt, ist gleich dem Wert des bestimmten Integrals \(\int_{0}^{4} f(x)\,dx\,\).
\[A = \int_{0}^{4} f(x)\,dx\]
Berechnung bestimmter Integrale
\[\int_{a}^{b} f(x)\,dx = [F(x)]_{a}^{b} = F(b) - F(a)\]
Dabei ist \(F\) eine beliebige Stammfunktion zu \(f\).
(vgl. Merkhilfe)
Eigenschaften des bestimmten Integrals - Integrationsregeln
Identische Integrationsgrenzen:
\[\int_{a}^{a} f(x)\,dx = 0\]
Faktorregel:
\(\displaystyle \int_{a}^{b} c \cdot f(x)\,dx = c \cdot \int_{a}^{b} f(x)\,dx\) mit \(c \in \mathbb R\)
Summenregel:
\[\int_{a}^{b} \left[f(x) \pm g(x) \right] dx = \int_{a}^{b}f(x)\,dx \pm \int_{a}^{b}g(x)\,dx\]
Vertauschungsregel:
\[\int_{a}^{b}f(x)\,dx = -\int_{b}^{a}f(x)\,dx\]
Zerlegung in Teilintervalle:
\(\displaystyle \int_{a}^{b}f(x)\,dx = \int_{a}^{c}f(x)\,dx + \int_{c}^{b}f(x)\,dx\) mit \(a \leq c \leq b\)
Stammfunktion \(F(x)\) von \(f(x)\) bestimmen:
\[f(x) = \frac{2e^x}{e^x + 9} = 2 \cdot \frac{e^x}{e^x + 9}\]
Die Quotientenfunktion \(f\) hat die Form \(\displaystyle 2 \cdot \frac{g'(x)}{g(x)}\,\) mit \(\,g(x) = e^x + 9\,\) und \(\,g'(x) = e^x\,\).
Ableitung der natürlichen Exponentialfunktion
\[f(x) = e^x \quad \Longrightarrow \quad f'(x) = e^x\]
(vgl. Merkhilfe)
\[(e^x + 9)' = e^x\]
Wichtiges unbestimmtes Integral:
\[\int \frac{f'(x)}{f(x)}dx = \ln \vert f(x) \vert + C\]
(vgl. Merkhilfe)
\[f(x) = \frac{2e^x}{e^x + 9} \quad \Longrightarrow \quad F(x) = 2 \cdot \ln(e^x + 9) + C\]
Flächeninhalt \(A\) berechnen:
\[\begin{align*} A &= \int_{0}^{4} f(x)\,dx \\[0.8em] &= \big[ 2 \cdot \ln(e^x + 9) \big]_{0}^{4} \\[0.8em] &= 2 \cdot \ln\big(e^4 + 9\big) - \left( 2 \cdot \ln\big(e^0 + 9\big) \right) \\[0.8em] &= 2 \cdot \ln\bigg( \frac{e^4 + 9}{10} \bigg) \\[0.8em] &\approx 3{,}7 \end{align*}\]
Der Inhalt der Fläche, die \(G_f\) mit den Koordinatenachsen und der Geraden \(x = 4\) einschließt, beträgt ca. 3,7 FE (Flächeneinheiten).


