G9 Mathematik Klausur Q11/2-005 Bayern

Aufgabe 1

Bestimmen Sie die Ableitung der Funktion \(f\)mit \(f(x) = 0{,}5x^2 + 3x\) an der Stelle \(x = -2\) mithilfe des Differentialquotienten. Tipp: Verwenden Sie die h-Methode.

Aufgabe 2

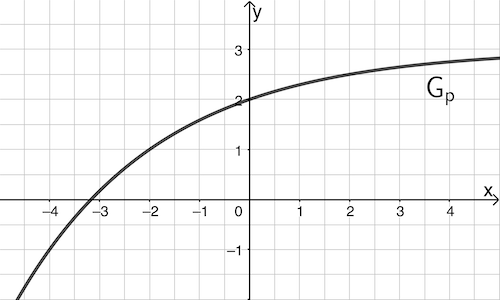
Die Abbildung zeigt den Graphen einer Funktion \(p\).

a) Bestimmen Sie mithilfe der Abbildung die mittlere Änderungsrate von \(p\) im Intervall \([-2;2]\) und veranschaulichen Sie Ihre Vorgehensweise durch geeignete Eintragungen in die Abbildung. Entscheiden Sie, ob es im dargestellten Bereich des Graphen \(G_p\) ein Intervall gibt, in dem die mittlere Änderungsrate von \(p\) kleiner als null ist. Begründen Sie Ihre Entscheidung kurz.

b) Erklären Sie die Bedeutung des Grenzwerts \(\lim \limits_{x\,\to\,-2}\dfrac{p(x) - p(-2)}{x + 2}\). Veranschaulichen Sie diesen in der Abbildung und bestimmen Sie damit näherungsweise den Grenzwert.

Aufgabe 3

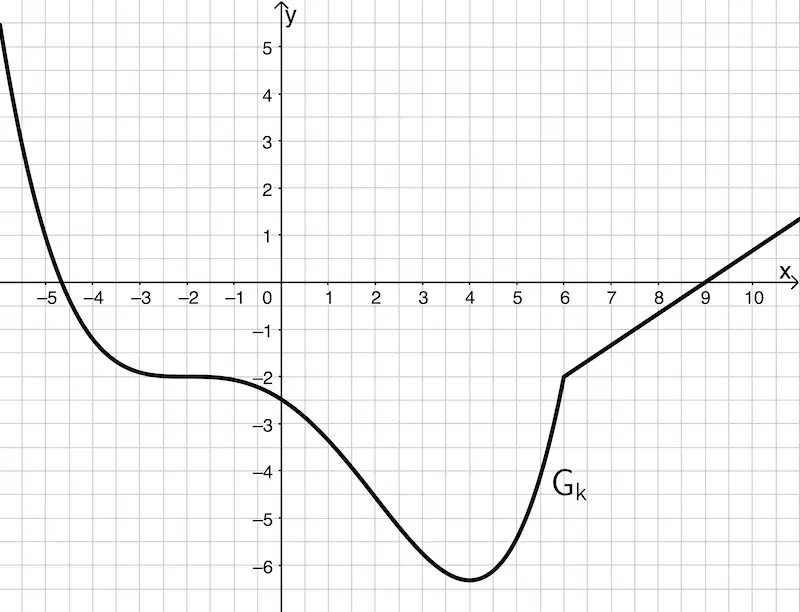
Die Abbildung zeigt den Graphen \(G_k\) einer Funktion \(k\).

a) Begründen Sie, dass \(k\) an der Stelle \(x = 6\) nicht differenzierbar ist, indem Sie mithilfe der Abbildung zugehörige Grenzwerte angeben und daraus schlussfolgern.

b) Skizzieren Sie in der Abbildung den Graphen der Ableitungsfunktion \(k'\). Achten Sie auf ausreichende Genauigkeit.

Aufgabe 4

Die Tangente an den Graphen der Funktion \(f\) mit \(f(x) = 0{,}5x^2\) im Punkt \(P(2|f(2))\) und die Normale bilden mit der \(x\)-Achse das Dreieck \(PQR\).

a) Veranschaulichen Sie den Sachverhalt in einer Skizze.

b) Berechnen Sie den Flächeninhalt sowie die Innenwinkel des Dreiecks.

Aufgabe 5

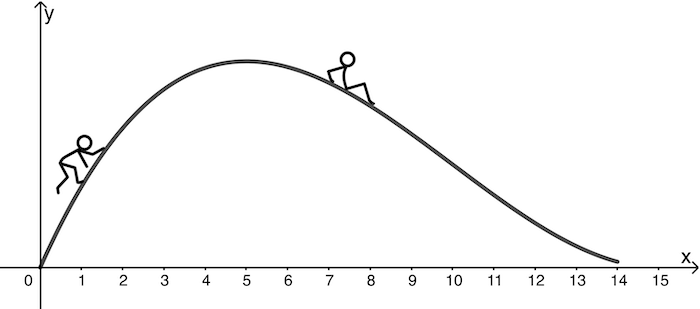
Die Abbildung zeigt modellhaft den Verlauf einer Wasserrutsche, der näherungsweise durch die Funktion \(f \colon x \mapsto 0{,}01x^3 -0{,}3x^2 + 2{,}25x\) mit \(D_f = [0:14]\) beschrieben wird. Eine Längeneinheit im Koordinatensystem entspricht 0,5 m in der Realität.

a) Bestimmen Sie die maximale Höhe der Rutsche durch Rechnung.

b) Berechnen Sie das mittlere Gefälle der Rutsche im Intervall \([6;10]\).

c) Beschreiben Sie die wesentlichen Schritte, um die steilste Stelle der Rutsche im Intervall \([5;14]\) rechnerisch zu ermitteln.

Aufgabe 6

Die Graphen der Funktionen \(f \colon x \mapsto 0{,}5x^2 - 3x + 4\) und \(g \colon x \mapsto x^3 - x+1\) besitzen genau einen gemeinsamen Punkt. Berechnen Sie die \(x\)-Koordinate dieses Punktes mit dem Newton-Verfahren auf zwei Dezimalen genau. Wählen Sie als Startwert \(x_0 = 1\).

(Zur Kontrolle: \(x\)-Koordinate des gemeinsamen Punktes: \(\approx 1{,}11617\))

Bestimmen Sie die Ableitung der Funktion \(f\)mit \(f(x) = 0{,}5x^2 + 3x\) an der Stelle \(x = -2\) mithilfe des Differentialquotienten. Tipp: Verwenden Sie die h-Methode.

Die Abbildung zeigt den Graphen einer Funktion \(p\).

a) Bestimmen Sie mithilfe der Abbildung die mittlere Änderungsrate von \(p\) im Intervall \([-2;2]\) und veranschaulichen Sie Ihre Vorgehensweise durch geeignete Eintragungen in die Abbildung. Entscheiden Sie, ob es im dargestellten Bereich des Graphen \(G_p\) ein Intervall gibt, in dem die mittlere Änderungsrate von \(p\) kleiner als null ist. Begründen Sie Ihre Entscheidung kurz.

b) Erklären Sie die Bedeutung des Grenzwerts \(\lim \limits_{x\,\to\,-2}\dfrac{p(x) - p(-2)}{x + 2}\). Veranschaulichen Sie diesen in der Abbildung und bestimmen Sie damit näherungsweise den Grenzwert.

Die Abbildung zeigt den Graphen \(G_k\) einer Funktion \(k\).

a) Begründen Sie, dass \(k\) an der Stelle \(x = 6\) nicht differenzierbar ist, indem Sie mithilfe der Abbildung zugehörige Grenzwerte angeben und daraus schlussfolgern.

b) Skizzieren Sie in der Abbildung den Graphen der Ableitungsfunktion \(k'\). Achten Sie auf ausreichende Genauigkeit.

Die Tangente an den Graphen der Funktion \(f\) mit \(f(x) = 0{,}5x^2\) im Punkt \(P(2|f(2))\) und die Normale bilden mit der \(x\)-Achse das Dreieck \(PQR\).

a) Veranschaulichen Sie den Sachverhalt in einer Skizze.

b) Berechnen Sie den Flächeninhalt sowie die Innenwinkel des Dreiecks.

Die Abbildung zeigt modellhaft den Verlauf einer Wasserrutsche, der näherungsweise durch die Funktion \(f \colon x \mapsto 0{,}01x^3 -0{,}3x^2 + 2{,}25x\) mit \(D_f = [0:14]\) beschrieben wird. Eine Längeneinheit im Koordinatensystem entspricht 0,5 m in der Realität.

a) Bestimmen Sie die maximale Höhe der Rutsche durch Rechnung.

b) Berechnen Sie das mittlere Gefälle der Rutsche im Intervall \([6;10]\).

c) Beschreiben Sie die wesentlichen Schritte, um die steilste Stelle der Rutsche im Intervall \([5;14]\) rechnerisch zu ermitteln.

Die Graphen der Funktionen \(f \colon x \mapsto 0{,}5x^2 - 3x + 4\) und \(g \colon x \mapsto x^3 - x+1\) besitzen genau einen gemeinsamen Punkt. Berechnen Sie die \(x\)-Koordinate dieses Punktes mit dem Newton-Verfahren auf zwei Dezimalen genau. Wählen Sie als Startwert \(x_0 = 1\).

(Zur Kontrolle: \(x\)-Koordinate des gemeinsamen Punktes: \(\approx 1{,}11617\))