Betrachtet werden für \(k \in \mathbb R\) die in \(]-\infty;0]\) definierten Funktionen \(f_k \colon x \mapsto f(x) + k\). Somit gilt \(f_0(x) = f(x)\), wobei sich \(f_0\) und \(f\) im Definitionsbereich unterscheiden.
Begründen Sie mithilfe der ersten Ableitung von \(\boldsymbol{f_k}\), dass \(f_k\) für jeden Wert von \(k\) umkehrbar ist. Skizzieren Sie in Abbildung 1 den Graphen der Umkehrfunktion von \(f_0\).
(4 BE)
Lösung zu Teilaufgabe 1g
\[f(x) = 2e^{-\frac{1}{8}x^2}\]
\[f_k(x) = f(x) + k; \; D_{f_k} = \;]-\infty;0], \; k \in \mathbb R\]
Begründung der Umkehrbarkeit von \(f_k\) mithilfe der ersten Ableitung von \(f_k\)
Da die Ableitung des Parameters \(k\) null ist, folgt:
\(f'_k(x) = f'(x) = -\frac{1}{2}x \cdot e^{-\frac{1}{8}x^2}\) (vgl. Teilaufgabe b)
Kriterien für die Umkehrbarkeit einer Funktion
Eine Funktion \(f\,\colon\,\mapsto f(x)\) mit der Definitionsmenge \(D_{f}\) und der Wertemenge \(W_{f}\) heißt umkehrbar, falls es zu jedem \(y \in W_{f}\) genau ein \(x \in D_{f}\) mit \(f(x) = y\) gibt.
Ist eine Funktion auf Ihrer Definitionsmenge oder einer Teilmenge streng monoton (steigend oder fallend), so ist sie dort umkehrbar.
Für alle \(x \in \; ]-\infty;0[\) gilt:
\(f'_k(x) = \underbrace{-\frac{1}{2}x}_{>\,0} \cdot \underbrace{e^{-\frac{1}{8}x^2}}_{>\,0} > 0\)
Anwendung der Differetialrechnung:
Monotoniekriterium
\(f'(x) < 0\) im Intervall \( I \enspace \Rightarrow \enspace G_{f}\) fällt streng monoton in \(I\)
\(f'(x) > 0\) im Intervall \( I \enspace \Rightarrow \enspace G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
Folglich ist \(f_k\) für alle \(x \in \; ]-\infty;0[\) streng monoton zunehmend.
Für \(x = 0\) gilt \(f'_k(0) = 0\).
Da \(f(0) > f(x)\) für \(x < 0\) gilt, ist \(\boldsymbol{f_k}\) im Definitionsbereich \(\boldsymbol{x \in \; ]-\infty;0]}\) streng monoton zunehmend und deshalb für jeden Wert von \(\boldsymbol{k}\) umkehrbar.
Skizze des Graphen der Umkehrfunktion von \(f_0\)
Umkehrfunktion \(\boldsymbol{f^{-1}}\) einer Funktion \(\boldsymbol{f}\)
Bestimmung des Funktionsterms \(\boldsymbol{f^{-1}(x)}\)
1. Funktionsgleichung \(\,y = f(x)\,\) nach \(\,x\,\) auflösen
2. Variablen tauschen: \(\;x \longleftrightarrow y \quad \Longrightarrow \quad y = f^{-1}(x)\)
Es gilt: \(\;D_{f^{-1}} = W_f\;\) und \(\; W_{f^{-1}} = D_f\)
Graph der Umkehrfunktion
Die Graphen einer Funktion und ihrer Umkehrfunktion sind zueinander symmetrisch bzgl. der Winkelhalbierenden des I. und III. Quadranten mit der Gleichung \(y = x\).
Erläuterung (nicht verlangt): Der Graph der Umkehrfunktion von \(f_0\) geht durch Spiegelung des Graphen von \(f_0\) an der Winkelhalbierenden des I. und III. Quadranten mit der Gleichung \(y = x\) hervor. Für eine möglichst genaue Skizze empfiehlt es sich, mehrerer ausgewählte Punkte des Graphen von \(f_0\) zu spiegeln.
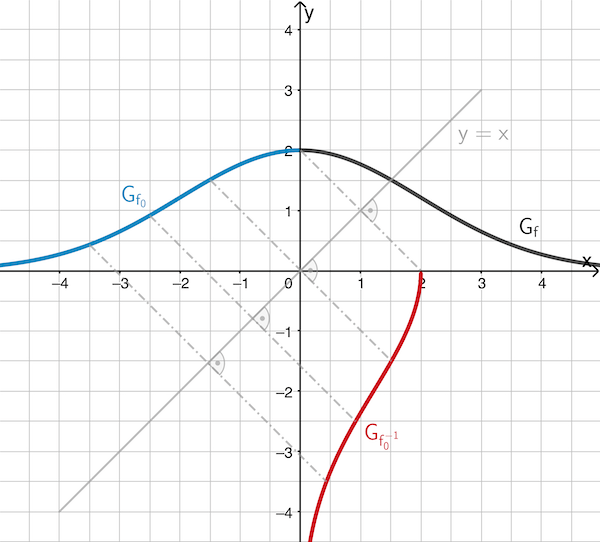Abb. 1
Graph der Funktion \(\textcolor{#0087c1}{f_0}\) und Graph der Umkehrfunktion von \(f_0\)
