Auf der Deckfläche des Grundkörpers liegt eine Stahlkugel mit einem Radius von 0,8 m. Im Modell berührt die Kugel die Deckfläche des Spats im Punkt \(K\). Beschreiben Sie, wie man im Modell rechnerisch überprüfen könnte, ob die Stahlkugel die Stange berührt, wenn die Koordinaten von \(K\) bekannt wären.
(4 BE)
Lösung zu Teilaufgabe h
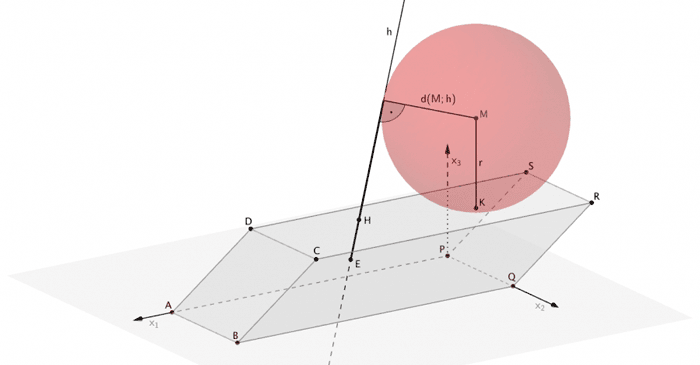
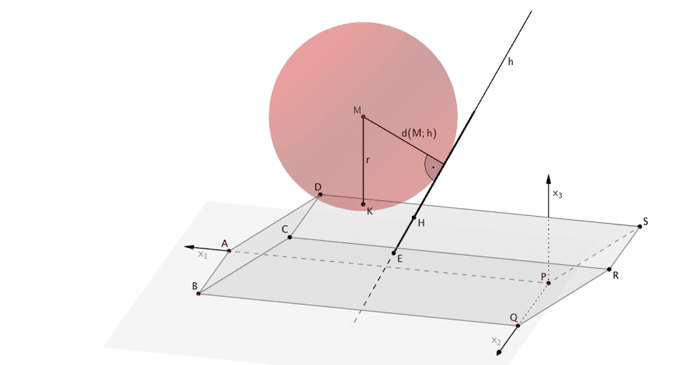
Die Stahlkugel berührt die Stange, wenn der Abstand des Mittelpunktes \(M\) der Kugel von der Geraden \(h\) gleich dem Radius \(r\) der Kugel ist.
\[d\,(M;h) = r = 0{,}8\,\text{m}\,; \quad 0{,}8\,\text{m} \, \mathrel{\widehat{=}} 8\,\text{LE} \]
A) Mittelpunkt \(M\) der Kugel bestimmen:
Man erhält die Koordinaten des Mittelpunktes \(M\) der Kugel, indem man den Punkt \(K\) um \(r = 8\) in Richtung der \(x_3\)-Achse verschiebt.
\[\overrightarrow{K} = \begin{pmatrix} x_{1_K} \\ x_{2_K} \\ 6 \end{pmatrix} \quad \Longrightarrow \quad \overrightarrow{M} = \begin{pmatrix} x_{1_K} \\ x_{2_K} \\ 6 + r \end{pmatrix} = \begin{pmatrix} x_{1_K} \\ x_{2_K} \\ 14 \end{pmatrix}\]
B) Abstand \(d\,(M;h)\) berechnen:
Ergänzung
Nachfolgend werden drei mögliche Lösungsansätze für die Berechnung des Abstands \(d\,(M;h)\) grafisch kurz erläutert.
1. Lösungsansatz: Hilfsebene
Abstand Punkt - Gerade, Ansatz: Hilfsebene aufstellen
\[P\,(p_1|p_2|p_3)\,, \quad g \colon \overrightarrow X = \overrightarrow A + \lambda \cdot \overrightarrow u\,; \quad \lambda \in \mathbb R\]
1. Hilfsebene \(H\) mit den Eigenschaften \(P \in H\) und \(H \perp g\) bestimmen:
\[H \colon \overrightarrow{n}_H \circ \left( \overrightarrow X - \overrightarrow P \right) = 0\,; \quad \overrightarrow{n}_H = \overrightarrow u\]
2. Schnittpunkt \(S\) der Ebene \(H\) mit der Geraden \(g\) ermitteln:
\(H \cap g \colon \overrightarrow{n}_H \circ \left( \overrightarrow A + \lambda \cdot \overrightarrow u - \overrightarrow P \right) = 0 \quad \Longrightarrow \quad\) Wert für Parameter \(\lambda\)
\[S \in g \colon \overrightarrow S = \overrightarrow A + \lambda \cdot \overrightarrow u\]
3. Länge der Strecke \([PS]\) berechnen:
\[d\,(P; g) = \overline{PS} = \vert \overrightarrow P - \overrightarrow S \vert\]
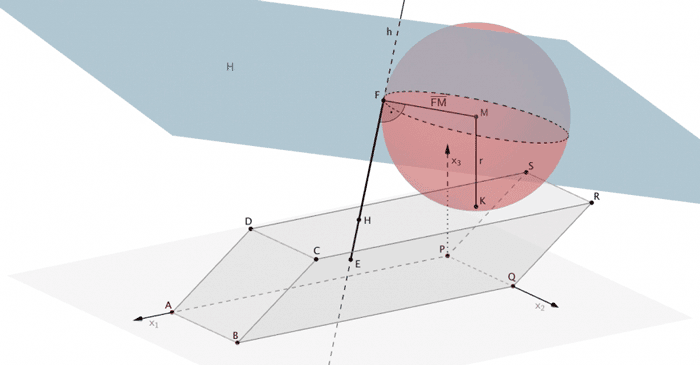
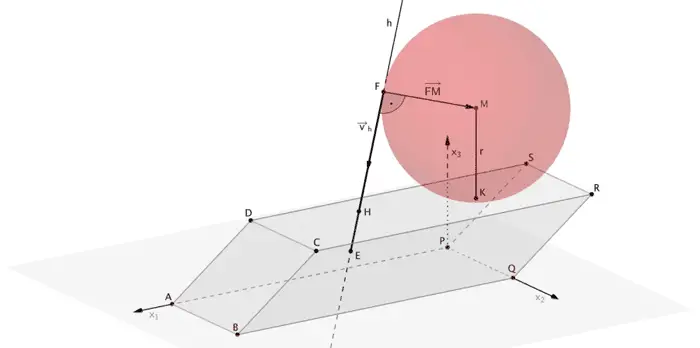
Die Hilfsebene \(H\) mit den Eigenschaften \(M \in H\) und \(h \perp H\) schneidet die Gerade \(h\) im Lotfußpunkt \(F\) des Lotes des Mittelpunktes \(M\) der Kugel auf die Gerade \(h\).
\[ h \cap H \quad \Longrightarrow \quad \overrightarrow{F}\]
\[d\,(M;h) = \overline{FM} = \vert \overrightarrow{FM} \vert\]
2. Lösungsansatz: Anwenden des Skalarprodukts
Abstand Punkt - Gerade, Ansatz: Skalarprodukt anwenden
\[P\,(p_1|p_2|p_3)\,, \quad g \colon \overrightarrow X = \overrightarrow A + \lambda \cdot \overrightarrow u\,; \quad \lambda \in \mathbb R\]
Es sei \(F\) der Lotfußpunkt des Lotes des Punktes \(P\) auf die Gerade \(g\).
Somit gilt: \(\enspace \overrightarrow{FP} \perp \overrightarrow{u} \quad \Longleftrightarrow \quad \overrightarrow{FP} \circ \overrightarrow{u} = 0\)
1. Verbindungsvektor \(\overrightarrow{FP}\) allgemein beschreiben:
\[F \in g \colon \overrightarrow F = \overrightarrow A + \lambda \cdot \overrightarrow u \quad \Longrightarrow \quad \overrightarrow{FP} = \overrightarrow P - \left( \overrightarrow A + \lambda \cdot \overrightarrow u \right) \]
2. Koordinaten des Lotfußpunktes \(F\) bestimmen:
\[\overrightarrow{FP} \circ \overrightarrow{u} = 0 \quad \Longleftrightarrow \quad \left[ \overrightarrow P - \left( \overrightarrow A + \lambda \cdot \overrightarrow u \right) \right] \circ \overrightarrow u = 0\]
\(\Longrightarrow \quad\) Wert für Parameter \(\lambda\)
\[F \in g \colon \overrightarrow F = \overrightarrow A + \lambda \cdot \overrightarrow u\]
3. Länge der Strecke \([FP]\) berechnen:
\[d\,(P;g) = \overline{FP} = \vert \overrightarrow P - \overrightarrow F \vert\]
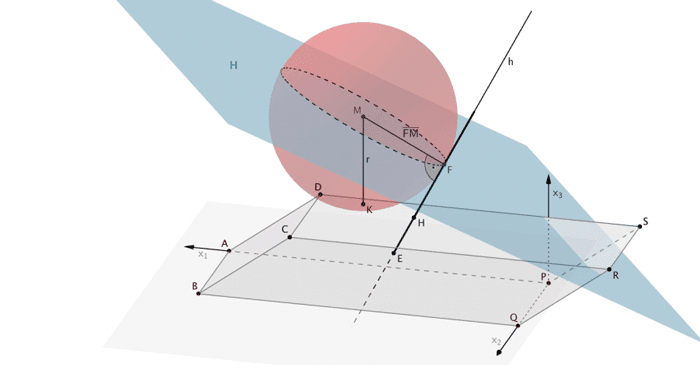
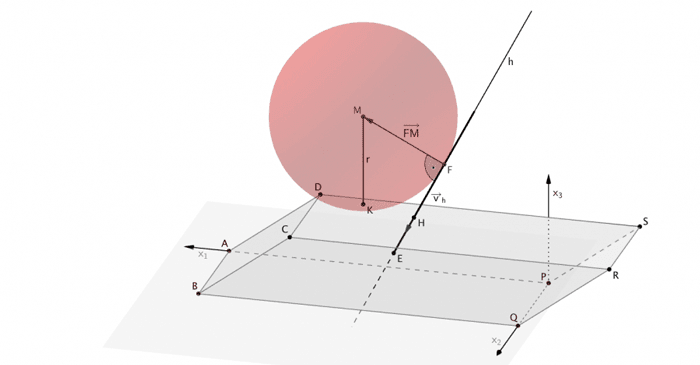
Lotfußpunkt \(F\) des Lotes des Mittelpunktes \(M\) der Kugel auf die Gerade \(h\), Orthogonale Vektoren: Richtungsvektor \(\overrightarrow{v}_h\) der Geraden \(h\) und Vektor \(\overrightarrow{FM}\)
\[F \in h\]
\[\overrightarrow{v}_h \circ \overrightarrow{FM} \overset{!}{=} 0 \quad \Longrightarrow \quad \overrightarrow{FM}\]
\[d\,(M;h) = \vert \overrightarrow{FM} \vert\]
3. Lösungsansatz: Anwenden der Differentialrechnung
Abstand Punkt - Gerade, Ansatz: Differentialrechnung anwenden
\[P\,(p_1|p_2|p_3)\,, \quad g \colon \overrightarrow X = \overrightarrow A + \lambda \cdot \overrightarrow u\,; \quad \lambda \in \mathbb R\]
1. Länge der Strecke \([PX]\) zwischen dem Punkt \(P\) und einem beliebigen Punkt \(X \in g\) beschreiben:
\[\overline{PX} = \vert \overrightarrow X - \overrightarrow P \vert \quad \Longrightarrow \quad \overline{PX}(\lambda) = \vert \overrightarrow A + \lambda \cdot \overrightarrow u - \overrightarrow P \vert\]
2. Parameterwert \(\lambda_{min}\) für minimale Länge bestimmen:
\[\left. \begin{align*} &\overline{PX}^{\;\prime}(\lambda_{min}) \enspace = \enspace 0 \\ \\ &\overline{PX}^{\;\prime \prime}(\lambda_{min}) \; > \enspace 0 \end{align*} \right\} \quad \Longrightarrow \quad \lambda_{min} \]
3. Minimale Länge berechnen:
\[\overline{PX}(\lambda_{min}) = d\,(P;g)\]
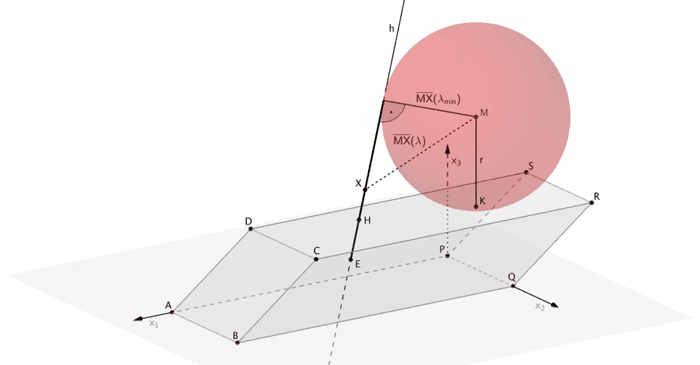
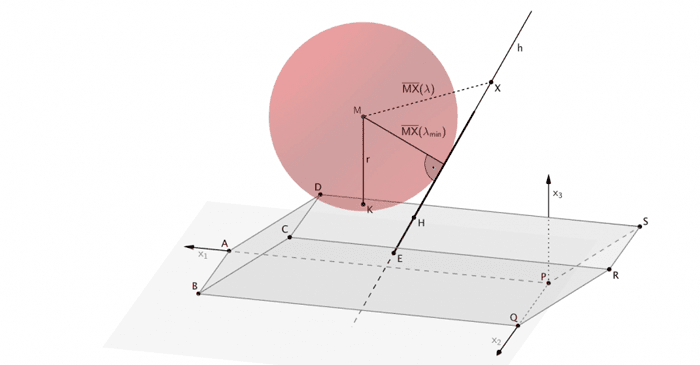
Länge der Strecke \([MX]\) zwischen dem Mittelpunkt \(M\) der Stahlkugel und einem beliebigen Punkt \(X ∈ h\) in Abhängigkeit des Parameters \(λ\) der Geradengleichung von \(h\)
\[X \in h\]
\[\overline{MX}'(\lambda) \overset{!}{=} 0 \quad \Longrightarrow \quad \lambda_{\text{min}}\]
\[d\,(M;h) = \overline{MX}(\lambda_{\text{min}})\]
C) Fallunterscheidung:
\(d\,(M;h) = 8 \quad \Longrightarrow \quad\) Die Stahlkugel berührt die Stange.
\(d\,(M;h) > 8 \quad \Longrightarrow \quad\) Die Stahlkugel berührt die Stange nicht.