Die Zufallsgröße \(Z\), die für eine Laplace-Münze die Anzahl des Auftretens von „Zahl" bei viermaligem Werfen beschreibt, hat ebenfalls den Erwartungswert 2 und es gilt analog \(P(Z = 2) = \frac{3}{8}\). Berechnen Sie die Varianz von \(Z\), vergleichen Sie diese mit der Varianz von \(Y\) und beschreiben Sie davon ausgehend einen qualitativen Unterschied der Wahrscheinlichkeitsverteilung von \(Z\) und \(Y\).
(2 BE)
Lösung zu Teilaufgabe 3c
Berechnung der Varianz der Zufallsgröße \(Z\)
Das viermalige Werfen einer Laplace-Münze stellt eine Bernoulli-Kette der Länge \(n = 4\) mit der Trefferwahrscheinlichkeit \(p = 0{,}5\) dar (hier für das Ereignis „Zahl").
Varianz \(Var(X)\) einer binomialverteilten Zufallsgröße \(X\):
\(Var(X) = n \cdot p \cdot (1 - p)\) (vgl. Merkhilfe)
Wobei \(n\) die Länge der Bernoulli-Kette und \(p\) die Trefferwahrscheinlichkeit für das Eintreten des betrachteten Ereignisses ist.
\[\begin{align*}Var(Z) &= n \cdot p \cdot (1 -p) \\[0.8em] &= 4 \cdot 0{,}5 \cdot (1 - 0{,}5) \\[0.8em] &= 1\end{align*}\]
Qualitativer Vergleich der Varianz von \(Z\) mit der Varianz von \(Y\)
\(Var(Z) = 1; \enspace Var(Y) = \dfrac{11}{8}\) (vgl. Teilaufgabe 3b)
\[\Longrightarrow \quad Var(Z) < Var(Y)\]
Die Varianz einer Zufallsgröße ist ein Maß für die Streuung der Werte einer Zufallsgröße um ihren Erwartungswert.
Der Vergleich zeigt, dass die Zufallsgröße \(Z\) eine geringere Streuung um den Erwartungswert hat als die Zufallsgröße \(Y\) (bei gleichem Erwartungswert \(E(Z) = E(Y) = 2\)).
Quantitativer Vergleich (nicht verlangt)
Die Zufallsgrößen \(Y\) und \(Z\) stimmen in ihren Werten, im Erwartungswert \(\textcolor{#cc071e}{\mu = 2}\) und in der Wahrscheinlichkeit \(\textcolor{#e9b509}{P(2)}\) überein.
| \(k\) | \(0\) | \(1\) | \(\textcolor{#cc071e}{2}\) | \(3\) | \(4\) |
| \(P(Y = k)\) | \(\textcolor{#0087c1}{\frac{1}{8}}\) | \(\textcolor{#89ba17}{\frac{3}{16}}\) | \(\textcolor{#e9b509}{\frac{3}{8}}\) | \(\textcolor{#89ba17}{\frac{3}{16}}\) | \(\textcolor{#0087c1}{\frac{1}{8}}\) |
| \(k\) | \(0\) | \(1\) | \(\textcolor{#cc071e}{2}\) | \(3\) | \(4\) |
| \(P(Z = k)\) | \(\textcolor{#0087c1}{P(Z = 0)}\) | \(\textcolor{#89ba17}{P(Z = 1)}\) | \(\textcolor{#e9b509}{\frac{3}{8}}\) | \(\textcolor{#89ba17}{P(Z = 3)}\) | \(\textcolor{#0087c1}{P(Z = 4)}\) |
Mit \(Var(Z) < Var(Y)\) - einer geringeren Streuung der Zufallsgröße \(Z\) - ist zu erwarten, dass sich die Wahrscheinlichkeitsverteilung der Zufallsgröße \(Z\) mehr um den Erwartungswert \(\textcolor{#cc071e}{\mu = 2}\) konzentriert als dies bei der Wahrscheinlichkeitsverteilung der Zufallsgröße \(Y\) der Fall ist.
Demnach müsste gelten:
\(\textcolor{#89ba17}{P(Z = 1) = P(Z = 3) > \dfrac{3}{16}}\) und wegen \(\sum P(Z = k) = 1\)
\(\textcolor{#0087c1}{P(Z = 0) = P(Z = 4) < \dfrac{1}{8}}\)
Mithilfe des Stochastischen Tafelwerks (ST) ergibt sich:
\[\textcolor{#89ba17}{P_{0{,}5}^{4}(Z = 1) = P_{0{}5}^{4}(Z = 3)} \overset{\text{ST}}{=} 0{,}25000 = \textcolor{#89ba17}{\frac{1}{4} > \frac{3}{16}}\]
\[\textcolor{#0087c1}{P_{0{,}5}^{4}(Z = 0) = P_{0{}5}^{4}(Z = 4)} \overset{\text{ST}}{=} 0{,}06250 = \textcolor{#0087c1}{\frac{1}{16} < \frac{1}{8}}\]
| \(k\) | \(0\) | \(1\) | \(\textcolor{#cc071e}{2}\) | \(3\) | \(4\) |
| \(P(Y = k)\) | \(\textcolor{#0087c1}{\frac{1}{8}}\) | \(\textcolor{#89ba17}{\frac{3}{16}}\) | \(\textcolor{#e9b509}{\frac{3}{8}}\) | \(\textcolor{#89ba17}{\frac{3}{16}}\) | \(\textcolor{#0087c1}{\frac{1}{8}}\) |
| \(k\) | \(0\) | \(1\) | \(\textcolor{#cc071e}{2}\) | \(3\) | \(4\) |
| \(P(Z = k)\) | \(\textcolor{#0087c1}{\frac{1}{16}}\) | \(\textcolor{#89ba17}{\frac{1}{4}}\) | \(\textcolor{#e9b509}{\frac{3}{8}}\) | \(\textcolor{#89ba17}{\frac{1}{4}}\) | \(\textcolor{#0087c1}{\frac{1}{16}}\) |
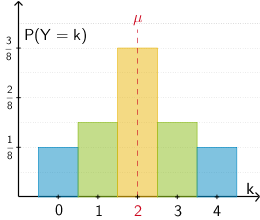
\(Var(Y) = \frac{11}{8}\) (größere Streuung)
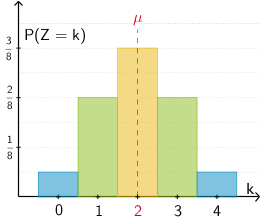
\(Var(Z) = 1\) (geringere Streuung)


