Geben Sie von folgenden Funktionen jeweils die maximale Definitionsmenge an. Bestimmen Sie jeweils die erste Ableitung der Funktion und vereinfachen Sie den Term der Ableitungsfunktion soweit wie möglich.

 

a) \(f(x) = -2\cos{(3- x)}\)

b) \(g(x) = \ln{\left( 2 - x^{2} \right)}\)

c) \(h(x) = \dfrac{-2 + e^{x}}{e^{x} - 1}\)

Anmerkung:

Die maximale Definitionsmenge der Funktionen \(f\), \(g\) und \(h\) ist jeweils lediglich anzugeben. Jede diesbezügliche Erklärung oder Rechnung kann entfallen.

 

a) Maximale Definitionsmenge und erste Ableitung der Funktion \(f\)

 

\[f(x) = -2\cos{(3- x)}\]

 

Maximale Definitionsmenge von \(f\)

 

\[\begin{align*} f(x) &= -2\cos{(3 - x)} \\[0.8em] &= -2\cos{[-(x - 3)]} & &| \; \cos{(-x)} = \cos{x} \\[0.8em] &= -2\cos{(x - 3)} \end{align*}\]

 

Die Kosinusfunktion \(x \mapsto \cos x\) ist in \(\mathbb R\) definiert.

Der Graph der Funktion \(f\) geht aus dem Graphen der Kosinusfunktion \(x \mapsto \cos{x}\) durch Spiegelung an der \(x\)-Achse, Streckung in \(y\)-Richtung um den Faktor \(2\) und Verschiebung um drei Einheiten in Richtung der positiven \(x\)-Achse hervor.

Durch die Entwicklung der Funktion \(f\) aus der Kosinusfunktion \(x \mapsto \cos{x}\) ändert sich die Definitionsmenge nicht.

 

\[\Longrightarrow \quad D_{f} = \mathbb R\]

 

Erste Ableitung \(f'\) von \(f\)

Die Funktion \(f\) wird mithilfe der Ableitung der Kosnusfunktion, der Kettenregel, der Ableitung einer Potenzfunktion sowie der Summen- und der Faktorregel abgeleitet.

 

\[f(x) = -2\cos{(3- x)}; \; D_{f} = \mathbb R\]

\[\left[u(v(x))\right]' = u'(v(x)) \cdot v'(x)\]

 

\[u(x) = \cos{x}; \; u'(x) = -\sin{x}\]

\[v(x) = 3 - x; \; v'(x) = 0 - 1 = -1\]

 

\[\begin{align*}f'(x) &= -2 \cdot \left[ -\sin{(3 - x)} \cdot (-1) \right] \\[0.8em] &= -2\sin{(3 - x)} & &| \; -\sin{x} = \sin{(-x)} \\[0.8em] &= 2\sin\left[ -(3 - x) \right] \\[0.8em] &= 2\sin{(x - 3)} \end{align*}\] 

 

b) Maximale Definitionsmenge und erste Ableitung der Funktion \(g\)

 

\[g(x) = \ln{\left( 2 - x^{2} \right)}\]

 

Maximale Definitionsmenge von \(g\)

Die natürliche Logarithmusfunktion \(x \mapsto \ln{x}\) ist in \(\mathbb R^{+}\) definiert.

 

\[\begin{align*}\Longrightarrow \quad 2 - x^{2} &> 0 & &| + x^{2} \\[0.8em] 2 &> x^{2} & &| \; \sqrt{\quad} \enspace \Big( \text{Es gilt:} \; \sqrt{a^{2}} = \vert a \vert; \; a \in \mathbb R \Big) \\[0.8em] \sqrt{2} &> \vert x \vert \end{align*}\]

 

\[\vert x \vert = \begin{cases} \begin{align*}x \; \text{für} \; x &> 0 \\[0.8em] -x \; \text{für} \; x &< 0 \end{align*} \end{cases}\]

 

Fallunterscheidung:

Die Betragsungleichung wird durch Fallunterscheidung gelöst. Für \(x > 0\) können die Betragsstriche entfallen. Für \(x < 0\) beschreibt \(-x\) die Funktionsweise des Betrags.

 

 

\[\Longrightarrow \quad -\sqrt{2} < x < \sqrt{2}\]

\[\Longrightarrow \quad D_{g} = \; ]-\sqrt{2};\sqrt{2}[\]

 

Alternative: Halbgeometrische Lösung der quadratischen Ungleichung \(2 - x^{2} > 0\)

 

\[\begin{align*}2 - x^{2} > 0 \\[0.8em] -x^{2} + 2 > 0 \end{align*}\]

 

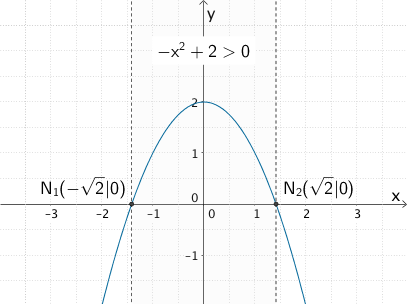
Die nach unten geöffnete Normalparabel mit der Gleichung \(y = -x^{2} + 2\) schneidet die \(x\)-Achse in den Punkten \(N_{1}(-\sqrt{2}|0)\) und \(N_{2}(\sqrt{2}|0)\). Für \(x \in \; ]-\sqrt{2};\sqrt{2}[\) verläuft die Parabel oberhalb der \(x\)-Achse.

 

\[\Longrightarrow \quad D_{g} = \; ]-\sqrt{2};\sqrt{2}[\]

  

Erste Ableitung \(g'\) von \(g\)

Die Funktion \(g\) kann unter Anwendung der Ableitung der natürlichen Logarithmusfunktion, der Kettenregel, der Ableitung einer Potenzfunktion sowie der Summenregel abgeleitet werden.

 

\[g(x) = \ln{\left( 2 - x^{2} \right)}; \; D_{g} = \; ]-\sqrt{2};\sqrt{2}[\]

\[\left[u(v(x))\right]' = u'(v(x)) \cdot v'(x)\]

 

\[u(x) = \ln{x}; \; u'(x) = \frac{1}{x}\]

\[v(x) = 2 - x^{2}; \; v'(x) = 0 - 2x = -2x\]

 

\[\begin{align*} g'(x) &= \frac{1}{2 - x^{2}} \cdot (-2x) \\[0.8em] &= -\frac{2x}{2 - x^{2}} \\[0.8em] &= \frac{2x}{x^{2} - 2}\end{align*}\]

 

c) Maximale Definitionsmenge und erste Ableitung der Funktion \(h\)

 

\[h(x) = \dfrac{-2 + e^{x}}{e^{x} - 1}\]

 

Maximale Definitionsmenge von \(h\)

Der Nenner der Funktion \(h\) darf nicht gleich Null sein.

 

Nullstelle des Nenners von \(h\) berechnen:

 

\[\begin{align*} e^{x} -1 &= 0 & &| + 1 \\[0.8em] e^{x} &= 1 & &| \; a^{x} = b \enspace \Longleftrightarrow \enspace x = \log_{a}{b} \\[0.8em] x &= \ln{1} & &| \; \log_{a}{1} = 0 \\[0.8em] x &= 0 \end{align*}\]

 

oder

 

\[\begin{align*} e^{x} -1 &= 0 & &| + 1 \\[0.8em] e^{x} &= 1 & &| \; \ln \; \text{(Logarithmieren)} \\[0.8em] \ln\left( e^{x} \right) &= \ln{1} & &| \; \ln{e^{x}} = x \; \left( \text{allg.:}\; \log_{a}{a^{x}} = x \right); \; \log_{a}{1} = 0 \\[0.8em] x &= 0 \end{align*}\]

 

oder

 

\[\begin{align*} e^{x} -1 &= 0 & &| + 1 \\[0.8em] e^{x} &= 1 \\[0.8em] e^{x} &= e^{0} & &| \; \text{Exponentenvergleich} \\[0.8em] x &= 0 \end{align*}\]

 

\[\Longrightarrow \quad D_{h} = \mathbb R \backslash \{0\}\]

 

Erste Ableitung \(h'\) von \(h\)

Die Funktion \(h\) lässt sich mithilfe der Quotientenregel, der Ableitung der natürlichen Exponentialfunktion sowie der Summenregel ableiten.

 

\[h(x) = \dfrac{-2 + e^{x}}{e^{x} - 1}; \; D_{h} = \mathbb R \backslash \{0\}\]

\[\left[ \frac{u(x)}{v(x)} \right]' = \frac{u'(x) \cdot v(x) - u(x) \cdot v'(x)}{\left[ v(x) \right]^{2}}\]

 

\[u(x) = -2 + e^{x}; \; u'(x) = 0 + e^{x} = e^{x}\]

\[v(x) = e^{x} - 1; \; v'(x) = e^{x} - 0 = e^{x}\]

 

\[\begin{align*} h'(x) &= \frac{e^{x} \cdot \left( e^{x} - 1 \right) - \left( -2 + e^{x} \right) \cdot e^{x}}{\left( e^{x} - 1 \right)^{2}} \\[0.8em] &= \frac{e^{x} \cdot \left( e^{x} - 1 + 2 - e^{x} \right)}{\left( e^{x} - 1 \right)^{2}} \\[0.8em] &= \frac{e^{x}}{\left( e^{x} - 1 \right)^{2}} \end{align*}\]