Abiturlösungen Mathematik Bayern Beispiel-Abiturprüfung 2014 Prüfungsteil B Geometrie 2
- Details
- Kategorie: Geometrie 2
Die Abbildung zeigt einen Würfel der Kantenlänge 6. Die Koordinaten der Eckpunkte \(A\,(0|0|0)\), \(D\,(0|6|0)\) und \(G\,(6|6|6)\) sind gegeben.
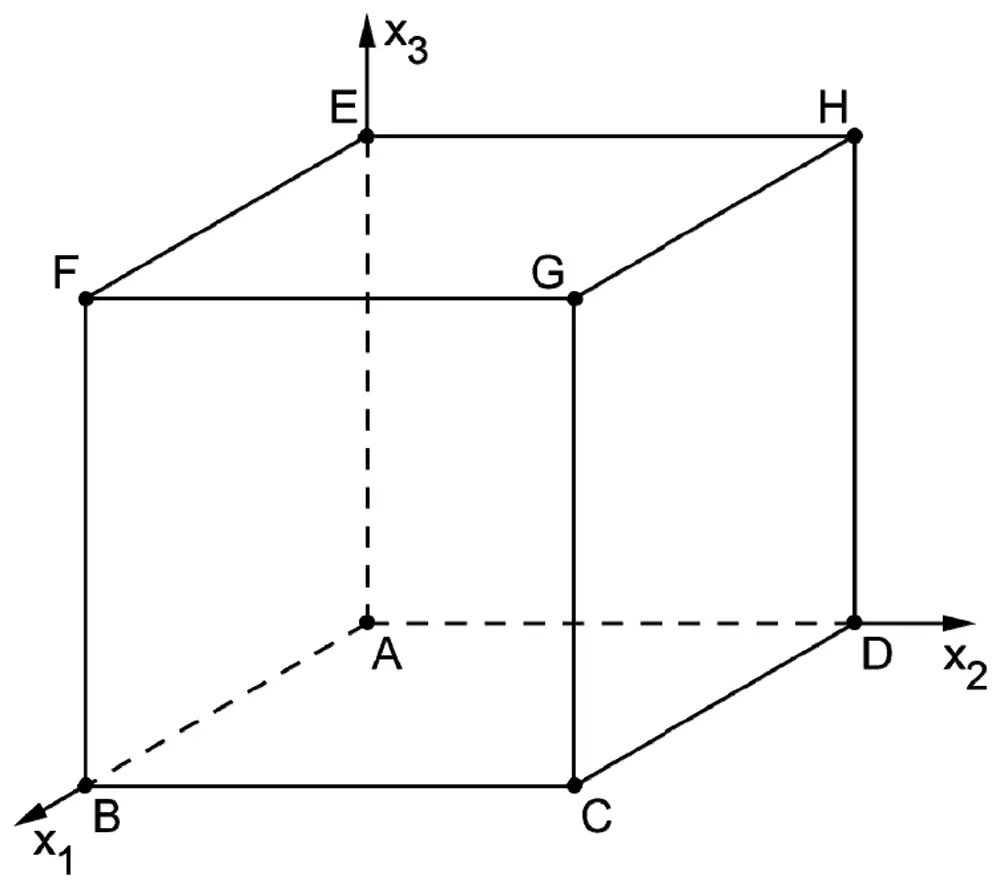
Die Punkte \(B\), \(E\) und \(G\) liegen in einer Ebene \(L\). Bestimmen Sie eine Gleichung von \(L\) in Normalenform. Zeichnen Sie die Figur, in der die Ebene \(L\) den Würfel schneidet, in die Abbildung ein.
(mögliches Ergebnis: \(L\,\colon\; x_1 - x_2 + x_3 = 6\))
(5 BE)
- Details
- Kategorie: Geometrie 2
Der Würfel wird entlang der Ebene \(L\) geteilt. Berechnen Sie das Volumen der entstehenden Pyramide. Geben Sie an, wie viel Prozent des Würfelvolumens die Pyramide einnimmt.
(4 BE)
- Details
- Kategorie: Geometrie 2
Die Ebene \(M\,\colon\; x_1 - x_2 + x_3 = 3\) schneidet den Würfel in einem regulären Sechseck.
Begründen Sie, dass \(M\) parallel zu \(L\) ist. Geben Sie die Schnittpunkte von \(M\) mit der \(x_1\)-Achse sowie mit der \(x_3\)-Achse an und weisen Sie nach, dass \(M\) den Mittelpunkt der Strecke \([BC]\) enthält.
(4 BE)
- Details
- Kategorie: Geometrie 2
Zeichnen Sie die sechs Punkte, in denen \(M\) die Kanten des Würfels schneidet, sowie die sechseckige Schnittfigur in die Abbildung ein.
(3 BE)
- Details
- Kategorie: Geometrie 2
Jede Ebene, die parallel zu \(M\) verläuft, wird durch eine Gleichung der Form \(x_1 - x_2 + x_3 = p\) mit \(p \in \mathbb R\) beschrieben. Nennen Sie die Arten der Figuren, in denen eine solche Ebene den Würfel schneiden kann, und geben Sie die Menge aller Werte von \(p\) an, für die die Schnittfigur ein Sechseck ist.
(4 BE)


