Gegeben ist die Schar der in \(\mathbb R\) definierten Funktionen \(f_{a} \colon x \mapsto xe^{ax}\) mit \(a \in \mathbb R \, \backslash \,\{0\}\). Ermitteln Sie, für welchen Wert von \(a\) die erste Ableitung von \(f_{a}\) an der Stelle \(x = 2\) den Wert 0 besitzt.
(4 BE)
Lösung zu Teilaufgabe 4
Waagrechte Tangente einer Funktionenschar
\[f_{a}(x) = xe^{ax}\,; \enspace D = \mathbb R\,, \enspace a \in \mathbb R \, \backslash \, \{0\}\]
Bedingung: \(f'_{a}(2) = 0\)
Graphisch interpretiert, bedeutet die Bedingung, dass der Graph einer Scharfunktion der Funktionenschar \(f_{a}\) an der Stelle \(x = 2\) eine waagrechte Tangente besitzen soll. Gesucht ist der Wert des Parameters \(a\) der zugehörigen Scharfunktion.
Anwendung der Differetialrechnung:
Steigung \(m_{T}\) einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\,(\,x_0\,|\,f(x_0)\,)\)
\[m_{T} = f'(x_0)\]
(vgl. Merkhilfe)
Erste Ableitung \(f'_{a}\) von \(f_{a}\) bilden:
Ableitung einer Potenzfunktion
\[ f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
Ableitung der natürlichen Exponentialfunktion
\[ f(x) = e^x \quad \Longrightarrow \quad f'(x) = e^x\]
Produktregel
\[f(x) = u(x) \cdot v(x) \quad \Longrightarrow \quad f'(x) = u'(x) \cdot v(x) + u(x) \cdot v'(x)\]
Kettenregel
\[ f(x) = u(v(x)) \quad \Longrightarrow \quad f'(x) = u'(v(x)) \cdot v'(x) \]
(vgl. Merkhilfe)
\[\begin{align*} f_{a}(x) = xe^{ax} \quad \Longrightarrow \quad f'_{a}(x) &= 1 \cdot e^{ax} + x \cdot e^{ax} \cdot a \\[0.8em] &= e^{ax} \cdot (1 + ax) \end{align*}\]
\[\begin{align*} f'_{a}(2) \overset{!}{=} 0 \quad \Longrightarrow \quad \underset{>\,0}{e^{2a}} \cdot (1 + 2a) &= 0 \\[0.8em] \Longrightarrow \quad 1 + 2a &= 0 & &| - 1 \\[0.8em] 2a &= -1 & &| : 2 \\[0.8em] a &= -0{,}5 \end{align*}\]
Für \(a = -0{,}5\) besitzt die erste Ableitung \(f'_{-0{,}5}\) der Scharfunktion \(\displaystyle f_{-0{,}5} \colon x \mapsto xe^{-0{,}5x}\) an der Stelle \(x = 2\) den Wert 0.
bzw.
Für \(a = -0{,}5\) besitzt der Graph \(G_{f_{-0{,}5}}\) der Scharfunktion \(\displaystyle f_{-0{,}5} \colon x \mapsto xe^{-0{,}5x}\) an der Stelle \(x = 2\) eine waagrechte Tangente.
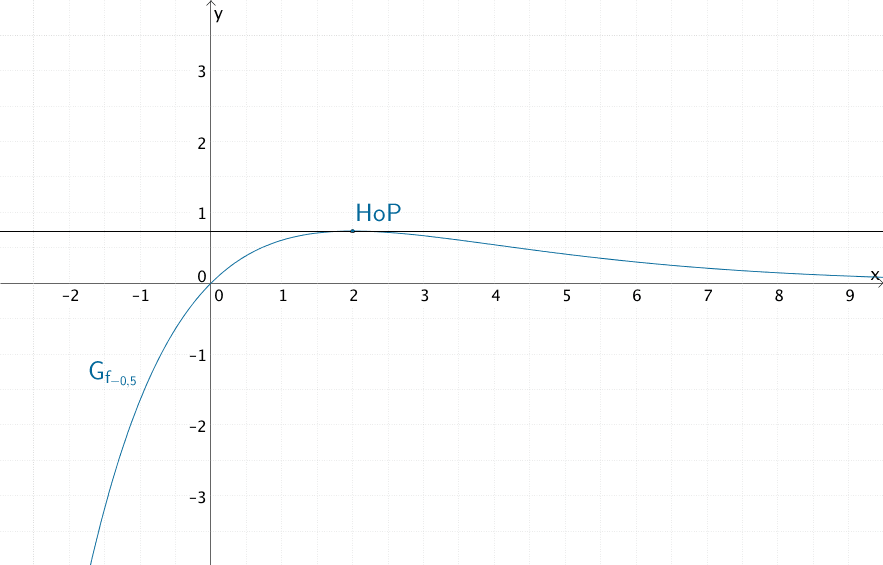
Der Graph \(G_{f_{-0{,}5}}\) der Scharfunktion \(\displaystyle f_{-0{,}5} \colon x \mapsto xe^{-0{,}5x}\) besitzt an der Stelle \(x = 2\) einen Hochpunkt und damit eine waagrechte Tangente.

