Es gibt einen Wert von \(c\), für den der Flächeninhalt \(A(c)\) des Rechtecks \(PQRS\) maximal ist. Berechnen Sie diesen Wert von \(c\).
(4 BE)
Lösung zu Teilaufgabe 1f
\(A(c) = 4c \cdot e^{-\frac{1}{8}c^2}; \; c \in \mathbb R^{+}\) (vgl. Teilaufgabe 1e)
Notwendige Bedingung für einen maximalen Flächeninhalt \(\boldsymbol{A(c)}\)
Anwendung der Differentialrechnung:
Extrempunkte
Ist \(f'(x_{0}) = 0\) und wechselt \(f'\) an der Stelle \(x_{0}\) das Vorzeichen, so hat \(G_{f}\) an der Stelle \(x_{0}\) einen Extrempunkt.
(vgl. Merkhilfe)
\[A'(c) = 0\]
Erste Ableitungsfunktion \(A'\) bilden:
Hierfür wird die Produktregel, die Kettenregel und die Faktorregel sowie die Ableitung der natürlichen Exponentialfunktion und die Ableitung einer Potenzfunktion benötigt.
\[A(c) = \textcolor{#0087c1}{4c} \cdot \textcolor{#cc071e}{e^{-\frac{1}{8}c^2}}\]

Ableitungen der Grundfunktionen
\[c' = 0 \enspace (c \in \mathbb R)\]
\[\left( x^r \right)' = r \cdot x^{r - 1} \enspace (r \in \mathbb R)\]
\[\left( \sqrt{x} \right)' = \frac{1}{2\sqrt{x}}\]
\[\left( \sin{x} \right)' = \cos{x}\]
\[\left( \cos{x} \right)' = -\sin{x}\]
\[\left( \ln{x} \right)' = \frac{1}{x}\]
\[\left( \log_{a}{x}\right)' = \frac{1}{x \cdot \ln{a}}\]
\[\left( e^x \right)' = e^x\]
\[\left(a^x \right)' = a^x \cdot \ln{a}\]
Faktorregel
\[\begin{align*}f(x) &= a \cdot \textcolor{#0087c1}{u(x)} \\[0.8em] f'(x) &= a \cdot \textcolor{#0087c1}{u'(x)}\end{align*}\]
Summenregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(x)} + \textcolor{#cc071e}{v(x)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(x)} + \textcolor{#cc071e}{v'(x)}\end{align*}\]
Produktregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v(x)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(x)} \cdot \textcolor{#cc071e}{v(x)} + \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v'(x)}\end{align*}\]
Quotientenregel
\[\begin{align*}f(x) &= \dfrac{\textcolor{#0087c1}{u(x)}}{\textcolor{#cc071e}{v(x)}} \\[0.8em] f'(x) &= \dfrac{\textcolor{#0087c1}{u'(x)} \cdot \textcolor{#cc071e}{v(x)} - \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v'(x)}}{[\textcolor{#cc071e}{v(x)}]^{2}}\end{align*}\]
Kettenregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(}\textcolor{#cc071e}{v(x)}\textcolor{#0087c1}{)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(}\textcolor{#cc071e}{v(x)}\textcolor{#0087c1}{)} \cdot \textcolor{#cc071e}{v'(x)}\end{align*}\]
\[\begin{align*} A'(c) &= \underbrace{\textcolor{#0087c1}{4} \cdot \textcolor{#cc071e}{e^{-\frac{1}{8}c^2}} + \textcolor{#0087c1}{4c} \cdot \overbrace{\textcolor{#cc071e}{e^{-\frac{1}{8}c^2} \cdot \left( -\frac{1}{8} \cdot 2c \right)}}^{\large{\text{Kettenregel}}}}_{\large{\text{Produktregel}}} \\[0.8em] &= 4 \cdot e^{-\frac{1}{8}c^2} - c^2 \cdot e^{-\frac{1}{8}c^2} &&| \; e^{-\frac{1}{8}c^2}\;\text{ausklammern} \\[0.8em] &= (4 - c^2) \cdot e^{-\frac{1}{8}c^2} \end{align*}\]
Nullstelle von \(A'(c)\) berechnen:
\[A'(c) = (4 - c^2) \cdot \underbrace{e^{-\frac{1}{8}c^2}}_{>\,0}\]
\[\begin{align*}A'(c) = 0 \; \Rightarrow \; 4 - c^2 &= 0 &&| + c^2 \\[0.8em] 4 &= c^2 &&| \; \sqrt{\quad}\enspace (c \in \mathbb R^+\;\text{vgl. Angabe}) \\[0.8em] 2 &= c \end{align*}\]
Nachweis, dass \(\boldsymbol{A(2)}\) maximaler Flächeninhalt des Rechtecks \(\boldsymbol{PQRS}\) ist
Anwendung der Differentialrechnung:
Extrempunkte
Ist \(f'(x_{0}) = 0\) und wechselt \(f'\) an der Stelle \(x_{0}\) das Vorzeichen, so hat \(G_{f}\) an der Stelle \(x_{0}\) einen Extrempunkt.
(vgl. Merkhilfe)
\[A'(c) = \textcolor{#e9b509}{(4 - c^2)} \cdot \underbrace{e^{-\frac{1}{8}c^2}}_{>\,0}\]
Der Faktor \(\textcolor{#e9b509}{(4 - c^2)}\) bestimmt den Vorzeichenwechsel von \(\boldsymbol{A'(c)}\) an der Stelle \(c = 2\).
Kurzform:
Mit \(A'(1) \textcolor{#0087c1}{> 0}\) und \(A'(3) \textcolor{#cc071e}{< 0}\) ist \(A(2)\) maximaler Flächeninhalt des Rechtecks \(PQRS\).
Monotonietabelle:
| \(c\) | \(]0;2[\) | \(2\) | \(]2;+\infty[\) |
| \(\textcolor{#e9b509}{(4 - c^2)}\) | \(\textcolor{#0087c1}{+}\) | \(\textcolor{#cc071e}{–}\) | |
| \(A'(c)\) | \(\textcolor{#0087c1}{+}\) | \(0\) | \(\textcolor{#cc071e}{–}\) |
| \(G_A\) | \(\textcolor{#0087c1}{\nearrow}\) | \(\text{Max.}\) | \(\textcolor{#cc071e}{\searrow}\) |
Geeignete Testwerte sind beispielsweise \(c = 1\) und \(c = 3\) bzw, \(A'(1)\) und \(A'(3)\).
Halbgraphischer Nachweis:
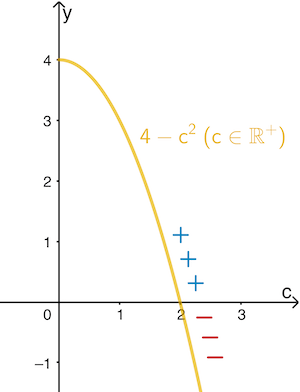
Der Graph des Faktors \(\textcolor{#e9b509}{(4 - c^2)}\) ist für \(c \in \mathbb R^+\) der rechte Ast einer nach unten geöffneten Parabel, die an der Nullstelle \(c = 2\) einen Vorzeichenwechsel von \(\textcolor{#0087c1}{\boldsymbol{+}}\) nach \(\textcolor{#cc071e}{\boldsymbol{\Large{–}}}\) hat.
Somit wechselt \(A'(c)\) an der Stelle \(c = 2\) das Vorzeichen von \(\textcolor{#0087c1}{\boldsymbol{+}}\) nach \(\textcolor{#cc071e}{\boldsymbol{\Large{–}}}\) und \(\boldsymbol{A(2)}\) ist maximaler Flächeninhalt des Rechtecks \(PQRS\).


