Aus den vier Austrittsstellen fließen pro Sekunde insgesamt 80 mi Wasser in die Bronzeschale. Bestimmen Sie die Zeit in Sekunden, die vergeht, bis der anfangs leere Brunnen vollständig mit Wasser gefüllt ist.
(4 BE)
Lösung zu Teilaufgabe h
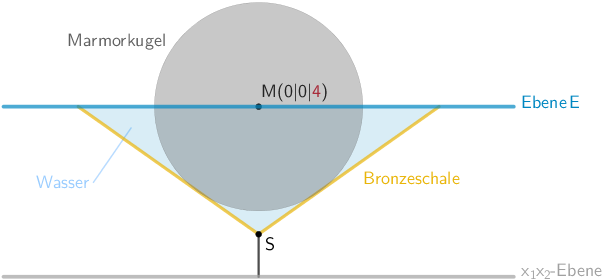
Planskizze (optional): Wenn der Brunnen vollständig gefüllt ist, reicht das Wasser bis zur Ebene \(\textcolor{#0087c1}{E}\), welche im Abstand 4 parallel zur \(x_{1}x_{2}\)-Ebene liegt (vgl. Teilaufgabe a).
Da der Mittelpunkt \(M(0|0|\textcolor{#cc071e}{4})\) der Marmorkugel ebenfalls in der Ebene \(\textcolor{#0087c1}{E}\) liegt und die Kugel die Bronzeschale berührt (vgl. Angabe), folgt:
Volumen einer Kugel (vgl. Merkhilfe)
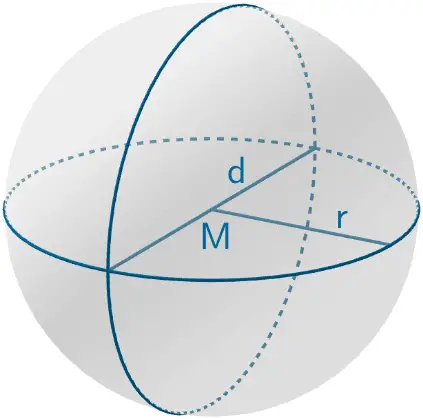
\[V_{\text{Kugel}} = \frac{4}{3} \cdot r^3 \cdot \pi\]
\[\begin{align*}V_{\textcolor{#99ccff}{\text{Wasser}}} &= V_{\textcolor{#e9b509}{\text{Pyramide}}} - V_{\textcolor{#606060}{\text{Halbkugel}}} &&| \; V_{\textcolor{#e9b509}{\text{Pyramide}}} = 72\;\text{(vgl. Teilaufgabe c)} \\[0.8em] &= 72 - \frac{1}{2} \cdot \frac{4}{3} \cdot r^{3} \cdot \pi &&| \; r = \sqrt{6}\;\text{(vgl. Teilaufgabe d)} \\[0.8em] &= 72 - \frac{2}{3} \cdot \left(\sqrt{6}\right)^{3} \cdot \pi \\[0.8em] &= 72 - \frac{2}{3} \cdot 6\sqrt{6} \cdot \pi \\[0.8em] &= 72 - 4\sqrt{6} \cdot \pi \end{align*}\]
Das Volumen des Wassers beträgt also \((72-4\sqrt{6}\cdot\pi)\) Kubikdezimeter bzw. \((72-4\sqrt{6}\cdot\pi)\) Liter (Eine Längeneinheit entspricht einem Dezimeter, vgl. Angabe).
Pro Sekunde fließen insgesamt 80 ml (Milliliter) = 0,08 l (Liter) in die Bronzeschale.
\[\frac{(72 - 4\sqrt{6}\cdot\pi)\,\text{l}}{0{,}08\,\frac{\text{l}}{\text{s}}} \approx 515\,\text{s}\]
Nach ca. 515 Sekunden ist der anfangs leere Brunnen vollständig mit Wasser gefüllt.


