Geben Sie die Koordinaten zweier Punkte \(P\) und \(Q\) an, die auf \(g\) liegen und von \(T\) gleich weit entfernt sind.
(2 BE)
Lösung zu Teilaufgabe 2b
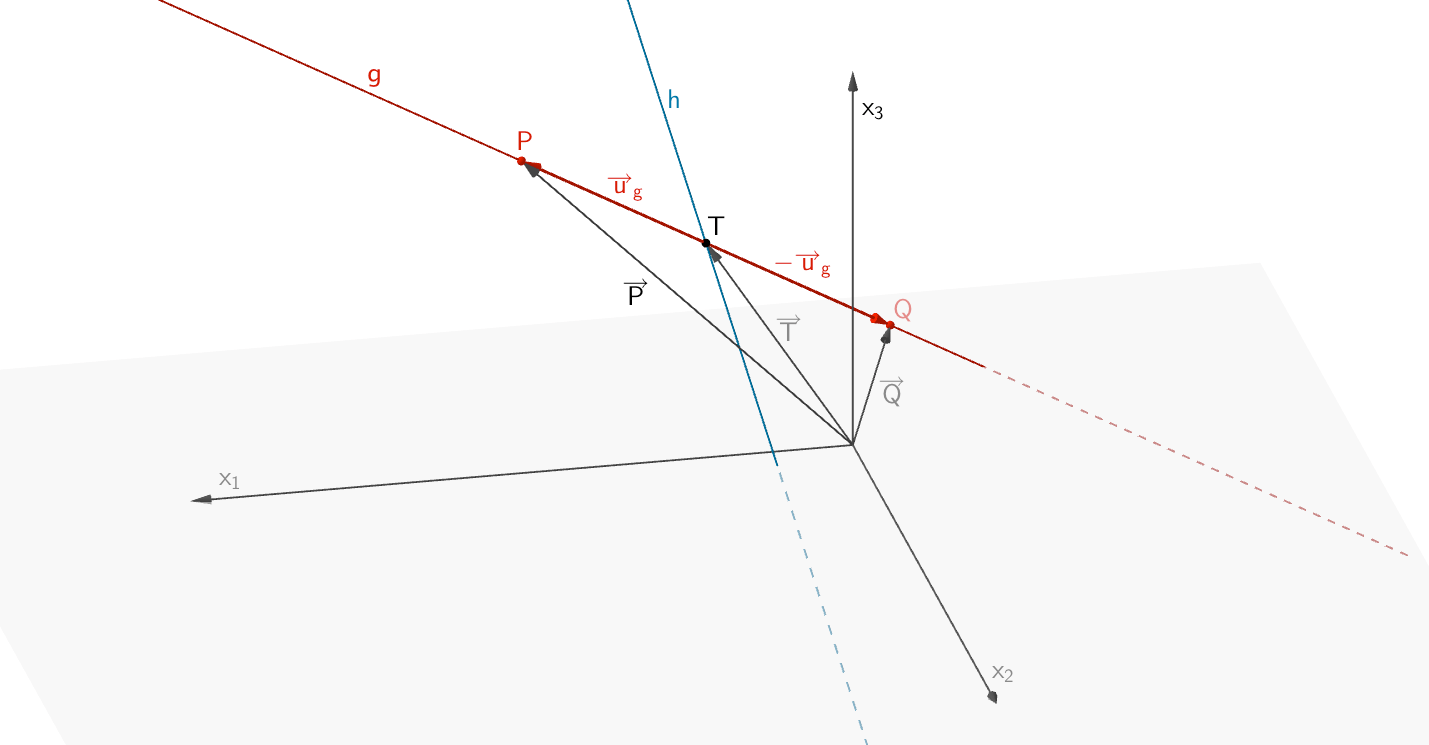
1. Lösungsansatz: Richtungsvektor von \(g\) und Gegenvektor
Die beiden Punkte \(P \in g\) und \(Q \in g\) sind vom Punkt \(T\) um die Länge des Richtungsvektors \(\overrightarrow{u}_g\) der Geraden \(g\) entfernt.
\[g\,\colon\; \overrightarrow{X} = \begin{pmatrix} 8 \\ 1 \\ 7 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix}\,; \quad \overrightarrow{u}_g = \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix}\]
\[T\,(2|-1|3)\]
\[\overrightarrow{P} = \overrightarrow{T} + \overrightarrow{u}_g = \begin{pmatrix} 2 \\ -1 \\ 3 \end{pmatrix} + \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} = \begin{pmatrix} 5 \\ 0 \\ 5 \end{pmatrix}\]
\[\Longrightarrow \quad P\,(5|0|5)\]
\[\overrightarrow{Q} = \overrightarrow{T} - \overrightarrow{u}_g = \begin{pmatrix} 2 \\ -1 \\ 3 \end{pmatrix} - \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} = \begin{pmatrix} -1 \\ -2 \\ 1 \end{pmatrix}\]
\[\Longrightarrow \quad Q\,(-1|-2|1)\]
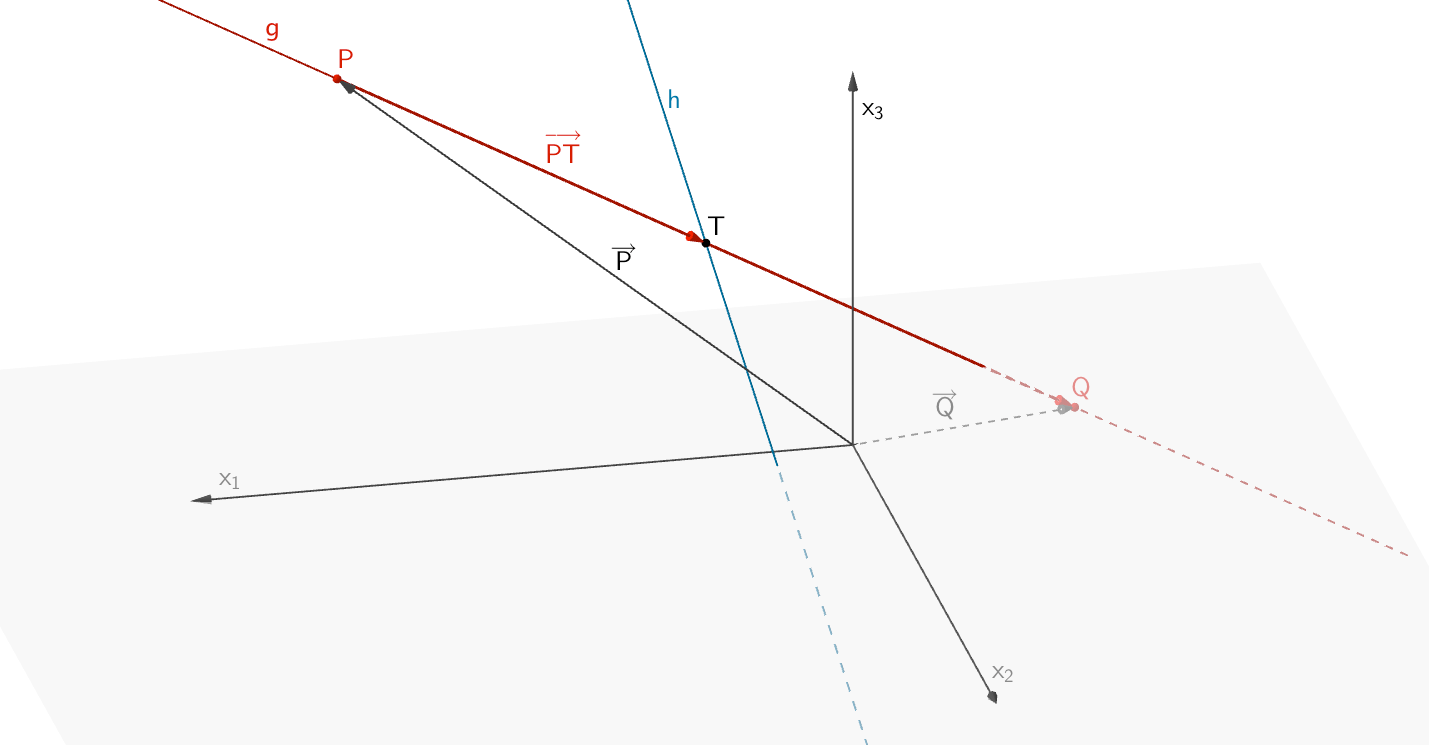
2. Lösungsansatz: Aufpunkt von \(g\) wählen
Es sei \(P\) der Aufpunkt von \(g\):
\[g\,\colon\; \overrightarrow{X} = \begin{pmatrix} 8 \\ 1 \\ 7 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix}\]
\[\Longrightarrow \quad P\,(8|1|7)\]
Koordinaten des Punktes \(Q\) bestimmen:
\[P\,(8|1|7)\,, \enspace T\,(2|-1|3)\]
\[\begin{align*}\overrightarrow{Q} &= \overrightarrow{P} + 2 \cdot \overrightarrow{PT} \\[0.8em] &= \overrightarrow{P} + 2 \cdot \left( \overrightarrow{T} - \overrightarrow{P}\right) \\[0.8em] &= \begin{pmatrix} 8 \\ 1 \\ 7 \end{pmatrix} + 2 \cdot \left[ \begin{pmatrix}2 \\ -1 \\ 3 \end{pmatrix} - \begin{pmatrix} 8 \\ 1 \\ 7 \end{pmatrix} \right] \\[0.8em] &= \begin{pmatrix} 8 \\ 1 \\ 7 \end{pmatrix} + 2 \cdot \begin{pmatrix} -6 \\ -2 \\ -4 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} -4 \\ -3 \\ -1 \end{pmatrix} \end{align*}\]
\[\Longrightarrow \quad Q\,(-4|-3|-1)\]
Aufpunkt \(P\) der Geraden \(g\); Der Punkt \(Q \in g\) liegt vom Schnittpunkt \(T\) der Geraden \(g\) und \(h\) um \(\overline{TQ} = \vert \overrightarrow{PT} \vert\) entfernt.