Der Bohrkanal wird geradlinig verlängert und verlässt die wasserführende Gesteinsschicht in einer Tiefe von 3600 m unter der Erdoberfläche. Die Austrittsstelle wird im Modell als Punkt \(R\) auf der Geraden \(PQ\) beschrieben. Bestimmen Sie die Koordinaten von \(R\) und ermitteln Sie die Dicke der wasserführenden Gesteinsschicht auf Meter gerundet.
(zur Kontrolle: \(x_{1}\)- und \(x_{2}\)-Koordinate von \(R\): \(1{,}04\))
(6 BE)
Lösung zu Teilaufgabe d
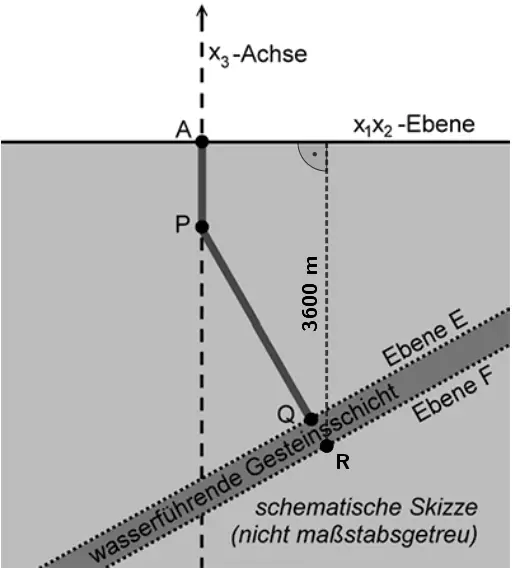
Da der Bohrkanal die wasserführende Gesteinsschicht in einer Tiefe von 3600 m verlässt, hat der Punkt \(R\) im Modell die Koordinaten \(R(r_{1}|r_{2}| -3{,}6)\).
Bestimmung der Koordinaten von \(R\)
Der Punkt \(R\) liegt auf der Geraden \(PQ\) (vgl. Angabe).
Mit \(P(0|0|-1)\) und \(\overrightarrow{PQ} = \begin{pmatrix} 1 \\ 1 \\ -2{,}5 \end{pmatrix}\) (vgl. Teilaufgabe a) ist eine Gleichung der Geraden \(PQ\) beispielsweise gegebnen durch:
Gleichung einer Gerade / Strecke in Parameterform
Jede Gerade \(g\) kann durch eine Gleichung in der sogenannten Parameterform
\(g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u} \enspace\) mit dem Parameter \(\lambda \in \mathbb R\) beschrieben werden.
Dabei ist \(\overrightarrow{A}\) der Ortsvektor eines Aufpunkts (Stützvektor) und \(\overrightarrow{u}\) ein Richtungsvektor der Gerade \(g\).
Gleichung einer Strecke \([AB]\) in Parameterform:
\[\overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{AB}, \; \textcolor{#cc071e}{\lambda \in [0;1]} \]
\[\begin{align*} PQ \colon \overrightarrow{X} &= \overrightarrow{P} + \lambda \cdot \overrightarrow{PQ}; \; \lambda \in \mathbb R \\[0.8em] PQ \colon \overrightarrow{X} &= \begin{pmatrix} 0 \\ 0 \\ -1 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 1 \\ 1 \\ -2{,}5 \end{pmatrix}; \; \lambda \in \mathbb R \end{align*}\]
Mit \(R(r_{1}|r_{2}|-3{,}6) \in PQ\) folgt:
\[R \in PQ \colon \begin{pmatrix} r_{1} \\ r_{2} \\ \textcolor{#0087c1}{-3{,}6} \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ \textcolor{#0087c1}{-1} \end{pmatrix} + \lambda \cdot \begin{pmatrix} 1 \\ 1 \\ \textcolor{#0087c1}{-2{,}5} \end{pmatrix}; \; \lambda \in \mathbb R\]
Die dritte Zeile der Vektorgleichung liefert den Wert des Parameters \(\lambda\) für die Berechnung der Koordinaten \(r_{1}\) und \(r_{2}\) des Punktes \(R\).
\[\begin{align*} -3{,}6 &= -1 - 2{,}5\lambda &&| + 2{,}5\lambda + 3{,}6 \\[0.8em] 2{,}5\lambda &= 2{,}6 &&| : 2{,}5 \\[0.8em] \lambda &= 1{,}04 \end{align*}\]
\(\lambda = 1{,}04\) in die Gleichung der Geraden \(PQ\) eingesetzt:
\[R \in PQ \colon \overrightarrow{R} = \begin{pmatrix} 0 \\ 0 \\ -1 \end{pmatrix} + 1{,}04 \cdot \begin{pmatrix} 1 \\ 1 \\ -2{,}5 \end{pmatrix} = \begin{pmatrix} 1{,}04 \\ 1{,}04 \\ -3{,}6 \end{pmatrix}\]
\[\Longrightarrow \quad R(1{,}04|1{,}04|-3{,}6)\]
Dicke der wasserführenden Gesteinsschicht auf Meter gerundet
Im Modell wird die Dicke der wasserführenden Gesteinsschicht durch die Länge der Strecke \([QR]\) beschrieben.
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\(Q(1|1|-3{,}5)\), \(R(1{,}04|1{,}04|-3{,}6)\)
\[\begin{align*}\overline{QR} &= \vert \overrightarrow{QR} \vert = \vert \overrightarrow{R} - \overrightarrow{Q} \vert \\[0.8em] &= \left| \begin{pmatrix} 1{,}04 \\ 1{,}04 \\ -3{,}6 \end{pmatrix} - \begin{pmatrix} 1 \\ 1 \\ -3{,}5 \end{pmatrix} \right| = \left| \begin{pmatrix} 0{,}04 \\ 0{,}04 \\ -0{,}1 \end{pmatrix} \right| \\[0.8em] &= \sqrt{0{,}04^{2} + 0{,}04^{2} + (-0{,}1)^{2}} = \frac{\sqrt{33}}{50} \\[0.8em] &\approx 0{,}115 \end{align*}\]
Eine Längeneinheit entspricht einem Kilometer (vgl. Angabe).
\[0{,}115 \cdot 1000\, \text{m} = 115\, \text{m}\]
Die Dicke der wasserführende Gesteinsschicht beträgt etwa 115 Meter.


