Durch die Rotation des Vierecks \(MTSF\) um die Gerade \(MS\) entsteht ein Körper. Beschreiben Sie diesen Körper.
In einer Formelsammlung ist zur Berechnung des Volumens eines solchen Körpers die Formel \(V = \frac{1}{3} \cdot \left( \frac{a}{2} \right)^{2} \cdot \pi \cdot b\) zu finden. Geben Sie für den beschriebenen Körper die Strecken an, deren Längen für \(a\) bzw. \(b\) einzusetzen sind.
(4 BE)
Lösung zu Teilaufgabe f
Beschreibung des Rotationskörpers
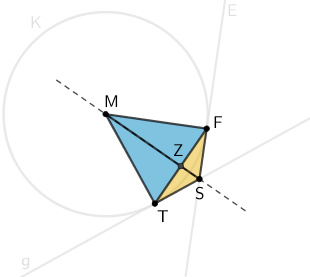
Durch Rotation des Vierecks \(MTSF\) um die Gerade \(MS\) entsteht ein Doppelkegel.
Beide Kegel (gerade Kreiskegel) haben denselben Grundkreis mit dem Durchmesser \([TF]\) und dem Mittelpunkt \(Z\).
Der größere Kegel hat seine Spitze im Punkt \(M\) und somit die Höhe \([ZM]\). Der kleinere Kegel hat seine Spitze im Punkt \(S\) und somit die Höhe \(ZS\)
Zuordnung von \(a\) und \(b\) der Formel \(V = \frac{1}{3} \cdot \left( \frac{a}{2} \right)^{2} \cdot \pi \cdot b\)
In der Formel steht \(a\) für die Länge der Strecke \([TF]\) und \(b\) für die Länge der Strecke \([MS]\).
Ausführliche Erklärung (nicht verlangt)
Für das Volumen eines geraden Kreiskegels gilt: \(V_{\text{Kegel}} = \frac{1}{3} \cdot r^{2} \cdot \pi \cdot h\). Dabei ist \(r\) der Radius des Grundkreises und \(h\) die Höhe des Kegels. Das Volumen des Doppelkegel lässt sich damit wie folgt bestimmen:
Volumen eines geraden Kreiskegels
\[V = \frac{1}{3}r^{2} \pi h\]
(vgl. Merkhilfe)
\[\begin{align*} V_{\text{Doppelkegel}} &= V_{\textcolor{#0087c1}{\text{Kegel groß}}} + V_{\textcolor{#e9b509}{\text{Kegel klein}}} \\[0.8em] &= \frac{1}{3} \cdot \left( \frac{\overline{TF}}{2} \right)^{2} \cdot \pi \cdot \overline{ZM} + \frac{1}{3} \cdot \left( \frac{\overline{TF}}{2} \right)^{2} \cdot \pi \cdot \overline{ZS} \\[0.8em] &= \frac{1}{3} \cdot \left( \frac{\overline{TF}}{2} \right) \cdot \pi \left( \overline{ZM} + \overline{ZS} \right) &&|\; \overline{ZM} + \overline{ZS} = \overline{MS} \\[0.8em] &= \frac{1}{3} \cdot \left( \frac{\textcolor{#89ba17}{\overline{TF}}}{2} \right) \cdot \pi \cdot \textcolor{#89ba17}{\overline{MS}}\end{align*}\]
In der Formel \(V = \dfrac{1}{3} \cdot \left( \dfrac{\textcolor{#89ba17}{a}}{2} \right)^{2} \cdot \pi \cdot \textcolor{#89ba17}{b}\) steht also \(a\) für die Länge der Strecke \([TF]\) und \(b\) für die Länge der Strecke \([MS]\).


