Die Abbildung zeigt den Graphen \(G_{f}\) einer in \(\mathbb R\) definierten Funktion \(f\) mit dem Wendepunkt \(W(1|4)\).
Ermitteln Sie mithilfe der Abbildung näherungsweise den Wert der Ableitung von \(f\) an der Stelle \(x = 1\).
Skizzieren Sie den Graphen der Ableitungsfunktion \(f'\) von \(f\) in die Abbildung; berücksichtigen Sie dabei insbesondere die Lage der Nullstellen von \(f'\) sowie den für \(f'(1)\) ermittelten Näherungswert.
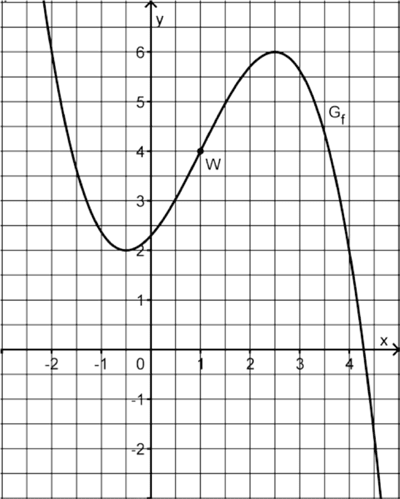
(3 BE)
Lösung zu Teilaufgabe 4
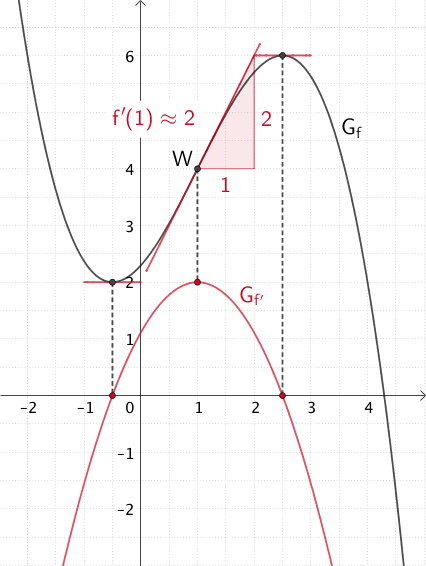
Erläuterung (nicht verlangt):
Die erste Ableitung \(f'\) beschreibt die Steigung einer Tangente an den Graphen der Funktion \(f\). Die Steigung der Tangente an \(G_{f}\) an der Stelle \(x = 1\) ist also gleich dem Funktionswert \(f'(1)\). Um einen Näherungswert von \(f'(1)\) mithilfe der Abbildung zu ermitteln, wird zunächst die Wendetangente im Wendepunkt \(W\) eingezeichnet. Anschließend lässt sich anhand eines Steigungsdreiecks die Steigung der Tangente ermitteln.
An den Extremstellen hat der Graph der Funktion \(f\) jeweils eine waagrechte Tangente, d.h. die Tangentensteigung ist gleich Null. Deshalb entsprechen die Extremstellen von \(G_{f}\) den Nullstellen des Graphen von \(f'\).


