Aus der Bevölkerung Deutschlands wird eine Person zufällig ausgewählt und getestet. Beschreiben Sie das Ereignis, dessen Wahrscheinlichkeit im Sachzusammenhang mit dem Term \(0{,}09 \cdot 0{,}15 + 0{,}91 \cdot 0{,}35\) berechnet wird.
(2 BE)
Lösung zu Teilaufgabe 3c
Pfadregeln, Verknüpfung von Ereignissen
\[0{,}09 \cdot 0{,}15 + 0{,}91 \cdot 0{,}35\]
\(T\): „Das Testergebnis ist positiv."
\(\overline{T}\): „Das Testergebnis ist negativ."
\(A\): „Person leidet an einer Tierhaarallergie."
\(\overline{A}\): „Person leidet nicht an einer Tierhaarallergie."
Mithilfe der bekannten Wahrscheinlichkeiten \(P(A)\), \(P_{A}(T)\) und \(P_{\overline{A}}(T)\) (vgl. Teilaufgabe a) lässt sich ein vollständig beschriftetes Baumdiagramm anfertigen.
\(P(A) = 0{,}09\), \(P_{A}(T) = 0{,}85\), \(P_{\overline{A}}(T) = 0{,}35\)
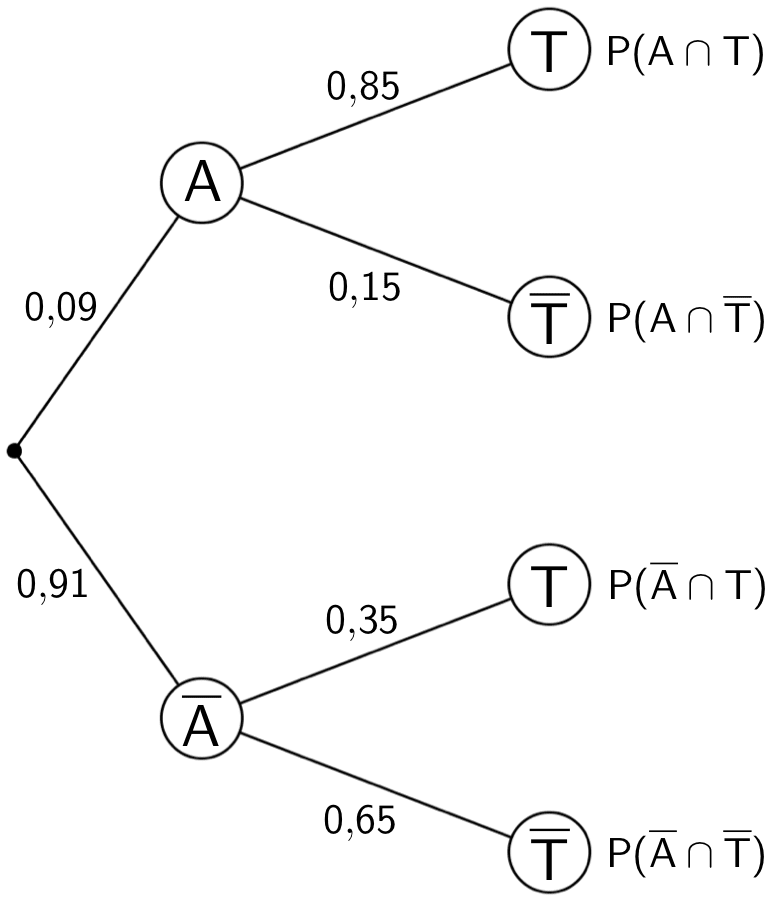
Baumdiagramm mit den Eintragungen der Wahrscheinlichkeiten an allen Pfaden
Wahrscheinlichkeiten bzw. Ereignisse zuordnen:
Unter Anwendung der 1. Pfadregel können die Wahrscheinlichkeiten zugeordnet werden.
Pfadregeln
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu diesem Ereignis gehören.
\[\begin{align*}0{,}09 \cdot 0{,}15 + 0{,}91 \cdot 0{,}35 &= P(A \cap \overline{T}) + P(\overline{A} \cap T) \\[0.8em] &= P\left[ (A \cap \overline{T}) \cup (\overline{A} \cap T) \right] \end{align*}\]
Der Term \(0{,}09 \cdot 0{,}15 + 0{,}91 \cdot 0{,}35\) beschreibt die Wahrscheinlichkeit des Ereignisses \((A \cap \overline{T}) \cup (\overline{A} \cap T)\).
Bedeutung im Sachzusammenhang:
Die Aufgabenstellung zu Aufgabe 3 (vgl. Teilaufgabe 3a) beschreibt einen Hauttest (Allergietest).
Das Ereignis \((A \cap \overline{T}) \cup (\overline{A} \cap T)\) bedeutet:
„Eine zufällig ausgewählte Person aus der Bevölkerung Deutschlands
- leidet entweder an einer Tierhaarallergie und das Testergebnis ist negativ oder sie
- leidet nicht an einer Tierhaarallergie und das Testergebnis ist positiv."
Folglich beschreibt der Term \(0{,}09 \cdot 0{,}15 + 0{,}91 \cdot 0{,}35\) im Sachzusammenhang die Wahrscheinlichkeit dafür, dass der Allergietest ein falsches Ergebnis liefert.


