Die Abbildung zeigt Daten zu den Rauchergewohnheiten der Bevölkerung Deutschlands, die das Statistische Bundesamt auf der Grundlage einer repräsentiven statistischen Erhebung veröffentlicht hat.
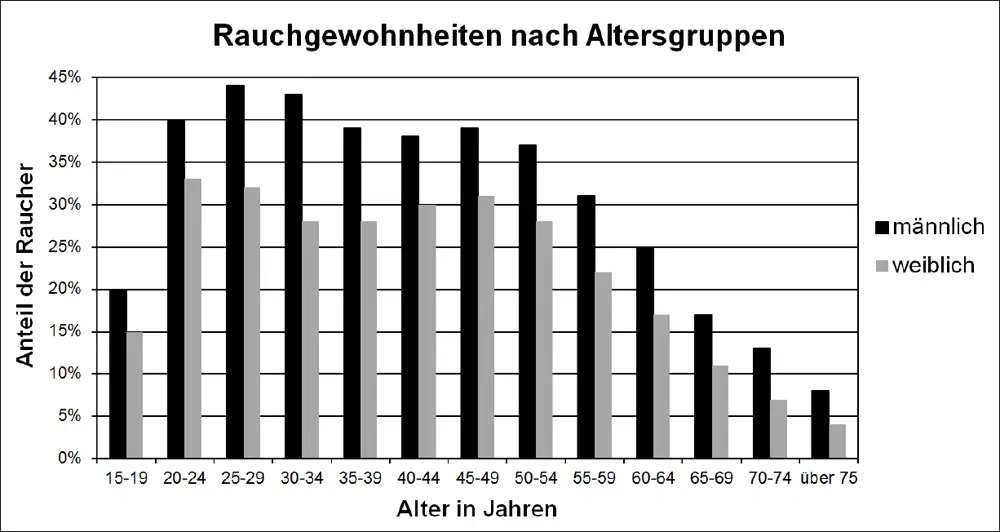
Der Abbildung lässt sich beispielsweise entnehmen, dass 17 % der 65- bis 69-jährigen Männer rauchen. Somit kann im Folgenden davon ausgegangen werden, dass die Wahrscheinlichkeit dafür, dass ein zufällig ausgewählter Mann aus dieser Altersgruppe raucht, 17 % beträgt.
Bestimmen Sie die Wahrscheinlichkeit dafür, dass ein zufällig ausgewählter 25- bis 29-jähriger Mann Nichtraucher ist.
(2 BE)
Lösung zu Teilaufgabe 1a
Ereignisse:
\(R\): "Raucher"
\(\overline R\): "Nichtraucher"
\(M\): "männlich"
\(W\): "weiblich" (\(W = \overline{M}\))
Aus dem Diagramm abzulesen:
\[P(25-29, M, R) \approx 44 \; \%\]
Betrachten des Gegenereignisses:
\[\begin{align*} P(25-29, M, \overline R) &= 1 - P(25-29, M, R) \\[0.8em] &= 1 - 0{,}44 \\[0.8em] &= 0{,}56 = 56 \; \% \end{align*}\]
Die Wahrscheinlichkeit, dass ein zufällig ausgewählter 25-29-jähriger Mann Nichtraucher ist, beträgt 56 %.


