Mathematik Klausur Q11/1-002 Bayern
Aufgabe 1
Bestimmen Sie die Ableitungsfunktion \(f'\) der Funktion \(f \colon x \mapsto (3x - 2)(x + 1) - \dfrac{1}{x}\) und vereinfachen Sie den Term.
Aufgabe 2
Gegeben ist die Funktion \(f \colon x \mapsto \dfrac{3x^{2} + 3x - 6}{{(x + 1)}^{2}}\) mit dem maximalen Definitionsbereich \(D_{f}\). Der Graph der Funktion \(f\) wird mit \(G_{f}\) bezeichnet.
a) Geben Sie \(D_{f}\) an.
b) Ermitteln Sie die Koordinaten aller Schnittpunkte von \(G_{f}\) mit den Koordinatenachsen.
c) Untersuchen Sie das Verhalten der Funktion \(f\) an den Rändern des Definitionsbereichs.
d) Stellen Sie die Gleichung der Tangente \(T\) an \(G_{f}\) sowie die Gleichung der Normalen \(N\) an der Stelle \(x = 1\) auf.
e) Zeichnen Sie \(G_{f}\), die Tangente \(T\) und die Normale \(N\) unter Berücksichtigung der bisherigen Ergebnisse in ein geeignetes Koordinatensystem.
f) Bestimmen Sie den Flächeninhalt des Dreiecks, welches die Tangente \(T\) und die Normale \(N\) mit der \(y\)-Achse bilden.
Aufgabe 3
Gegeben ist die in \(\mathbb R\) definierte Funktion \(f \colon x \mapsto -\dfrac{1}{8}x^{3} + \dfrac{3}{2}x^{2} - \dfrac{9}{2}x\). Der Graph der Funktion \(f\) wird mit \(G_{f}\) bezeichnet.
Untersuchen Sie das Monotonieverhalten der Funktion \(f\) und geben Sie die Lage und die Art der lokalen Extrempunkte von \(G_{f}\) an.
Aufgabe 4
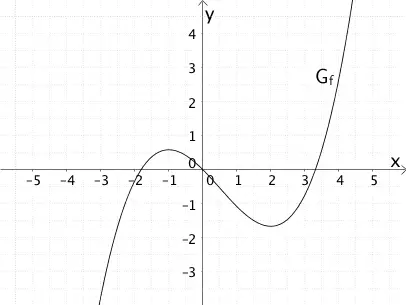
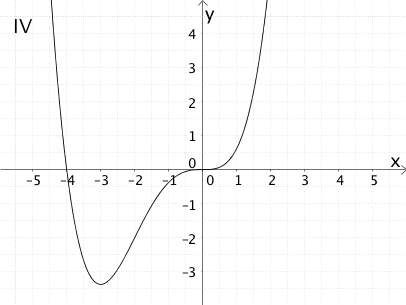
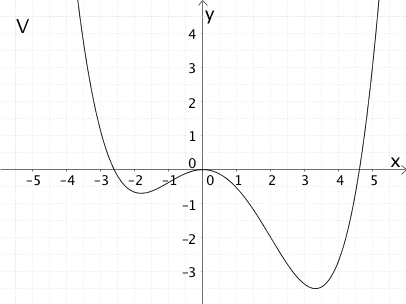
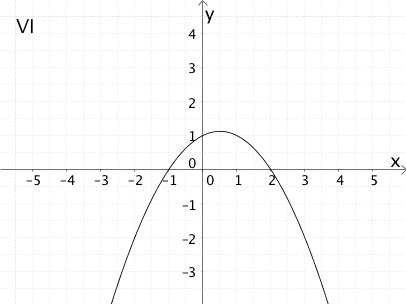
Die Abbildung zeigt den Graphen \(G_{f}\) einer Funktion \(f\).
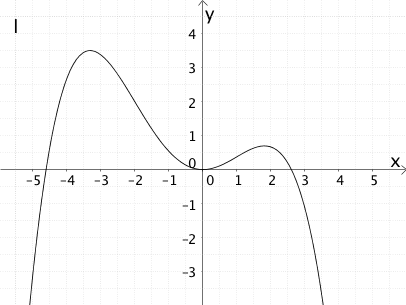
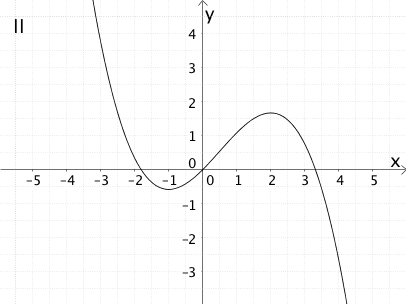
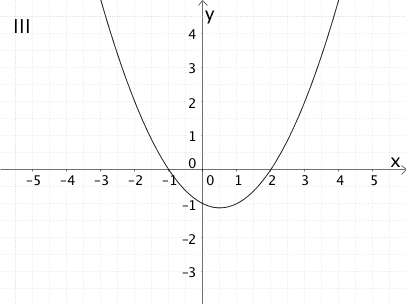
Ordnen Sie dem Graphen der Funktion \(f\) aus den Graphen I bis VI den Graphen der zugehörigen Ableitungsfunktion \(f'\) und einer zugehörigen Stammfunktion \(F\) zu. Begründen Sie Ihre Wahl.
Aufgabe 5
Gegeben ist die Funktion \(f \colon x \mapsto 3x + 2 + \dfrac{1}{x^{2}}\). Der Graph der Funktion \(f\) wird mit \(G_{f}\) bezeichnet.
a) Untersuchen Sie das Symmetrieverhalten von \(G_{f}\) bzgl. des Koordinatensystems.
b) Geben Sie die Art und die Gleichungen aller Asymptoten der Funktion \(f\) an.
c) Geben Sie eine Stammfunktion der Funktion \(f\) an.
Aufgabe 6
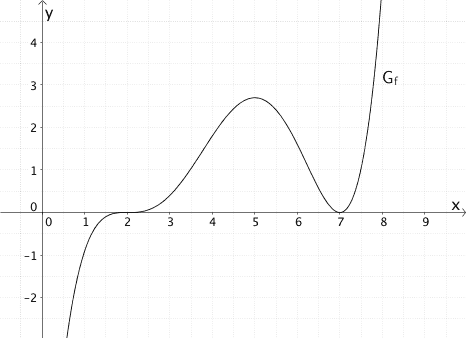
Die Abbildung zeigt den Graphen \(G_{f}\) einer Funktion \(f\). Die Ableitungsfunktion von \(f\) wird mit \(f'(x)\) bezeichnet, eine Stammfunktion von \(f\) wird mit \(F(x)\) bezeichnet.
Entscheiden Sie jeweils, ob die nachfolgenden Aussagen richtig oder falsch sind und begründen Sie Ihre Entscheidung.
a) \(f'(x)\) hat genau zwei Nullstellen.
b) \(f'(x) < 0\) für \(5{,}5 < x < 6{,}5\)
c) \(f'(6) > f'(7)\)
d) \(f'(4) \approx f'(6)\)
e) Der Graph von \(F(x)\) hat an der Stelle \(x = 6\) in etwa die Steigung \(-1\).
f) Der Graph von \(F(x)\) hat an der Stelle \(x = 7\) einen Terrassenpunkt.
- Details
- Hauptkategorie: Klausuren Q11/1
Bestimmen Sie die Ableitungsfunktion \(f'\) der Funktion \(f \colon x \mapsto (3x - 2)(x + 1) - \dfrac{1}{x}\) und vereinfachen Sie den Term.
- Details
- Hauptkategorie: Klausuren Q11/1
Gegeben ist die Funktion \(f \colon x \mapsto \dfrac{3x^{2} + 3x - 6}{{(x + 1)}^{2}}\) mit dem maximalen Definitionsbereich \(D_{f}\). Der Graph der Funktion \(f\) wird mit \(G_{f}\) bezeichnet.
a) Geben Sie \(D_{f}\) an.
b) Ermitteln Sie die Koordinaten aller Schnittpunkte von \(G_{f}\) mit den Koordinatenachsen.
c) Untersuchen Sie das Verhalten der Funktion \(f\) an den Rändern des Definitionsbereichs.
d) Stellen Sie die Gleichung der Tangente \(T\) an \(G_{f}\) sowie die Gleichung der Normalen \(N\) an der Stelle \(x = 1\) auf.
e) Zeichnen Sie \(G_{f}\), die Tangente \(T\) und die Normale \(N\) unter Berücksichtigung der bisherigen Ergebnisse in ein geeignetes Koordinatensystem.
f) Bestimmen Sie den Flächeninhalt des Dreiecks, welches die Tangente \(T\) und die Normale \(N\) mit der \(y\)-Achse bilden.
- Details
- Hauptkategorie: Klausuren Q11/1
Gegeben ist die in \(\mathbb R\) definierte Funktion \(f \colon x \mapsto -\dfrac{1}{8}x^{3} + \dfrac{3}{2}x^{2} - \dfrac{9}{2}x\). Der Graph der Funktion \(f\) wird mit \(G_{f}\) bezeichnet.
Untersuchen Sie das Monotonieverhalten der Funktion \(f\) und geben Sie die Lage und die Art der lokalen Extrempunkte von \(G_{f}\) an.
- Details
- Hauptkategorie: Klausuren Q11/1
Die Abbildung zeigt den Graphen \(G_{f}\) einer Funktion \(f\).
Ordnen Sie dem Graphen der Funktion \(f\) aus den Graphen I bis VI den Graphen der zugehörigen Ableitungsfunktion \(f'\) und einer zugehörigen Stammfunktion \(F\) zu. Begründen Sie Ihre Wahl.
- Details
- Hauptkategorie: Klausuren Q11/1
Gegeben ist die Funktion \(f \colon x \mapsto 3x + 2 + \dfrac{1}{x^{2}}\). Der Graph der Funktion \(f\) wird mit \(G_{f}\) bezeichnet.
a) Untersuchen Sie das Symmetrieverhalten von \(G_{f}\) bzgl. des Koordinatensystems.
b) Geben Sie die Art und die Gleichungen aller Asymptoten der Funktion \(f\) an.
c) Geben Sie eine Stammfunktion der Funktion \(f\) an.
- Details
- Hauptkategorie: Klausuren Q11/1
Die Abbildung zeigt den Graphen \(G_{f}\) einer Funktion \(f\). Die Ableitungsfunktion von \(f\) wird mit \(f'(x)\) bezeichnet, eine Stammfunktion von \(f\) wird mit \(F(x)\) bezeichnet.
Entscheiden Sie jeweils, ob die nachfolgenden Aussagen richtig oder falsch sind und begründen Sie Ihre Entscheidung.
a) \(f'(x)\) hat genau zwei Nullstellen.
b) \(f'(x) < 0\) für \(5{,}5 < x < 6{,}5\)
c) \(f'(6) > f'(7)\)
d) \(f'(4) \approx f'(6)\)
e) Der Graph von \(F(x)\) hat an der Stelle \(x = 6\) in etwa die Steigung \(-1\).
f) Der Graph von \(F(x)\) hat an der Stelle \(x = 7\) einen Terrassenpunkt.
- Details
- Hauptkategorie: Klausuren Q11/1
2023 Christian Rieger・mathelike
