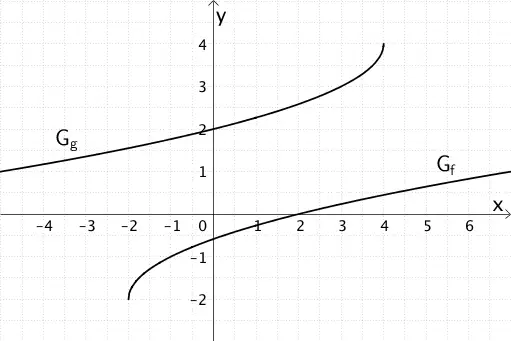
Die Abbildung zeigt je einen Ausschnitt des Graphen \(G_{f}\) der Funktion \(f \colon x \mapsto \sqrt{x + 2} - 2\) und des Graphen \(G_{g}\) der Funktion \(g \colon x \mapsto -\sqrt{4 - x} + 4\).
a) Beschreiben Sie schrittweise wie der Graph \(G_{f}\) und der Graph \(G_{g}\) jeweils aus dem Graphen der Funktion \(x \mapsto \sqrt{x}\) hervorgeht und bestimmen Sie jeweils die maximale Definitionsmenge der Funktionen \(f\) und \(g\) durch Rechnung.
Betrachtet wird die Strecke \([PQ]\) der Punkte \(P(x|f(x))\) und \(Q(x|g(x))\) mit derselben Abszisse.
b) Zeigen Sie, dass der Funktionsterm \(d(x) = -\sqrt{4 - x} -\sqrt{x + 2} + 6\) die Länge der Strecke \([PQ]\) in Abhängigkeit der \(x\)-Koordinate des Punktes \(P\) bzw. \(Q\) beschreibt, und geben Sie die Definitionsmenge der Funktion \(d\) an.
c) Bestimmen Sie die \(x\)-Koordinate des Punktes \(P\) bzw. \(Q\), für die die Länge der Strecke \([PQ]\) minimal ist.
Die Gerade \(x = -1\) und die Gerade \(x = 3\) schließen mit den Graphen \(G_{f}\) und \(G_{g}\) ein Flächenstück mit dem Flächeninhalt \(A\) ein.
d) Der Flächeninhalt \(A\) soll zunächst näherungsweise berechnet werden. Hierfür wird das Viereck \(SPQR\) betrachtet, welches die Punkte \(S(-1|f(-1))\), \(P(3|f(3))\), \(Q(3|g(3))\) und \(R(-1|g(-1))\) festlegen. Der Schnittpunkt der Strecken \([PR]\) und \([QS]\) halbiert die Strecken jeweils.
Zeichnen Sie das Viereck \(SPQR\) in die Abbildung ein und schraffieren Sie das Flächenstück mit dem Flächeninhalt \(A\). Beschreiben Sie die wesentlichen Schritte eines geeigneten Lösungsverfahrens, um \(A\) näherungsweise zu berechnen.
e) Berechnen Sie den exakten Wert des Flächeninhalts \(A\).
f) Betrachtet wird nun die Integralfunktion \(\displaystyle I \colon x \mapsto \int_{0}^{x} d(t) dt\).
Geben Sie an, welche der folgenden Terme die Maßzahl des Flächeninhalts \(A\) berechnen (Falsche Antworten zählen negativ).
(I) \(I(-1) + I(3)\)
(II) \(I(-1) - I(3)\)
(III) \(I(3) - I(-1)\)
(IV) \(\vert I(-1) \vert - \vert I(3) \vert\)
(V) \(\vert I(-1) \vert + I(3)\)
(VI) \(I(-1) + \vert I(3) \vert\)
a) Entstehung von \(G_{f}\) und \(G_{g}\) aus dem Graphen der Funktion \(x \mapsto \sqrt{x}\) sowie maximale Definitionsmenge der Funktionen \(f\) und \(g\)
Entstehung von \(G_{f}\) aus dem Graphen der Funktion \(x \mapsto \sqrt{x}\)
\[f(x) = \sqrt{x + 2} - 2\]
1. Verschiebung um 2 LE (Längeneinheiten) in Richtung der negativen \(x\)-Achse:
Verschieben von Funktionsgraphen
\[g(x) = f(x +a) + b\]
Verschiebung in \(x\)-Richtung um \(-a\), Verschiebung in \(y\)-Richtung um \(b\)
\[\Longrightarrow \quad x \mapsto \sqrt{x + 2}\]
2. Verschiebung um 2 LE in Richtung der negativen \(y\)-Achse:
\[\Longrightarrow \quad x \mapsto \sqrt{x + 2} - 2 = f(x)\]
Anmerkung:
Die Reihenfolge der vorgestellten Schritte lässt sich umkehren.
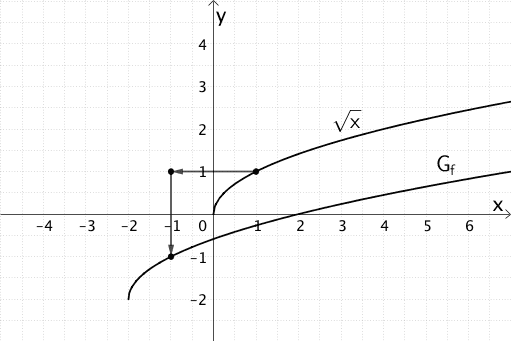
Veranschaulichung: Entstehung des Graphen \(G_{f}\) aus dem Graphen der Funktion \(x \mapsto \sqrt{x}\)
Entstehung von \(G_{g}\) aus dem Graphen der Funktion \(x \mapsto \sqrt{x}\)
Anmerkung:
Die Reihenfolge der nachfolgend vorgestellten Schritte versteht sich als Beispiel.
\[g(x) = -\sqrt{4 - x} + 4\]
1. Spiegelung an der \(x\)-Achse:
Spiegeln von Funktionsgraphen
Spiegelung an der \(x\)-Achse: \(g(x) = -f(x)\)
Spiegelung an der \(y\)-Achse: \(h(x) = f(-x)\)
\[\Longrightarrow \quad x \mapsto -\sqrt{x}\]
2. Spiegelung an der \(y\)-Achse:
\[\Longrightarrow \quad x \mapsto -\sqrt{-x}\]
3. Verschiebung um 4 LE in Richtung der positiven \(x\)-Achse:
Verschieben von Funktionsgraphen
\[g(x) = f(x +a) + b\]
Verschiebung in \(x\)-Richtung um \(-a\), Verschiebung in \(y\)-Richtung um \(b\)
\[\Longrightarrow \quad x \mapsto -\sqrt{-(x - 4)} = -\sqrt{4 - x}\]
4. Verschiebung um 4 LE in Richtung der positiven \(y\)-Achse:
\[\Longrightarrow \quad x \mapsto -\sqrt{4 - x} + 4 = g(x)\]
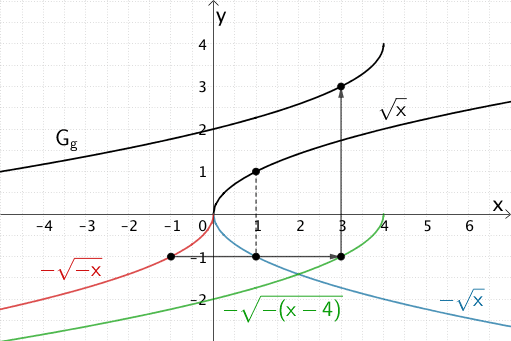
Veranschaulichung: Entstehung des Graphen \(G_{g}\) aus dem Graphen der Funktion \(x \mapsto \sqrt{x}\)
Maximale Definitionsmenge der Funktionen \(f\) und \(g\)
\[f(x) = \sqrt{x + 2} - 2\]
\[g(x) = -\sqrt{4 - x} + 4\]
Der Radikand (Ausdruck unter der Wurzel) darf nicht negativ sein.
\[\begin{align*}x + 2 &\geq 0 & &| -2 \\[0.8em] x &\geq -2 \end{align*}\]
\[\Longrightarrow \quad D_{f} = [-2;+\infty[\]
\[\begin{align*}4 - x &\geq 0 & &| +x \\[0.8em] 4 &\geq x \end{align*}\]
\[\Longrightarrow \quad D_{g} = \;]-\infty;4]\]
b) Nachweis, dass der Funktionsterm \(d(x) = -\sqrt{4 - x} -\sqrt{x + 2} + 6\) die Länge der Strecke \([PQ]\) beschreibt und Definitionsmenge der Funktion \(d\)
![Strecke [PQ] der Punkte P(x|f(x)) und Q(x|g(x)) Strecke [PQ] der Punkte P(x|f(x)) und Q(x|g(x))](/images/stories/Klausuren/Klausuren_Q12_2/Klausur_Q12_2-001/Klausur_Q12_2-001_A1b.png)
Da die Punkte \(P(x|f(x))\) und \(Q(x|g(x))\) dieselbe Abszisse haben, d.h. der \(x\)-Wert der Punkte ist stets derselbe, ergibt sich die Länge der Strecke \([PQ]\) als die Differenz der \(y\)-Werte der Punkte \(P\) und \(Q\) mit \(y_{Q} > y_{P}\).
\[f(x) = \sqrt{x + 2} - 2; \; D_{f} = [-2;+\infty[\]
\[g(x) = -\sqrt{4 - x} + 4; \; D_{g} = \;]-\infty;4]\]
\[\begin{align*} \overline{PQ}(x) &= y_{Q} - y_{P} \\[0.8em] &= g(x) - f(x) \\[0.8em] &= -\sqrt{4 - x} + 4 - \left(\sqrt{x + 2} - 2\right) \\[0.8em] &= -\sqrt{4 - x} + 4 - \sqrt{x + 2} + 2 \\[0.8em] &= -\sqrt{4 - x} - \sqrt{x + 2} + 6 \\[0.8em] &= d(x) \end{align*}\]
Die Grenzen der maximalen Definitionsmengen \(D_{f}\) und \(D_{g}\) der Funktionen \(f\) und \(g\) legen die Definitionsmenge der Funktion \(d\) fest.
\[d(x) = -\sqrt{4 - x} - \sqrt{x + 2} + 6; \; D_{d} = [-2;4]\]
c) Bestimmung der \(x\)-Koordinate des Punktes \(P\) bzw. \(Q\), für die die Länge der Strecke \([PQ]\) minimal ist
(vgl. Abiturskript - 1.5.7 Extremwertaufgaben)
Aus Teilaufgabe b ist bekannt, dass der Funktionsterm \(d(x)\) für \(x \in [-2;4]\) die Länge der Strecke \([PQ]\) in Abhängigkeit der \(x\)-Koordinate des Punktes \(P\) bzw. \(Q\) beschreibt.
Folglich lautet die notwendige Bedingung für die minimale Länge der Strecke \([PQ]\):
\[d'(x) = 0\]
Erste Ableitung \(d'\) bilden:
Die erste Ableitung \(d'\) der Funktion \(d\) lässt sich mithilfe der Ableitung einer Wurzelfunktion, der Kettenregel, der Ableitung einer Potenzfunktion sowie der Summen- und der Faktorregel bilden. Als Alternative kann \(d(x)\) zunächst mithilfe der Rechenregel für Potenzen \(\sqrt[n]{a^{m}} = a^{\frac{m}{n}}\) in der Potenzschreibweise formuliert werden.
\[d(x) = -\sqrt{4 - x} - \sqrt{x + 2} + 6 = -(4 - x)^{\frac{1}{2}} - (x + 2)^{\frac{1}{2}} + 6\]
1. Möglichkeit (ohne Formulierung in der Potenzschreibweise):
\[d(x) = -\sqrt{4 - x} - \sqrt{x + 2} + 6\]
Ableitung einer Wurzelfunktion
\[f(x) = \sqrt{g(x)} \quad \Longrightarrow \quad f'(x) = \frac{g'(x)}{2\sqrt{g(x)}} \quad (g(x) \geq 0)\]
Kettenregel
\[f(x) = u(v(x)) \quad \Longrightarrow \quad f'(x) = u'(v(x)) \cdot v'(x) \]
Ableitung einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
Faktorregel
\(f(x) = a \cdot u(x) \quad \Longrightarrow \quad f'(x) = a \cdot u'(x)\)
Summenregel
\(f(x) = u(x) + v(x) \quad \Longrightarrow \quad f'(x) = u'(x) + v'(x)\)
(vgl. Merkhilfe)
\[\begin{align*} d'(x) &= (-1) \cdot \frac{-1}{2\sqrt{4 - x}} - \frac{1}{2\sqrt{x + 2}} + 0 \\[0.8em] &= \frac{1}{2\sqrt{4 - x}} - \frac{1}{2\sqrt{x + 2}} & &| \; \text{gemeinsamen Nenner bilden} \\[0.8em] &= \frac{\sqrt{x + 2}}{2\sqrt{4 - x}\sqrt{x + 2}} - \frac{\sqrt{4 - x}}{2\sqrt{4 - x}\sqrt{x + 2}} \\[0.8em] &= \frac{\sqrt{x + 2} - \sqrt{4 - x}}{2\sqrt{4 - x}\sqrt{x + 2}} \end{align*}\]
2. Möglichkeit (nach Formulierung in der Potenzschreibweise):
\[d(x) = -(4 - x)^{\frac{1}{2}} - (x + 2)^{\frac{1}{2}} + 6\]
Ableitung einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
Kettenregel
\[f(x) = u(v(x)) \quad \Longrightarrow \quad f'(x) = u'(v(x)) \cdot v'(x) \]
Faktorregel
\(f(x) = a \cdot u(x) \quad \Longrightarrow \quad f'(x) = a \cdot u'(x)\)
Summenregel
\(f(x) = u(x) + v(x) \quad \Longrightarrow \quad f'(x) = u'(x) + v'(x)\)
(vgl. Merkhilfe)
\[\begin{align*} d'(x) &= (-1) \cdot \frac{1}{2}(4 - x)^{-\frac{1}{2}} \cdot (-1) -\frac{1}{2}(x + 2)^{-\frac{1}{2}} + 0 &&| \; a^{-n} = \frac{1}{a^{n}}; \; a^{\frac{m}{n}} = \sqrt[n]{a^{m}} \\[0.8em] &= \frac{1}{2\sqrt{4 - x}} - \frac{1}{2\sqrt{x + 2}} & &| \; \text{gemeinsamen Nenner bilden} \\[0.8em] &= \frac{\sqrt{x + 2}}{2\sqrt{4 - x}\sqrt{x + 2}} - \frac{\sqrt{4 - x}}{2\sqrt{4 - x}\sqrt{x + 2}} \\[0.8em] &= \frac{\sqrt{x + 2} - \sqrt{4 - x}}{2\sqrt{4 - x}\sqrt{x + 2}} \end{align*}\]
Nullstelle(n) von \(d'\) berechnen:
\[\begin{align*} d'(x) &= 0 \\[0.8em] \frac{\sqrt{x + 2} - \sqrt{4 - x}}{2\sqrt{4 - x}\sqrt{x + 2}} &= 0 \end{align*}\]
Ein Bruch ist gleich Null, wenn der Zähler gleich Null ist.
\[\begin{align*} \Longrightarrow \quad \sqrt{x + 2} - \sqrt{4 - x} &= 0 &&| + \sqrt{4 - x}\; \text{(Wurzeln isolieren)} \\[0.8em] \sqrt{x + 2} &= \sqrt{4 - x} &&| \; (\dots)^{2} \; \text{(Quadrieren)} \\[0.8em] x + 2 &= 4 - x &&| + x - 2 \\[0.8em] 2x &= 2 &&| : 2 \\[0.8em] x &= 1 \end{align*}\]
Für \(x = 1\) ist die Länge der Strecke \([PQ]\) extremal.
Nachweis, dass die Länge der Strecke \([PQ]\) für \(x = 1\) minimal ist:
Die Länge der Strecke \([PQ]\) ist für \(x = 1\) minimal, wenn \(d(1)\) ein relatives Minimum ist, d.h. wenn d'(x) an der Stelle \(x = 1\) das Vorzeichen von \(-\) nach \(+\) wechselt (vgl. Abiturskript - 1.5.3 Monotonieverhalten, Extrem- und Terrassenpunkte).
\[d'(x) = \frac{\sqrt{x + 2} - \sqrt{4 - x}}{\underbrace{2\sqrt{4 - x}\sqrt{x + 2}}_{>\,0}}\]
Der Zählerterm \(\sqrt{x + 2} - \sqrt{4 - x}\) bestimmt den Vorzeichenwechsel von \(d'(x)\) an der Stelle \(x = 1\).
Beispielsweise ergibt sich für \(x = 0\)
\[\sqrt{0 + 2} - \sqrt{4 - 0} = \sqrt{2} - 2 \quad \Longrightarrow \quad d'(0) < 0\]
und für \(x = 2\)
\[\sqrt{2 + 2} - \sqrt{4 - 2} = 2 - \sqrt{2} \quad \Longrightarrow \quad d'(2) > 0\]
Somit folgt:
\[\left. \begin{align*} &d'(x) < 0 \; \text{für} \; -2 \leq x < 1 \\[0.8em] &d'(1) = 0 \\[0.8em] &d'(x) > 0 \; \text{für} \; 1 < x \leq 4 \end{align*} \right\} \enspace \Rightarrow \text{rel. Minimum} \; d(1)\]
Veranschaulichung mithilfe einer Vorzeichentabelle:
| \(x\) | \(-2 \leq x < 1\) | \(1\) | \(1 < x \leq 4\) |
| \(\sqrt{x + 2} - \sqrt{4 - x}\) | \(-\) | \(0\) | \(+\) |
| \(d'(x)\) | \(-\) | \(0\) | \(+\) |
| rel. Minimum \(d(1)\) |
Berücksichtigung möglicher Randminima:
(vgl. Abiturskript - 1.5.7 Extremwertaufgaben)
An den Ränder des Definitionsbereichs \(D_{d} = [-2;4]\) ist die Funktion \(d\) nicht differenzierbar (nicht ableitbar), da einmal der linksseitige Differentialquotient \(\lim \limits_{x\,\to\,-2^{-}} \dfrac{d(x) - d(-2)}{x + 2}\) und einmal der rechtsseitige Differentialquotient \(\lim \limits_{x\,\to\,4^{+}} \dfrac{d(x) - d(4)}{x - 4}\) nicht existiert (vgl. Abiturskript - 1.5.1 Die Ableitung, Differenzierbarkeit).
Differenzierbarkeit
Existiert für eine Funktion \(f\) an der Stelle \(x_0\) der Differentialquotient
\(\displaystyle f'(x_0) \, = \, \lim \limits_{x\,\to\,x_0} \frac{f(x) - f(x_0)}{x - x_0} \, = \, \lim \limits_{h\,\to\,0} \frac{f(x_0 + h) - f(x_0)}{h}\,\),
heißt die Funktion \(f\) differenzierbar an der Stelle \(\bf{x_0}\).
Der Differentialquotient existiert, wenn der linksseitige Grenzwert des Differentialquotienten (\(\underset{\textcolor{#cc071e}{x\,<\,x_0}}{x\,\to\,x_0}\) bzw. \(\underset{\textcolor{#cc071e}{h\,<\,0}}{h\,\to\,0}\)) und der rechtsseitige Grenzwert des Differentialquotienten (\(\underset{\textcolor{#0087c1}{x\,>\,0}}{x\,\to\,x_0}\) bzw. \(\underset{\textcolor{#0087c1}{h\,>\,0}}{h\,\to\,0}\)) übereinstimmen.
Das bedeutet, dass die Anwendung der Differentialrechnung \((d'(x) = 0)\) mögliche Randminima nicht erfasst, und deshalb der Funktionswert \(d(1)\) mit den Funktionswerten \(d(-2)\) und \(d(4)\) gesondert zu vergleichen ist.
\[d(x) = -\sqrt{4 - x} - \sqrt{x + 2} + 6; \; D_{d} = [-2;4]\]
\[d(1) = -\sqrt{4 - 1} - \sqrt{1 + 2} + 6 = -2\sqrt{3} + 6 \approx 2{,}54\]
\[d(-2) = -\sqrt{4 - (-2)} - \sqrt{-2 + 2} + 6 = -\sqrt{6} + 6 \approx 3{,}55\]
\[d(4) = -\sqrt{4 - 4} - \sqrt{4 + 2} + 6 = -\sqrt{6} + 6 \approx 3{,}55\]
\[\Longrightarrow \quad d(1) < d(-2) \; \wedge \; d(1) < d(4)\]
Es existieren keine Randminima. Also ist die Länge der Strecke \([PQ]\) für \(x = 1\) mit ca 2,54 LE (Längeneinheiten) minimal.
d) Näherungsweise Berechnung des Flächeninhalts \(A\)
Einzeichnen des Vierecks \(SPQR\) und schraffieren des Flächenstücks mit dem Flächeninhalt \(A\)
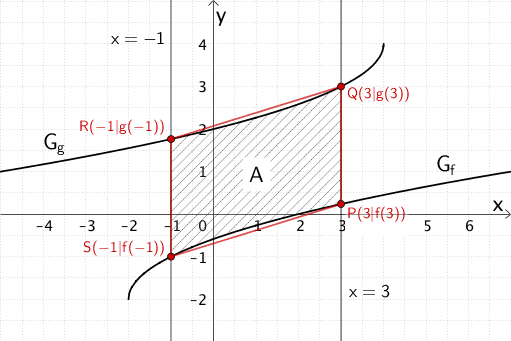
Flächeninhalt \(A\) des Flächenstücks, das die Geraden \(x = -1\) und \(x = 3\) mit den Graphen \(G_{f}\) und \(G_{g}\) einschließen. Viereck \(SPQR\), das die Punkte \(S(-1|f(-1))\), \(P(3|f(3))\), \(Q(3|g(3))\) und \(R(-1|g(-1))\) festlegen.
Beschreibung der wesentlichen Schritte eines geeigneten Lösungsverfahrens, um \(A\) näherungsweise zu berechnen
1. Möglichkeit: Flächeninhalt des Vierecks \(SPQR\)
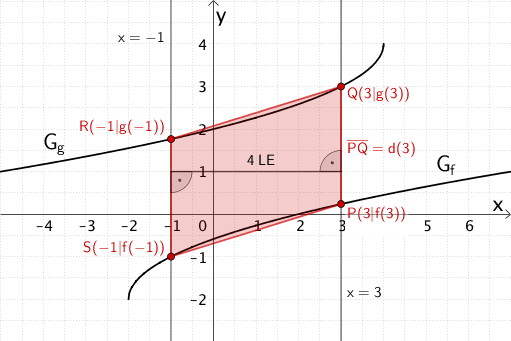
In der Aufgabenstellung heißt es: „Der Schnittpunkt der Strecken \([PR]\) und \([QS]\) halbiert die Strecken jeweils." Daraus lässt sich schlussfolgern, dass das Viereck \(SPQR\) ein Parallelogramm ist.
Anmerkung:
Ein Viereck ist ein Parallelogramm, wenn die Diagonalen einander halbieren, die Sonderformen eines Parallelogramms - Raute, Rechteck und Quadrat - mit eingeschlossen.
Für den Flächeninhalt eines Parallelogramms gilt:
\[A_{\text{Parallelogramm}} = g \cdot h\]
Dabei bedeutet \(g\) die Länge einer betrachteten Grundlinie und \(h\) die Höhe, d.h. den Abstand der betrachteten (parallelen) Grundlinien.
Wählt man nun beispielsweise die Strecke \([PQ]\) als Grundlinie und den Abstand \(d([PQ];[RS])\) der parallelen Strecken \([PQ]\) und \([SR]\) als Höhe des Parallelogramms \(SPQR\), so lässt sich die Maßzahl des Flächeninhalts \(A\) näherungsweise wie folgt berechnen:
\[\begin{align*} A &\approx A_{SPQR} \\[0.8em] &= \overline{PQ} \cdot d([PQ];[RS]) \\[0.8em] &= d(3) \cdot (x_{P} - x_{S}) \\[0.8em] &= d(3) \cdot (3 - (-1)) \\[0.8em] &= d(3) \cdot 4 \end{align*}\]
2. Möglichkeit: „Kästchen zählen"
Die Methode „Kästchen zählen" kann unabhängig von der in der Aufgabenstellung genannten Betrachtung des Vierecks \(SPQR\) angewendet werden.
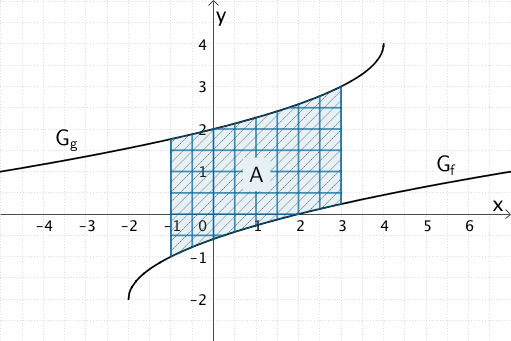
Das Flächenstück mit dem Flächeninhalt \(A\) lässt sich in ca. 41 „Kästchen" unterteilen. Der Flächeninhalt eines „Kästchens" beträgt \(0{,}25\) FE (Flächeneinheiten).
Somit ergibt sich die Maßzahl des Flächeninhalt \(A\) näherungsweise zu:
\[A \approx 41 \cdot 0{,}25 = 10{,}25\]
e) Berechnung des exakten Werts des Flächeninhalts \(A\)
(vgl. Abiturskript - 1.6.4 Flächenberechnung, Flächeninhalt zwischen zwei Funktionsgraphen)
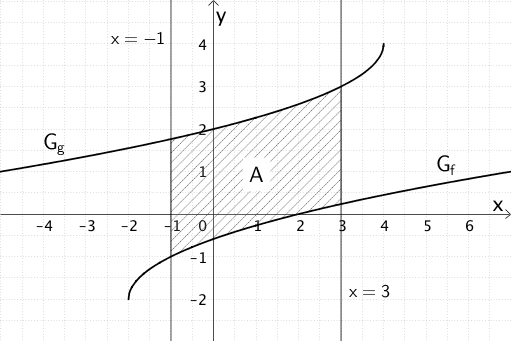
Es ist der Flächeninhalt zwischen den Graphen der Funktionen \(f\) und \(g\) im Intervall \([-1;3]\) zu berechnen, wobei der Abbildung zu entnehmen ist, dass im betrachteten Intervall \(g(x) > f(x)\) gilt.
Es wird also über die Differenzfunktion \(g(x) - f(x)\) integriert. Mit \(g(x) > f(x)\) kann auf den Betrag des Integrals verzichtet werden.
In Teilaufgabe b wurde gezeigt, dass der Funktionsterm \(d(x)\) die Differenzfunktion \(g(x) - f(x)\) beschreibt.
\[\begin{align*}A &= \int_{-1}^{3} \left[ g(x) - f(x) \right] dx \\[0.8em] &= \int_{-1}^{3} d(x) dx \\[0.8em] &= \int_{-1}^{3} \left( -\sqrt{4 - x} - \sqrt{x + 2} + 6 \right)dx \end{align*}\]
Berechnung bestimmter Integrale
\[\int_{a}^{b} f(x)\,dx = [F(x)]_{a}^{b} = F(b) - F(a)\]
Dabei ist \(F\) eine beliebige Stammfunktion zu \(f\).
(vgl. Merkhilfe)
Eigenschaften des bestimmten Integrals - Integrationsregeln
Identische Integrationsgrenzen:
\[\int_{a}^{a} f(x)\,dx = 0\]
Faktorregel:
\(\displaystyle \int_{a}^{b} c \cdot f(x)\,dx = c \cdot \int_{a}^{b} f(x)\,dx\) mit \(c \in \mathbb R\)
Summenregel:
\[\int_{a}^{b} \left[f(x) \pm g(x) \right] dx = \int_{a}^{b}f(x)\,dx \pm \int_{a}^{b}g(x)\,dx\]
Vertauschungsregel:
\[\int_{a}^{b}f(x)\,dx = -\int_{b}^{a}f(x)\,dx\]
Zerlegung in Teilintervalle:
\(\displaystyle \int_{a}^{b}f(x)\,dx = \int_{a}^{c}f(x)\,dx + \int_{c}^{b}f(x)\,dx\) mit \(a \leq c \leq b\)
Für die Berechnung des bestimmten Integrals \(\displaystyle \int_{-1}^{3} d(x) dx\) wird eine Stammfunktion \(D\) der Integrandenfunktion \(d\) benötigt.
Die Menge aller Stammfunktionen der Funktion \(d\) ist gegeben durch das unbestimmte Integral \(\displaystyle \int d(x) dx\).
Zunächst wird der Funktionsterm \(d(x)\) in der Potenzschreibweise formuliert (vgl. Teilaufgabe c). Anschließend lässt sich das unbestimmte Integral \(\displaystyle \int d(x) dx\) mithilfe der wichtigen unbestimmten Integrale
\(\displaystyle \int x^r \,dx = \frac{x^{r + 1}}{r + 1} + C \; (r \neq -1)\) und
\(\displaystyle \int f(ax + b)\,dx = \frac{1}{a}F(ax +b) + C\) (wobei \(F\) eine Stammfunktion von \(f\) ist)
mit jeweils \(C \in \mathbb R\) bestimmen.
\[d(x) = -\sqrt{4 - x} - \sqrt{x + 2} + 6 = -(4 - x)^{\frac{1}{2}} - (x + 2)^{\frac{1}{2}} + 6\]
\[\begin{align*} \int d(x) dx &= \int \left[ -(4 - x)^{\frac{1}{2}} - (x + 2)^{\frac{1}{2}} + 6 \right] dx \\[0.8em] &= (-1) \cdot \underbrace{\frac{1}{-1}}_{\Large{\frac{1}{a}}} \cdot \underbrace{\frac{(4 - x)^{\frac{1}{2} + 1}}{\frac{1}{2} + 1}}_{\Large{F(ax\,+\,b)}} - \underbrace{\frac{1}{1}}_{\Large{\frac{1}{a}}} \cdot \underbrace{\frac{(x + 2)^{\frac{1}{2} + 1}}{\frac{1}{2} + 1}}_{\Large{F(ax\,+\,b)}} + 6x + C \\[0.8em] &= \frac{(4-x)^{\frac{3}{2}}}{\frac{3}{2}} - \frac{(x + 2)^{\frac{3}{2}}}{\frac{3}{2}} + 6x + C &&| \; a^{\frac{m}{n}} = \sqrt[n]{a^{m}} \\[0.8em] &= \frac{2}{3} \cdot \sqrt{(4 - x)^{3}} - \frac{2}{3} \cdot \sqrt{(x + 2)^{3}} + 6x + C \\[0.8em] &= \frac{2}{3} \left( \sqrt{(4 - x)^{3}} - \sqrt{(x + 2)^{3}} \right) + 6x + C \end{align*}\]
Für \(C = 0\) ist \(D \colon x \mapsto \frac{2}{3} \left( \sqrt{(4 - x)^{3}} - \sqrt{(x + 2)^{3}} \right) + 6x\) eine Stammfunktion der Integrandenfunktion \(d\).
Damit kann der Flächeninhalt \(A\) wie folgt berechnet werden:
Berechnung bestimmter Integrale
\[\int_{a}^{b} f(x)\,dx = [F(x)]_{a}^{b} = F(b) - F(a)\]
Dabei ist \(F\) eine beliebige Stammfunktion zu \(f\).
(vgl. Merkhilfe)
Eigenschaften des bestimmten Integrals - Integrationsregeln
Identische Integrationsgrenzen:
\[\int_{a}^{a} f(x)\,dx = 0\]
Faktorregel:
\(\displaystyle \int_{a}^{b} c \cdot f(x)\,dx = c \cdot \int_{a}^{b} f(x)\,dx\) mit \(c \in \mathbb R\)
Summenregel:
\[\int_{a}^{b} \left[f(x) \pm g(x) \right] dx = \int_{a}^{b}f(x)\,dx \pm \int_{a}^{b}g(x)\,dx\]
Vertauschungsregel:
\[\int_{a}^{b}f(x)\,dx = -\int_{b}^{a}f(x)\,dx\]
Zerlegung in Teilintervalle:
\(\displaystyle \int_{a}^{b}f(x)\,dx = \int_{a}^{c}f(x)\,dx + \int_{c}^{b}f(x)\,dx\) mit \(a \leq c \leq b\)
\[\begin{align*}A &= \int_{-1}^{3} d(x) dx \\[0.8em] &= \int_{-1}^{3} \left( -\sqrt{4 - x} - \sqrt{x + 2} + 6 \right) dx \\[0.8em] &=\left[ \frac{2}{3} \left( \sqrt{(4 - x)^{3}} - \sqrt{(x + 2)^{3}} \right) + 6x \right]_{-1}^{3} \\[0.8em] &= \frac{2}{3} \left( \sqrt{(4 - 3)^{3}} - \sqrt{(3 + 2)^{3}}\right) + 6 \cdot 3 - \left[ \frac{2}{3} \left( \sqrt{(4 - (-1))^{3}} - \sqrt{(-1 + 2)^{3}} \right) + 6 \cdot (-1) \right] \\[0.8em] &= \frac{2}{3}\left( 1 - 5\sqrt{5} \right) + 18 - \frac{2}{3}\left( 5\sqrt{5} - 1 \right) + 6 \\[0.8em] &= \frac{2}{3}\left( 2 - 10\sqrt{5} \right) + 24 \\[0.8em] &\approx 10{,}43 \end{align*}\]
f) Terme der Integralfunktion \(I(x)\) angeben, die die Maßzahl des Flächeninhalts \(A\) berechnen
Anmerkung:
Die zutreffenden Terme sind lediglich anzugeben. Jede Begründung kann entfallen.
Term (III) und Term (V) berechnen die Maßzahl des Flächeninhalts \(A\).
(III) \(I(3) - I(-1)\)
(V) \(\vert I(-1) \vert + I(3)\)
Begründung:
Die Treme (III) und (V) ergeben in der Integralschreibweise und unter Anwendung von Integrationsregeln jeweils das in Teilaufgabe e betrachtete bestimmte Integral zur Berechnung der Maßzahl des Flächeninhalts \(A\).
\[I(x) = \int_{0}^{x} d(t) dt\]
Berechnung bestimmter Integrale
\[\int_{a}^{b} f(x)\,dx = [F(x)]_{a}^{b} = F(b) - F(a)\]
Dabei ist \(F\) eine beliebige Stammfunktion zu \(f\).
(vgl. Merkhilfe)
Eigenschaften des bestimmten Integrals - Integrationsregeln
Identische Integrationsgrenzen:
\[\int_{a}^{a} f(x)\,dx = 0\]
Faktorregel:
\(\displaystyle \int_{a}^{b} c \cdot f(x)\,dx = c \cdot \int_{a}^{b} f(x)\,dx\) mit \(c \in \mathbb R\)
Summenregel:
\[\int_{a}^{b} \left[f(x) \pm g(x) \right] dx = \int_{a}^{b}f(x)\,dx \pm \int_{a}^{b}g(x)\,dx\]
Vertauschungsregel:
\[\int_{a}^{b}f(x)\,dx = -\int_{b}^{a}f(x)\,dx\]
Zerlegung in Teilintervalle:
\(\displaystyle \int_{a}^{b}f(x)\,dx = \int_{a}^{c}f(x)\,dx + \int_{c}^{b}f(x)\,dx\) mit \(a \leq c \leq b\)
\[\begin{align*}I(3) - I(-1) &= \int_{0}^{3} d(t) dt - \int_{0}^{-1} d(t) dt &&| \; \text{Vertauschungsregel anwenden} \\[0.8em] &= \int_{0}^{3} d(t) dt - \left( -\int_{-1}^{0} d(t) dt \right) \\[0.8em] &= \int_{-1}^{0} d(t) dt + \int_{0}^{3} d(t) dt &&| \; \text{Teilintervalle zusammenführen} \\[0.8em] &= \int_{-1}^{3} d(t) dt \\[0.8em] &= D(3) - D(-1) \end{align*}\]
\[\begin{align*} \vert I(-1) \vert + I(3) &= \left| \int_{0}^{-1} d(t) dt \right| + \int_{0}^{3} d(t) dt &&| \; \text{Vertauschungsregel anwenden} \\[0.8em] &= \left| -\int_{-1}^{0} d(t) dt \right| + \int_{0}^{3} d(t) dt \\[0.8em] &= \int_{-1}^{0} d(t) dt + \int_{0}^{3} d(t) dt &&| \; \text{Teilintervalle zusammenführen} \\[0.8em] &= \int_{-1}^{3} d(t) dt \\[0.8em] &= D(3) - D(-1) \end{align*}\]
Also berechnen die Terme (III) und (V) die Maßzahl des Flächeninhalts \(A\) (vgl. Teilaufgabe e), wobei \(D\) eine Stammfunktion von \(d\) ist.


