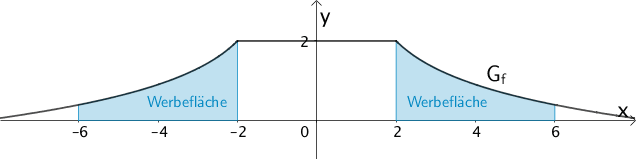
Die vordere Seitenfläche des Hinderniselements wird in Teilbereichen der Auf- und Abfahrt als Werbefläche verwendet (vgl. Abbildung 1). Im Modell handelt es sich um zwei Flächenstücke, nämlich um die Fläche zwischen \(G_{f}\) und der \(x\)-Achse im Bereich \(2 \leq x \leq 6\) sowie die dazu symmetrische Fläche im II-Quadranten. Berechnen Sie unter Verwendung der in Aufgabe 1d angegebenen Stammfunktion \(F\), wie viele Quadratmeter als Werbefläche zur Verfügung stehen.
(3 BE)
Lösung zu Teilaufgabe 2e
\[f(x) = 2 - \ln{(x - 1)}; \; D_{f} = ]1;+\infty[\]
\(F(x) = 3x - (x - 1) \cdot \ln{(x - 1)}; \; D_{F} = \; ]1;+\infty[\) (vgl. Teilaufgabe 1d)
Die insgesamt zur Verfügung stehende Werbefläche \(A\) errechnet sich aufgrund der beiden zur \(y\)-Achse symmetrischen Flächenstücke wie folgt:
Berechnung bestimmter Integrale
\[\int_{a}^{b} f(x)\,dx = [F(x)]_{a}^{b} = F(b) - F(a)\]
Dabei ist \(F\) eine beliebige Stammfunktion zu \(f\).
(vgl. Merkhilfe)
Eigenschaften des bestimmten Integrals - Integrationsregeln
Identische Integrationsgrenzen:
\[\int_{a}^{a} f(x)\,dx = 0\]
Faktorregel:
\(\displaystyle \int_{a}^{b} c \cdot f(x)\,dx = c \cdot \int_{a}^{b} f(x)\,dx\) mit \(c \in \mathbb R\)
Summenregel:
\[\int_{a}^{b} \left[f(x) \pm g(x) \right] dx = \int_{a}^{b}f(x)\,dx \pm \int_{a}^{b}g(x)\,dx\]
Vertauschungsregel:
\[\int_{a}^{b}f(x)\,dx = -\int_{b}^{a}f(x)\,dx\]
Zerlegung in Teilintervalle:
\(\displaystyle \int_{a}^{b}f(x)\,dx = \int_{a}^{c}f(x)\,dx + \int_{c}^{b}f(x)\,dx\) mit \(a \leq c \leq b\)
\[\begin{align*} A &= 2 \cdot \int_{2}^{6} f(x) dx \\[0.8em] &= 2 \cdot [F(x)]_{2}^{6} \\[0.8em] &= 2 \cdot [3x - (x - 1) \cdot \ln{(x - 1)}]_{2}^{6} \\[0.8em] &= 2 \cdot \left[ 3 \cdot 6 - (6 - 1) \cdot \ln{(6 - 1)} - \left( 3 \cdot 2 - (2 - 1) \cdot \ln{(2 - 1)} \right) \right] \\[0.8em] &= 2 \cdot \big[ 18 - 5\ln{5} - 6 + \underbrace{\ln{1}}_{0} \big] \\[0.8em] &= 2 \cdot (12 - 5\ln{5}) \\[0.8em] &= 24 - 10\ln{5} \\[0.8em] &\approx 7{,}91 \end{align*}\]
Als Werbefläche stehen insgesamt etwa 8 Quadratmeter zur Verfügung.


