Betrachtet wird die in \(]-3;+\infty[\) definierte Integralfunktion \(\displaystyle J \colon x \mapsto \int_{-2}^x f(t) dt\).
Begründen Sie, dass die in \(]-3;+\infty[\) definierte Funktion \(F \colon x \mapsto \frac{1}{2}x^2 -3x + 5 \cdot \ln{(x+3)}\) für \(x > -3\) eine Stammfunktion von \(f\) ist. Zeigen Sie damit, dass \(\lim \limits_{x\,\to\,-3} J(x) = -\infty\) gilt, und deuten Sie diese Aussage geometrisch.
(6 BE)
Lösung zu Teilaufgabe 1f
\[J(x) = \int_{-2}^x f(t)dt; \; D_J=\; ]-3;+\infty[\]
Nachweis, dass \(F\) eine Stammfunktion von \(f\) ist
Es ist zu zeigen, dass \(F'(x) = f(x)\) gilt (vgl. Angabe Aufgabe 1). Hierfür wird u. a. die Ableitung der natürlichen Logarithmusfunktion und die Kettenregel benötigt.
Stammfunktion
Eine differenzierbare Funktion \(F\) heißt eine Stammfunktion der Funktion \(f\), wenn für alle \(x \in D_f\) gilt:
\(F'(x) = f(x)\)
\[F(x) = \frac{1}{2}x^2 -3x + 5 \cdot \textcolor{#0087c1}{\ln{(\textcolor{#cc071e}{x+3})}}; \; D_F = \; ]-3;+\infty[\]
Ableitungen der Grundfunktionen
\[c' = 0 \enspace (c \in \mathbb R)\]
\[\left( x^r \right)' = r \cdot x^{r - 1} \enspace (r \in \mathbb R)\]
\[\left( \sqrt{x} \right)' = \frac{1}{2\sqrt{x}}\]
\[\left( \sin{x} \right)' = \cos{x}\]
\[\left( \cos{x} \right)' = -\sin{x}\]
\[\left( \ln{x} \right)' = \frac{1}{x}\]
\[\left( \log_{a}{x}\right)' = \frac{1}{x \cdot \ln{a}}\]
\[\left( e^x \right)' = e^x\]
\[\left(a^x \right)' = a^x \cdot \ln{a}\]
vgl. Merkhilfe
Faktorregel
\[\begin{align*}f(x) &= a \cdot \textcolor{#0087c1}{u(x)} \\[0.8em] f'(x) &= a \cdot \textcolor{#0087c1}{u'(x)}\end{align*}\]
Summenregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(x)} + \textcolor{#cc071e}{v(x)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(x)} + \textcolor{#cc071e}{v'(x)}\end{align*}\]
Produktregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v(x)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(x)} \cdot \textcolor{#cc071e}{v(x)} + \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v'(x)}\end{align*}\]
Quotientenregel
\[\begin{align*}f(x) &= \dfrac{\textcolor{#0087c1}{u(x)}}{\textcolor{#cc071e}{v(x)}} \\[0.8em] f'(x) &= \dfrac{\textcolor{#0087c1}{u'(x)} \cdot \textcolor{#cc071e}{v(x)} - \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v'(x)}}{[\textcolor{#cc071e}{v(x)}]^{2}}\end{align*}\]
Kettenregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(}\textcolor{#cc071e}{v(x)}\textcolor{#0087c1}{)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(}\textcolor{#cc071e}{v(x)}\textcolor{#0087c1}{)} \cdot \textcolor{#cc071e}{v'(x)}\end{align*}\]
vgl. Merkhilfe
\[\begin{align*}F'(x) &= \frac{1}{2} \cdot 2x - 3 + 5 \cdot \textcolor{#0087c1}{\frac{1}{\textcolor{#cc071e}{x+3}}} \cdot \textcolor{#cc071e}{1} \\[0.8em] &= x-3+\frac{5}{x+3} \\[0.8em] &= f(x) \end{align*}\]
Somit ist die Funktion \(F \colon x \mapsto \frac{1}{2}x^2 -3x + 5 \cdot \ln{(x+3)}\) für \(x > -3\) eine Stammfunktion von \(f\).
Nachweis, dass \(\lim \limits_{x\,\to\,-3} J(x) = -\infty\) gilt
Mithilfe der Stammfunktion \(F \colon x \mapsto \frac{1}{2}x^2 -3x + 5 \cdot \ln{(x+3)}\) von \(f\) lässt sich die Integralfunktion \(\displaystyle J(x) = \int_{-2}^x f(t)dt\) integralfrei darstellen.
Integralfreie Darstellung einer Integralfunktion
Es gilt:
\(\displaystyle I_{a}(x) = \int_{a}^{x} f(t)\, dt = F(x) - F(a)\), wobei \(F\) eine Stammfunktion von \(f\) ist.
\[\begin{align*}J(x) &= \int_{-2}^x f(t)dt = F(x) - F(-2) \\[0.8em] &= \frac{1}{2}x^2 -3x + 5 \cdot \ln{(x+3)} - \left( \frac{1}{2}(-2)^2 -3 \cdot (-2) + 5 \cdot \ln{(-2+3)} \right) \\[0.8em] &= \frac{1}{2}x^2 -3x + 5 \cdot \ln{(x+3)} - \big( 2 + 6 + 5 \cdot \underbrace{\ln{1}}_{0} \big) \\[0.8em] &= \frac{1}{2}x^2 -3x + 5 \cdot \ln{(x+3)} - 8\end{align*}\]
Grenzwertbetrachtung \(\lim \limits_{x\,\to\,-3} J(x)\) durchführen:
\[\lim \limits_{x\,\to\,-3} J(x) = \lim \limits_{x\,\to\,-3} \Big(\textcolor{#e9b509}{\underbrace{\frac{1}{2}x^2 -3x}_{\to\,13{,}5}} + 5 \cdot \textcolor{#0087c1}{\overbrace{\ln{(\textcolor{#cc071e}{\underbrace{x+3}_{\to\,0^+}})}}^{\to\,-\infty}} - 8\Big) = \textcolor{#0087c1}{-\infty}\]
Oder etwas kürzer formuliert:
\[\begin{align*}\lim \limits_{x\,\to\,-3} J(x) &= \lim \limits_{x\,\to\,-3} \left( F(x) - F(-2)\right) \\[0.8em] &= \lim \limits_{x\,\to\,-3} \Big(\textcolor{#e9b509}{\underbrace{\frac{1}{2}x^2 -3x}_{\to\,13{,}5}} + 5 \cdot \textcolor{#0087c1}{\overbrace{\ln{(\textcolor{#cc071e}{\underbrace{x+3}_{\to\,0^+}})}}^{\to\,-\infty}} - F(-2)\Big) \\[0.8em] &= \textcolor{#0087c1}{-\infty}\end{align*}\]
Der exakte Funktionswert \(F(-2)\) ist wegen \(\lim \limits_{x\,\to\,-3} \textcolor{#0087c1}{\ln{(\textcolor{#cc071e}{\underbrace{x+3}_{\to\,0^+}})}} = \textcolor{#0087c1}{-\infty}\) für die Grenzwertbetrachtung nicht von Bedeutung.
Geometrische Bedeutung des Grenzwerts \(\lim \limits_{x\,\to\,-3} J(x) = -\infty\)
\[J(x) = \int_{-2}^x f(t)dt; \; D_J=\; ]-3;+\infty[\]
Das ins Unendliche reichende Flächenstück, das \(G\), die \(x\)-Achse und die Gerade mit der Gleichung \(x = -3\) (senkrechte Asymptote, vgl. Teilaufgabe 1a) im II. Quadranten begrenzen, hat keinen endlichen Flächeninhalt.
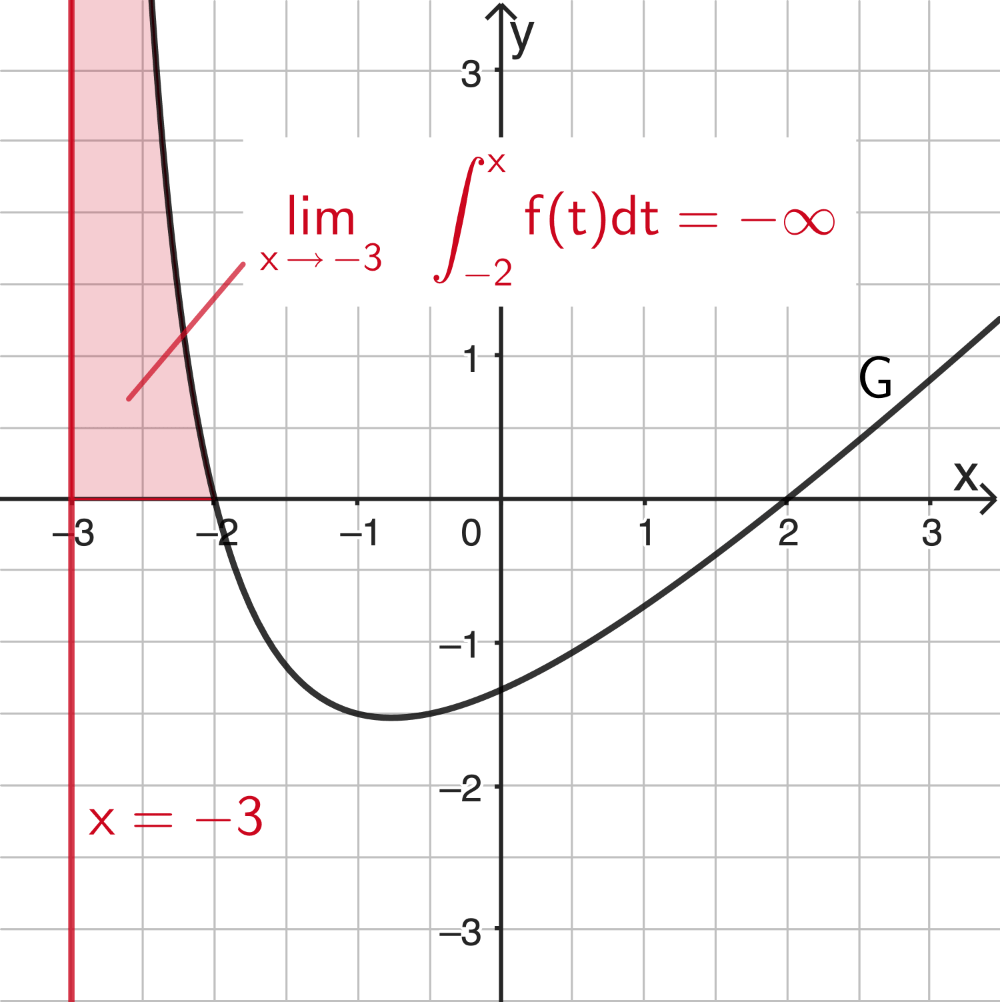ergänzende Skizze
Anmerkung
Zwar liegt das Flächenstück oberhalb der \(x\)-Achse, da aber mit \(x \to -3\) „nach links" integriert wird (obere Integrationsgrenze kleiner als untere), zählt der Inhalt negativ. Daher \(\lim \limits_{x\,\to\,-3} J(x) = \boldsymbol{-\infty}\)
