Gegeben ist die in \(\mathbb R \backslash \{0\}\) definierte Funktion \(f \colon x \mapsto 1 - \dfrac{1}{x^{2}}\), die die Nullstellen \(x_{1} = -1\) und \(x_{2} = 1\) hat. Abbildung 1 zeigt den Graphen von f, der symmetrisch bezüglich der \(y\)-Achse ist. Weiterhin ist die Gerade \(g\) mit der Gleichung \(y = -3\) gegeben.
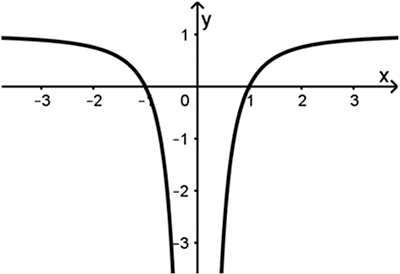 Abb. 1
Abb. 1
Zeigen Sie, dass einer der Punkte, in denen \(g\) den Graphen von \(f\) schneidet, die \(x\)-Koordinate \(\frac{1}{2}\) hat.
(1 BE)
Lösung zu Teilaufgabe 2a
\[f(x) = 1 - \frac{1}{x^{2}}; \; D_{f} = \mathbb R \backslash \{0\}\]
\(g \colon y = -3\) bzw. g(x) = -3
1. Möglichkeit: Gültigkeit der Gleichung \(f\big( \frac{1}{2} \big) = -3\) nachweisen
\[\begin{align*} f\big( \textstyle \frac{1}{2} \big) &= -3 \\[0.8em] 1 - \frac{1}{\left(\frac{1}{2}\right)^{2}} &= -3 \\[0.8em] 1 - \frac{1}{\frac{1}{4}} &= -3 \\[0.8em] 1 - 4 &= -3 \\[0.8em] -3 &= -3 && (\text{w}) \end{align*}\]
Also hat einer der Punkte, in denen \(g\) den Graphen von \(f\) schneidet, die \(x\)-Koordinate \(\frac{1}{2}\).
2. Möglichkeit: Schnittstellen von \(G_{f}\) und \(g\) berechnen
Für die Berechnung der Schnittstellen der Graphen zweier Funktionen werden die Funktionsterme gleichgesetzt.
\[\begin{align*} f(x) &= g(x) \\[0.8em] 1 - \frac{1}{x^{2}} &= -3 &&| \cdot x^{2} \\[0.8em] x^{2} - 1 &= -3x^{2} &&| + 3x^{2} + 1 \\[0.8em] 4x^{2} &= 1 &&| : 4 \\[0.8em] x^{2} &= \frac{1}{4} &&| \; \sqrt{\quad} \\[0.8em] x_{1,2} &= \pm \sqrt{\frac{1}{4}} \\[0.8em] &= \pm \frac{1}{2} \end{align*}\]
Somit hat einer der Punkte, in denen \(g\) den Graphen von \(f\) schneidet, die \(x\)-Koordinate \(\frac{1}{2}\).

