Gegeben ist die in \(\mathbb R\) definierte Funktion \(f \colon x \mapsto 2e^{-\frac{1}{8}x^2}\). Abbildung 1 zeigt den Graphen \(G_f\) von \(f\), der die \(x\)-Achse als waagrechte Asymptote besitzt.
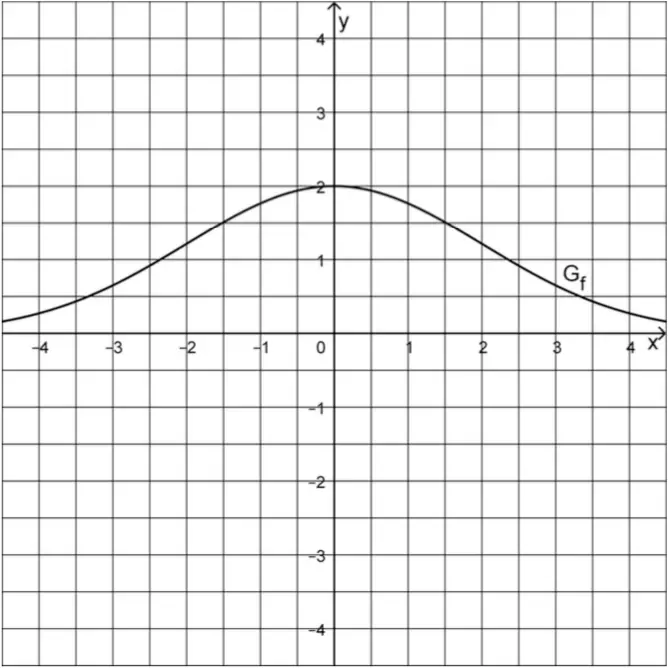Abb. 1
Berechnen Sie die Koordinaten des Schnittpunkts von \(G_f\) mit der \(y\)-Achse und weisen Sie rechnerisch nach, dass \(G_f\) symmetrisch bezüglich der \(y\)-Achse ist.
(2 BE)
Lösung zu Teilaufgabe 1a
\[f(x) = 2e^{-\frac{1}{8}x^2}; \; D_f = \mathbb R\]
Schnittpunkt von \(G_f\) mit der \(y\)-Achse
\(f(\textcolor{#e9b509}{0}) = 2e^{-\frac{1}{8} \cdot \textcolor{#e9b509}{0}^2} = 2e^0 = \textcolor{#0087c1}{2} \; \Rightarrow \; S_y(\textcolor{#e9b509}{0}|\textcolor{#0087c1}{2})\) (vgl. Abbildung 1)
Rechnerischer Nachweis, dass \(G_f\) symmetrisch bezüglich der \(y\)-Achse ist
Symmetrie von Funktionsgraphen bzgl. des Koordinatensystems
Der Graph einer Funktion \(f\) ist
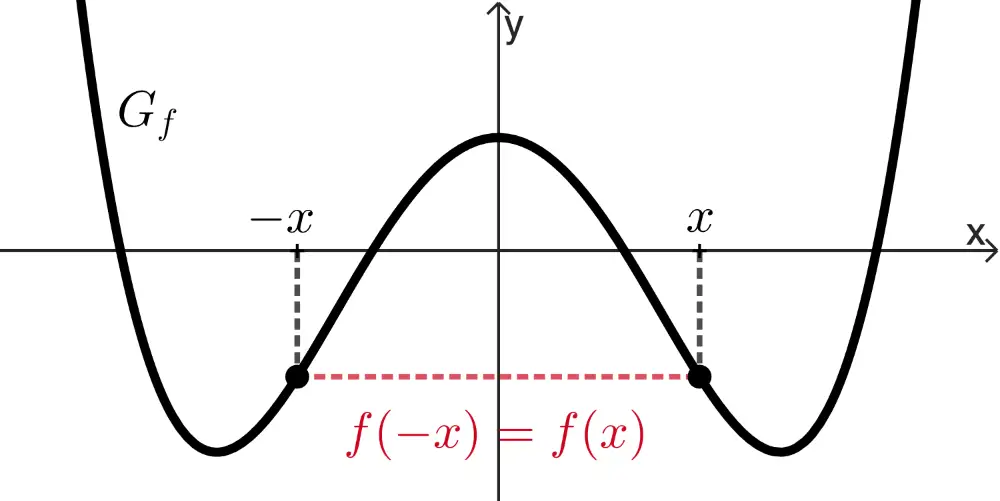
achsensymmetrisch bzgl. der \(\boldsymbol{y}\)-Achse,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = f(x)\).
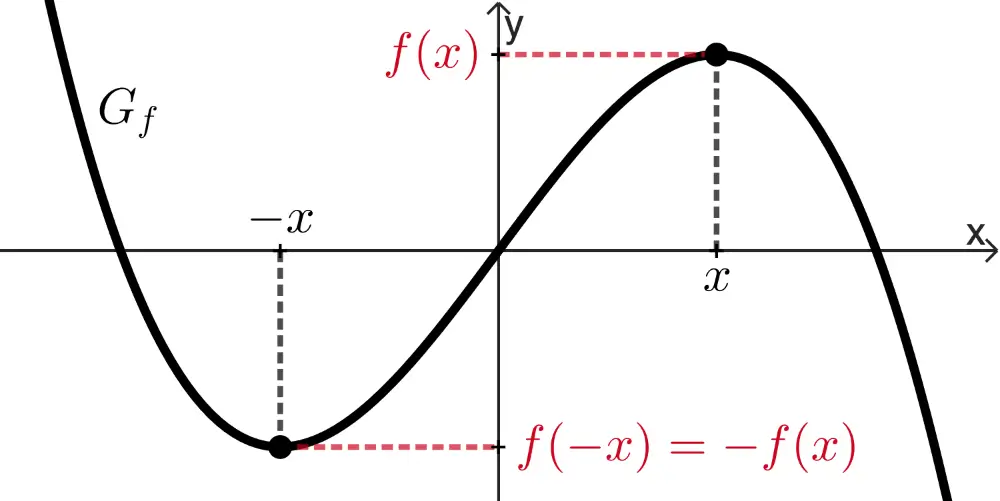
punktsymmetrisch bzgl. des Koordinatenursprungs,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = -f(x)\)
\[f(\textcolor{#cc071e}{-x}) = 2e^{-\frac{1}{8} \cdot \textcolor{#cc071e}{(-x)}^2} = 2e^{-\frac{1}{8}x^2} = f(x)\]
Mit \(f(\textcolor{#cc071e}{-x}) = f(x)\) ist \(G_{f}\) symmetrisch bezüglich der \(y\)-Achse.
