Berechnen Sie die Wahrscheinlichkeiten \(P(T)\) und \(P_T(S)\). Interpretieren Sie das Ergebnis für \(P_T(S)\) im Sachzusammenhang.
(zur Kontrolle: \(P(T) \approx 0{,}85\,\%\), \(P_T(S) < 0{,}1\))
(8 BE)
Lösung zu Teilaufgabe 2b
\(S\colon\enspace\)„Die Stoffwechselstörung liegt vor."
\(T\colon\enspace\)„Das Testergebnis ist positiv."
Analyse der Angabe (siehe Teilaufgabe 2a):
„Bei 0,074 % der neugeborenen Kinder liegt eine bestimmte Stoffwechselstörung vor."
\(\Longrightarrow \quad P(S) = 0{,}00074\)
„Liegt bei einem neugeborenen Kind die Stoffwechselstörung vor, so ist das Testergebnis mit einer Wahrscheinlichkeit von 99,5 % positiv."
Bedingte Wahrscheinlichkeit
Die Wahrscheinlichkeit für das Eintreten des Ereignisses \(B\) unter der Voraussetzung oder der Bedingung, dass das Ereignis \(A\) bereits eingetreten ist, heißt bedingte Wahrscheinlichkeit von \(\boldsymbol{B}\) unter der Bedingung \(\boldsymbol{A}\) und wird durch die Schreibweise \(P_{A}(B)\) gekennzeichnet.
Es gilt: \(P_{A}(B) = \dfrac{P(A \cap B)}{P(A)} \quad (P(A) \neq 0)\)
(vgl. Merkhilfe)
\(\Longrightarrow \quad P_S(T) = 0{,}995\)
„Liegt bei einem neugeborenen Kind die Stoffwechselstörung nicht vor, so beträgt die Wahrscheinlichkeit dafür, dass das Testergebnis irrtümlich positiv ist, 0,78 %.
\(\Longrightarrow \quad P_{\overline{S}}(T) = 0{,}0078\)
Berechnung der Wahrscheinlichkeiten \(P(T)\) und \(P_T(S)\)
Berechnung der Wahrscheinlichkeit \(P(T)\):
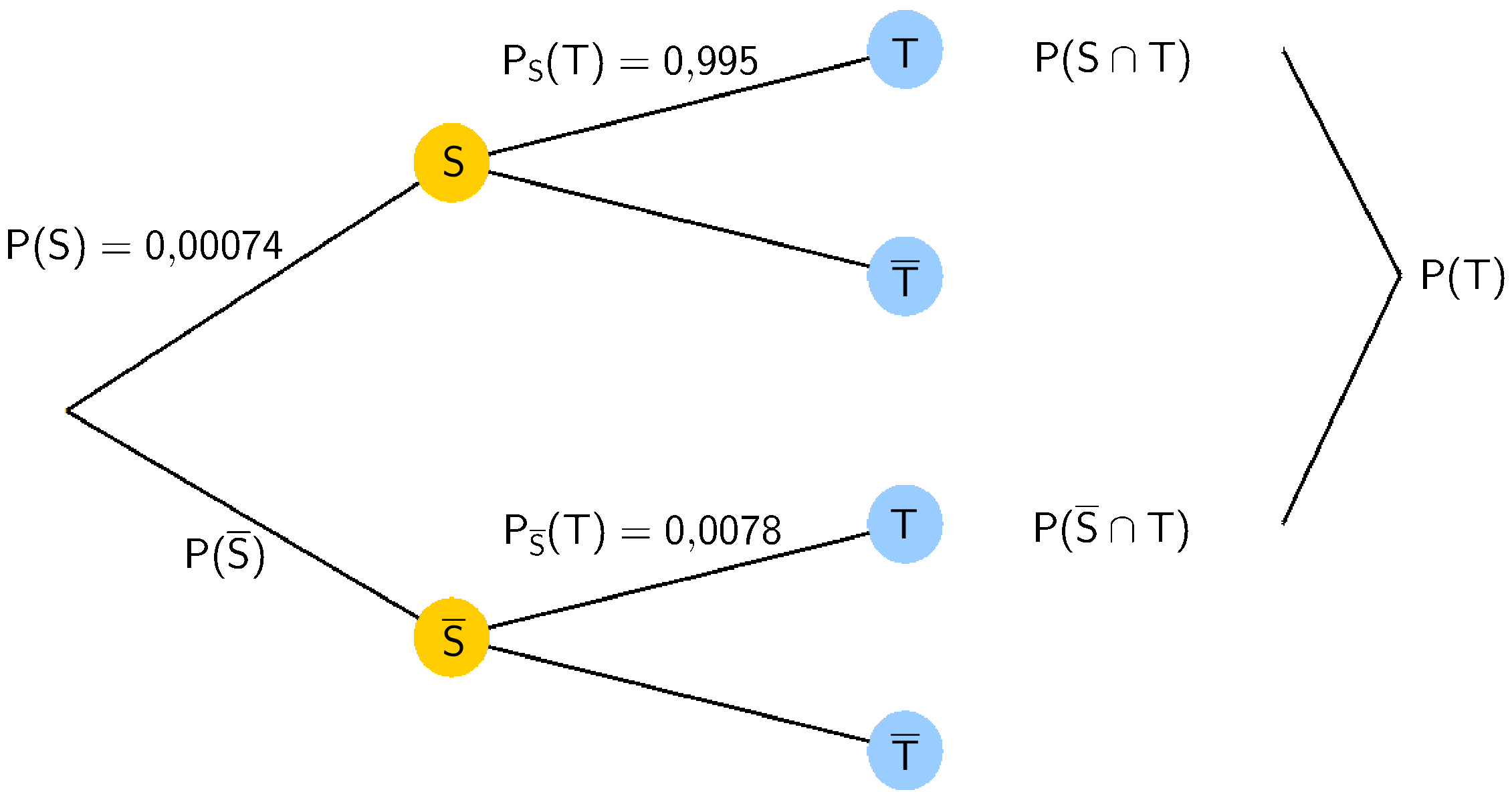
Baumdiagramm für die Ereignisse \(S\) und \(T\)
Pfadregeln
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu diesem Ereignis gehören.
Anwenden der Knotenregel:
\[\begin{align*} P(S) + P(\overline{S}) &= 1 & &| - P(S) \\[0.8em] P(\overline{S}) &= 1 - P(S) \\[0.8em] &= 1 - 0{,}00074 \\[0.8em] &= 0{,}99926 \end{align*}\]
Anwenden der 1. Pfadregel:
\[P(S \cap T) = P(S) \cdot P_S(T)\]
\[P(\overline{S} \cap T) = P(\overline{S}) \cdot P_{\overline{S}}(T)\]
Anwenden der 2. Pfadregel:
\[\begin{align*}P(T) &= P(S \cap T) + P(\overline{S} \cap T) \\[0.8em] &= P(S) \cdot P_S(T) + P(\overline{S}) \cdot P_{\overline{S}}(T) \\[0.8em] &= 0{,}00074 \cdot 0{,}995 + 0{,}99926 \cdot 0{,}0078 \\[0.8em] &\approx 0{,}00853 \\[0.8em] &\approx 0{,}85\,\%\end{align*}\]
Berechnung der Wahrscheinlichkeit \(P_T(S)\):
Bedingte Wahrscheinlichkeit
Die Wahrscheinlichkeit für das Eintreten des Ereignisses \(B\) unter der Voraussetzung oder der Bedingung, dass das Ereignis \(A\) bereits eingetreten ist, heißt bedingte Wahrscheinlichkeit von \(\boldsymbol{B}\) unter der Bedingung \(\boldsymbol{A}\) und wird durch die Schreibweise \(P_{A}(B)\) gekennzeichnet.
Es gilt: \(P_{A}(B) = \dfrac{P(A \cap B)}{P(A)} \quad (P(A) \neq 0)\)
(vgl. Merkhilfe)
\[\begin{align*} P_T(S) &= \frac{P(T \cap S)}{P(T)} \\[0.8em] &= \frac{P(S \cap T)}{P(T)} \\[0.8em] &= \frac{P(S) \cdot P_S(T)}{P(S) \cdot P_S(T) + P(\overline{S}) \cdot P_{\overline{S}}(T)} \\[0.8em] &= \frac{0{,}00074 \cdot 0{,}995}{0{,}00074 \cdot 0{,}995 + 0{,}99926 \cdot 0{,}0078} \\[0.8em] &\approx 0{,}0863 \\[0.8em] &= 8{,}63\,\% \end{align*}\]
Interpretation des Ergebnisses für \(P_T(S)\) im Sachzusammenhang
Die bedingte Wahrscheinlichkeit \(P_T(S)\) ist die Wahrscheinlichkeit dafür, dass ein zufällig ausgewähltes neugeborenes Kind, bei dem das Testegebnis positiv ist, tatsächlich eine bestimmte Stoffwechselstörung hat.
Diese Wahrscheinlichkeit ist mit 8,63 % sehr niedrig. Ein positives Testergebnis liefert somit keine verlässliche Aussage darüber, ob eine Stoffwechselstörung vorliegt.


