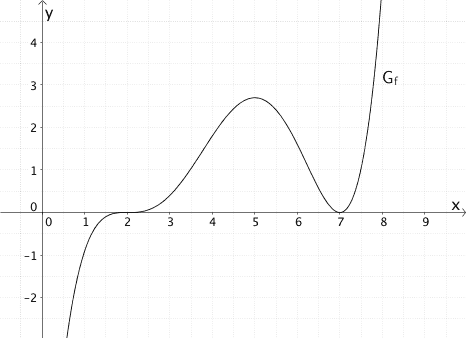
Die Abbildung zeigt den Graphen \(G_{f}\) einer Funktion \(f\). Die Ableitungsfunktion von \(f\) wird mit \(f'(x)\) bezeichnet, eine Stammfunktion von \(f\) wird mit \(F(x)\) bezeichnet.
Entscheiden Sie jeweils, ob die nachfolgenden Aussagen richtig oder falsch sind und begründen Sie Ihre Entscheidung.
a) \(f'(x)\) hat genau zwei Nullstellen.
b) \(f'(x) < 0\) für \(5{,}5 < x < 6{,}5\)
c) \(f'(6) > f'(7)\)
d) \(f'(4) \approx f'(6)\)
e) Der Graph von \(F(x)\) hat an der Stelle \(x = 6\) in etwa die Steigung \(-1\).
f) Der Graph von \(F(x)\) hat an der Stelle \(x = 7\) einen Terrassenpunkt.
a) \(f'(x)\) hat genau zwei Nullstellen.
Die Aussage ist falsch.
Begründung:
Anwendung der Differetialrechnung:
Steigung \(m_{T}\) einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\,(\,x_0\,|\,f(x_0)\,)\)
\[m_{T} = f'(x_0)\]
(vgl. Merkhilfe)
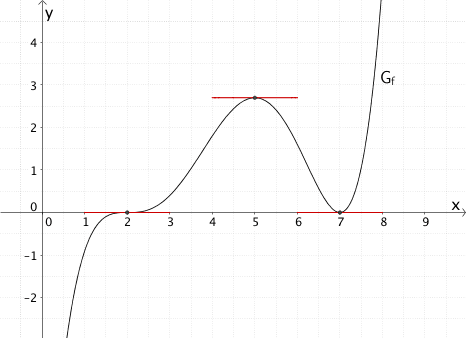
Der Graph der Funktion \(f\) besitzt drei waagrechte Tangenten, deren Steigung gleich Null ist. Da die Ableitungsfunktion \(f'\) die Steigung einer Tangente an den Graphen der Funktion \(f\) beschreibt, hat \(f'(x)\) drei Nullstellen.
b) \(f'(x) < 0\) für \(5{,}5 < x < 6{,}5\)
Die Aussage ist richtig.
Begründung:
Anwendung der Differetialrechnung:
Monotoniekriterium
\(\textcolor{#cc071e}{f'(x) < 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) fällt streng monoton in \(I\)
\(\textcolor{#0087c1}{f'(x) > 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
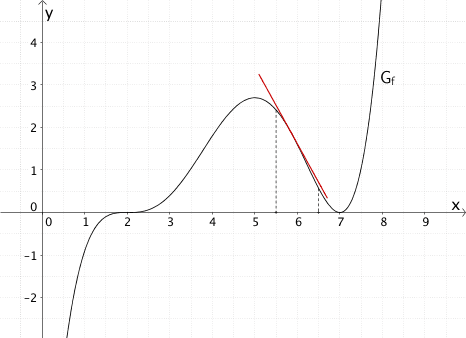
Der Graph der Funktion \(f\) ist für \(5{,}5 < x < 6{,}5\) streng monoton fallend. Folglich gilt nach dem Monotoniekriterium: \(f'(x) < 0\) für \(5{,}5 < x < 6{,}5\).
c) \(f'(6) > f'(7)\)
Die Aussage ist falsch.
Begründung:
Anwendung der Differetialrechnung:
Monotoniekriterium
\(\textcolor{#cc071e}{f'(x) < 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) fällt streng monoton in \(I\)
\(\textcolor{#0087c1}{f'(x) > 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
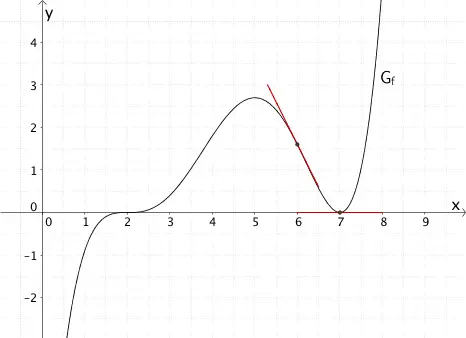
Die Ableitungsfunktion \(f'\) beschreibt die Steigung einer Tangente an den Graphen der Funktion \(f\).
Folglich gilt:
\[\left. \begin{align*} &f'(6) < 0 \\[0.8em] &f'(7) = 0 \end{align*} \right\} \enspace \Rightarrow \enspace f'(6) < f'(7)\]
d) \(f'(4) \approx f'(6)\)
Die Aussage ist falsch.
Begründung:
Anwendung der Differetialrechnung:
Monotoniekriterium
\(\textcolor{#cc071e}{f'(x) < 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) fällt streng monoton in \(I\)
\(\textcolor{#0087c1}{f'(x) > 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
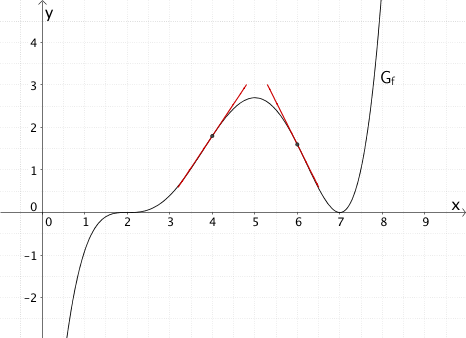
Die Ableitungsfunktion \(f'\) beschreibt die Steigung einer Tangente an den Graphen der Funktion \(f\).
Folglich gilt:
\[\left. \begin{align*} &f'(4) > 0 \\[0.8em] &f'(6) < 0 \end{align*} \right\} \enspace \Rightarrow \enspace f'(4) > f'(6)\]
e) Der Graph von \(F(x)\) hat an der Stelle \(x = 6\) in etwa die Steigung \(-1\).
Die Aussage ist falsch.
Begründung:
Stammfunktion
Eine differenzierbare Funktion \(F(x)\) heißt eine Stammfunktion von \(f(x)\), wenn
\(F'(x) = f(x)\) mit \(D_{F} = D_{f}\)
gilt.
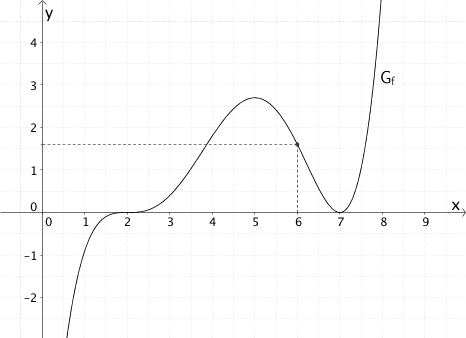
Gemäß der Definition einer Stammfunktion gilt \(F'(6) = f(6) \approx 1{.}6\).
Die Funktion \(F'(x) = f(x)\) beschreibt die Steigung einer Tangente an den Graphen einer Stammfunktion \(F\). Folglich hat der Graph von \(F\) an der Stelle \(x = 6\) die Steigung \(f(6) \approx 1{,}6\).
f) Der Graph von \(F(x)\) hat an der Stelle \(x = 7\) einen Terrassenpunkt.
Die Aussage ist richtig.
Begründung:
Stammfunktion
Eine differenzierbare Funktion \(F(x)\) heißt eine Stammfunktion von \(f(x)\), wenn
\(F'(x) = f(x)\) mit \(D_{F} = D_{f}\)
gilt.
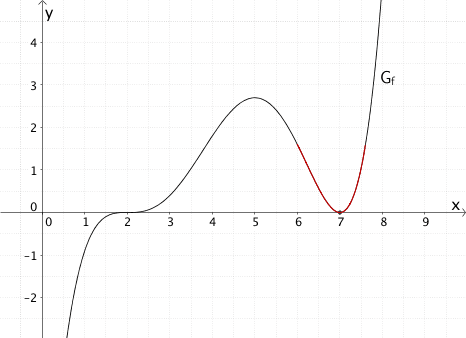
Der Graph der Funktion \(f\) hat an der Stelle \(x = 7\) eine doppelte Nullstelle ohne Vorzeichenwechsel.
Gemäß der Definition einer Stammfunktion gilt \(F'(x) = f(x)\). Folglich hat der Graph der Funktion \(F\) mit \(F'(7) = f(7) = 0\) eine waagrechte Tangente an der Stelle \(x = 7\) und ist in deren Umgebung mit \(f(x) > 0 \enspace \Rightarrow \enspace F'(x) > 0\) streng monoton steigend.
\[\left. \begin{align*} &F'(x) > 0 \; \text{für} \; x < 7 \\[0.8em] &F'(7) = 0 \\[0.8em] &F'(x) > 0 \, \text{für} \; x > 7 \end{align*} \right\} \enspace \Rightarrow \enspace \text{Terrassenpunkt an der Stelle}\; x = 7\]

