Abbildung 2 zeigt die Wahrscheinlichkeitsverteilung einer binomialverteilten Zufallsgröße \(Y\) mit den Parametern \(n = 3\) und \(p = \frac{2}{3}\). Zeigen Sie rechnerisch, dass \(Y\) den gleichen Erwartungswert wie die Zufallsgröße \(X\), aber eine größere Varianz als \(X\) besitzt.
Erläutern Sie, woran man durch Vergleich der Abbildungen 1 und 2 erkennen kann, dass \(Var(Y) > Var(X)\) gilt.
(4 BE)
Lösung zu Teilaufgabe 3c
Erwartungswert und Varianz der binomialverteilten Zufallsgröße \(Y\)
\[n = 3\,; \quad p = \frac{2}{3}\]
Erwartungswert der binomialverteilten Zufallsgröße \(Y\):
Erwartungswert \(\boldsymbol{\mu}\) einer binomialverteilten Zufallsgröße \(\boldsymbol{X}\)
\(\mu = E(X) = n \cdot p\) (vgl. Merkhilfe)
Wobei \(n\) die Länge der Bernoullikette und \(p\) die Trefferwahrscheinlichkeit für das Eintreten des betrachteten Ereignisses ist.
\[\mu = E(Y) = n \cdot p = 3 \cdot \frac{2}{3} = 2\]
Varianz der binomilaverteilten Zufallsgröße \(Y\):
Varianz \(Var(X)\) einer binomialverteilten Zufallsgröße \(X\):
\(Var(X) = n \cdot p \cdot (1 - p)\) (vgl. Merkhilfe)
Wobei \(n\) die Länge der Bernoulli-Kette und \(p\) die Trefferwahrscheinlichkeit für das Eintreten des betrachteten Ereignisses ist.
\[Var(Y) = n \cdot p \cdot (1 - p) = 3 \cdot \frac{2}{3} \cdot \left(1 - \frac{2}{3} \right) = \frac{2}{3}\]
Erläuterung, dass \(Var(Y) > Var(X)\) gilt, durch Vergleich der Abb. 1 und 2
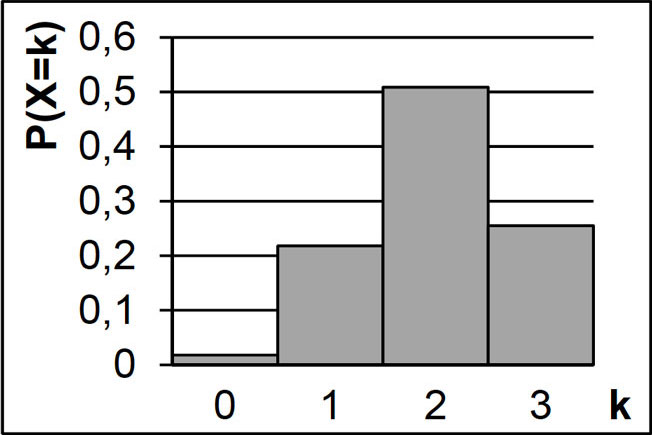 Abb. 1
Abb. 1
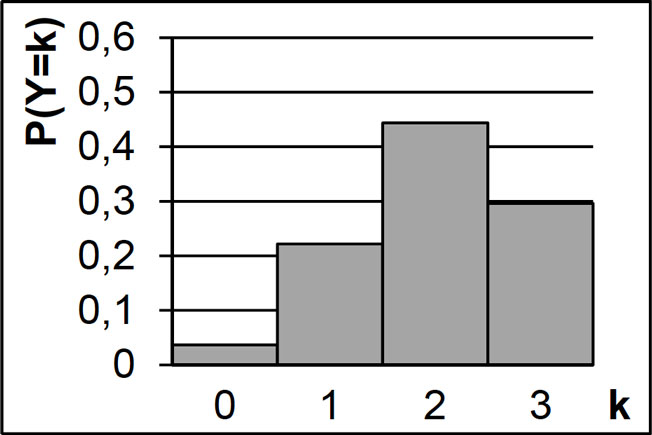 Abb. 2
Abb. 2
Die Varianz ist ein Maß dafür, wie stark die zu erwartenden Werte um den Erwartungswert streuen. Je größer die Wahrscheinlichkeit dafür ist, dass eine Zufallsgröße den Erwartungswert (bzw. einen dem Erwartungswert direkt benachbarten Wert) annimt, und je kleiner die Wahrscheinlichkeit dafür ist, dass eine Zufallsgröße einen dem Erwartungswert entfernten Wert annimt, desto weniger streuen die Werte einer Zufallsgröße.
Die Ungleichung \(Var(Y) > Var(X)\) sagt aus, dass die Zufallsgröße \(Y\) stärker um ihren Erwartungswert streut als die Zufallsgröße \(X\). Beide Zufallsgrößen besitzen denselben Erwartungswert \(\mu = 2\) (siehe auch Teiaufgabe 3b).
Vergleich der Wahrscheinlichkeiten \(P(X = \mu)\) und \(P(Y = \mu)\):
Aus Teilaufgabe 1a ist bekannt:
\[P(X = \mu) = P(X = 2) = \frac{28}{55} \approx 0{,}51\]
Aus Abb. 2 entnimmt man im Rahmen der Ablesegenauigkeit:
\[P(Y = \mu) = P(Y = 2) \approx 0{,}44\]
\[\Longrightarrow \quad P(X = \mu) > P(Y = \mu)\]
Vergleich der übrigen Wahrscheinlichkeiten:
Da der Erwartungswert \(\mu = 2\) der Zufallsgrößen \(X\) und \(Y\) ein Wert der Zufallsgrößen selbst ist (was im Allgemeinen nicht der Fall ist), geben die Wahrscheinlichkeiten aller übrigen Werte der Zufallsgößen weitere Auskunft über die Streuung der Zufallsgrößen.
Aus Teilaufgabe 1a ist bekannt:
\[P(X = 0) = \frac{1}{55} \approx 0{,}02\]
\[P(X = 1) = \frac{12}{55} \approx 0{,}22\]
\[P(X = 3) = \frac{14}{55} \approx 0{,}25\]
Aus Abb. 2 entnimmt man im Rahmen der Ablesegenauigkeit:
\[P(Y = 0) \approx 0{,}03\]
\[P(Y = 1) \approx 0{,}22\]
\[P(Y = 3) \approx 0{,}30\]
\[\begin{align*}\Longrightarrow \quad P(X = 0) &< P(Y = 0) \\[0.8em] \Longrightarrow \quad P(X = 1) &\approxeq P(Y = 1) \\[0.8em] \Longrightarrow \quad P(X = 3) &< P(Y = 3) \end{align*}\]
Schlussfolgerung:
Die Wahrscheinlichkeitsverteilung der Zufallsgröße \(X\) konzentriert sich mehr auf den Erwartungswert \(\mu\) als dies bei der Zufallsgröße \(Y\) der Fall ist. Demnach streut die Zufallsgröße \(Y\) stärker.
\[\Longrightarrow \quad Var(Y) > Var(X)\]


