Berechnen Sie das arithmetische Mittel der beiden in den Aufgaben 2b und 2c berechneten Näherungswerte. Skizzieren Sie den Graphen von \(F\) für \(0 \leq x \leq 3\) unter Berücksichtigung der bisherigen Ergebnisse in Abbildung 1
(4 BE)
Lösung zu Teilaufgabe 2d
Arithmetisches Mittel der beiden Näherungswerte für \(F(1)\)
Näherungswert aus Teilaufgabe 2b: \(F(1) \approx -0{,}5\)
Näherungswert aus Teilaufgabe 2c: \(F(1) \approx -\dfrac{2}{\pi}\)
Arithmetisches Mittel (Durchschnitt)
\[\overline{x} = \frac{x_1 + x_2 + ... + x_n}{n} = \frac{1}{n} \sum_{i\, =\, 1}^n \; x_i\]
Wobei \(x_i\) die zu berücksichtigenden Werte sind und \(n\) die Anzahl der Werte ist.
\[\frac{-0{,}5 + \left( -\frac{2}{\pi} \right)}{2} \approx -0{,}57\]
Skizzieren des Graphen von \(F\) für \(0 \leq x \leq 3\) unter Berücksichtigung der bisherigen Ergebnisse
Bisherige Ergebnisse:
● \(x = 0\) ist Nullstelle von \(F\) (vgl. Teilaufgabe 2a).
● Im Intervall \([1;3]\) hat \(F\) eine weitere Nullstelle bei \(x \approx 2{,}3\) (vgl. Teilaufgabe 2a)
● Der Punkt \((-1|F(-1))\) ist Hochpunkt von \(G_{F}\) (vgl. Teilaufgabe 2a). Analog lässt sich schlussfolgern, dass der Punkt \((1|F(1))\) Tiefpunkt von \(G_{f}\) ist.
● \(F(1) \approx -0{,}57\) (vgl. oben)
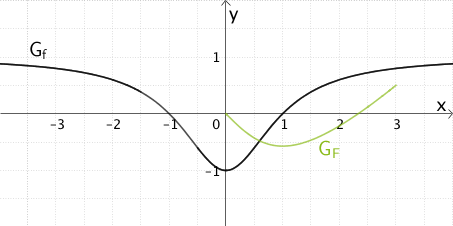
Graph der Integralfunktion \(\displaystyle F \colon x \mapsto \int_{0}^{x}f(t)dt\) im Bereich \(0 \leq x \leq 3\)
Ausführliche Erklärung (nicht verlangt)
In Teilaufgabe 2a wurde erklärt, weshalb der Punkt \((-1|F(-1))\) ein Hochpunkt von \(G_{F}\) ist. Analog dazu lässt sich begründen, weshalb der Punkt \((1|F(1))\) ein Tiefpunkt von \(G_{F}\) ist.
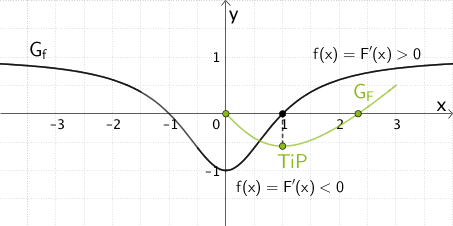
Abbildung 1 bzw. dem Funktionsterm \(f(x) = \dfrac{x^{2} - 1}{x^{2} + 1}\) ist zu entnehmen, dass \(x = 1\) eine einfache Nullstelle von \(f\) ist.
\[f(x) = 0 \enspace \Rightarrow \enspace x^{2} - 1 = 0 \enspace \Rightarrow \enspace x_{1,2} = \pm 1\]
Hauptsatz der Differential- und Integralrechnung (HDI)
Jede Integralfunktion \(\displaystyle I_{a} \colon x \mapsto \int_{a}^{x} f(t)\, dt\) einer stetigen Funktion \(f\) ist eine Stammfunktion von \(f\).
\[I_{a}(x) = \int_{a}^{x} f(t)\, dt \quad \Longrightarrow \quad I'_{a}(x) = f(x)\]
(vgl. Merkhilfe)
Nach dem Hauptsatz der Differential- und Integralrechnung ist die Integralfunktion \(F\) eine Stammfunktion von f und es gilt somit:
Stammfunktion
Eine differenzierbare Funktion \(F(x)\) heißt eine Stammfunktion von \(f(x)\), wenn
\(F'(x) = f(x)\) mit \(D_{F} = D_{f}\)
gilt.
\[f(11) = F'(1) = 0\]
Anwendung der Differetialrechnung:
Monotoniekriterium
\(\textcolor{#cc071e}{f'(x) < 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) fällt streng monoton in \(I\)
\(\textcolor{#0087c1}{f'(x) > 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
An der Nullstelle \(x = 1\) wechselt \(f(x) = F'(x)\) das Vorzeichen von \(-\) nach \(+\). Gemäß dem Monotoniekriterium wechselt demzufolge der Graph der Integralfunktion \(F\) an der Stelle \(x = 1\) das Monotonieverhalten von „streng monoton fallend" zu „streng monoton steigend". Also hat \(G_{F}\) an der Stelle \(x = 1\) den Tiefpunkt \(TiP(1|F(1))\).
Anwendung der Differentialrechnung:
Extrempunkte
Ist \(f'(x_{0}) = 0\) und wechselt \(f'\) an der Stelle \(x_{0}\) das Vorzeichen, so hat \(G_{f}\) an der Stelle \(x_{0}\) einen Extrempunkt.
(vgl. Merkhilfe)
\[\left. \begin{align*} &f(x) = F'(x) < 0 \enspace \text{für} \enspace x < 1 \\ &f(1) = F'(1) = 0 \\ &f(x) = F'(x) > 0 \enspace \text{für} \enspace x > 1 \end{align*} \right \} \enspace \Rightarrow \enspace \textcolor{#89ba17}{\text{Tiefpunkt} \; TiP\,(1|F(1))}\]

