Eine dritte Modellierung des Querschnitts der Tunnelwand, bei der ebenfalls die Bedingungen I und II erfüllt sind, verwendet die Funktion \(f \colon x \mapsto \sqrt{25 - x^{2}}\) mit dem Definitionsbereich \(D_{f} = [-5;5]\).
Begründen Sie, dass in diesem Modell jeder Punkt des Querschnitts der Tunnelwand von der Bodenmitte \(M\) den Abstand 5 m hat. Zeichnen Sie den Graphen von \(f\) in ein Koordinatensystem ein (Platzbedarf im Hinblick auf spätere Aufgaben: \(-5 \leq x \leq 9\), \(-1 \leq y \leq 13\)) und begründen Sie, dass bei dieser Modellierung auch Bedingung III erfüllt ist.
(5 BE)
Lösung zu Teilaufgabe 3a
Satz des Pythagoras anwenden, Funktionswert im Sachzusammenhang bewerten
\[f(x) = \sqrt{25 - x^{2}}; \; D_{f} = [-5;5]\]
Begründung, dass jeder Punkt des Querschnitts der Tunnelwand von der Bodenmitte \(M\) den Abstand 5 m hat
In Teilaufgabe 1b wurde der Abstand \(d(x)\) eines Graphenpunktes \(P(x|p(x))\) zum Ursprung des Koordinatensystems \(M\) mithilfe es Satzes des Pythagoras ermittelt bzw. bestätigt. Diese Anwendung lässt sich auf Graphenpunkte \(P(x|f(x))\) übertragen.
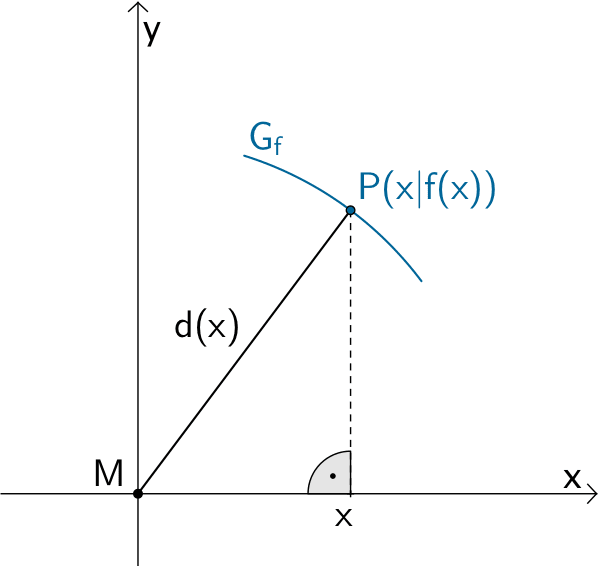
Der Abstand \(d(x)\) eines Graphenpunktes \(P(x|f(x))\) von der Bodenmitte \(M\) (Koordinatenursprung) kann mithilfe des Satzes des Pythagoras formuliert werden.
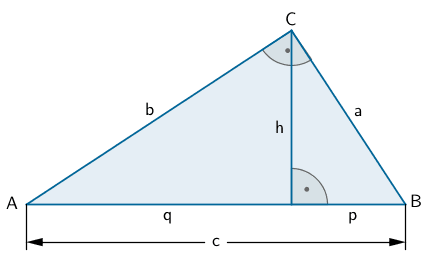
Satzgruppe des Pythagoras im rechtwinkligen Dreieck
Satz des Pythagoras
\[\hspace{5px}a^2 + b^2 = c^2\]
Höhensatz
\[h^2 = p \cdot q\]
Kathetensatz
\[a^2 = c \cdot p\,; \enspace b^2 = c \cdot q\]
\[f(x) = \sqrt{25 - x^{2}}; \; D_{f} = [-5;5]\]
\[\begin{align*}[d(x)]^{2} &= x^{2} + [f(x)]^{2} & &| \; \sqrt{\enspace} \enspace d(x) > 0 \\[0.8em] d(x) &= \sqrt{x^{2} + [f(x)]^{2}} \\[0.8em] &= \sqrt{x^{2} + \left( \sqrt{25 - x^{2}} \right)^{2}} \\[0.8em] &= \sqrt{x^{2} + 25 - x^{2}} \\[0.8em] &= \sqrt{25} \\[0.8em] &= 5 \end{align*}\]
\(\Longrightarrow \quad d(P(x|f(x));M) = 5\)
Folglich hat in diesem Modell jeder Punkt des Querschnitts der Tunnelwand von der Bodenmitte \(M\) den Abstand 5 m.
Anmerkung:
Der Abstand d(x) der Graphenpunkte \(P_{x}(x|f(x))\) vom Koordinatenursprung ist ein im Sachzusammenhang positiver Wert. Wegen \(d(x) > 0\) kann hier die Wurzel beidseitig der Gleichung „problemlos" (ohne Fallunterscheidung) gezogen werden. Das ist nicht selbstverständlich, denn allgemein gilt: \(\sqrt{a^{2}} = \vert a \vert; \; a \in \mathbb R\).
Einzeichnen von \(G_{f}\) in ein Koordinatensystem
Die Ortslinie aller Punkte \(P\), deren Abstand zu einem Punkt \(M\) mit \(d(P;M) = 5\) konstant ist, ist ein Kreis mit dem Mittelpunkt \(M\) und dem Radius \(r = d(P;M) = 5\). Da für \(x \in D_{f}\) stets \(f(x) > 0\) gilt, beschreibt der Graph der Funktion \(f\) einen Halbkreis mit dem Mittelpunkt \(M\) und dem Radius \(r = 5\), der oberhalb der \(x\)-Achse verläuft.
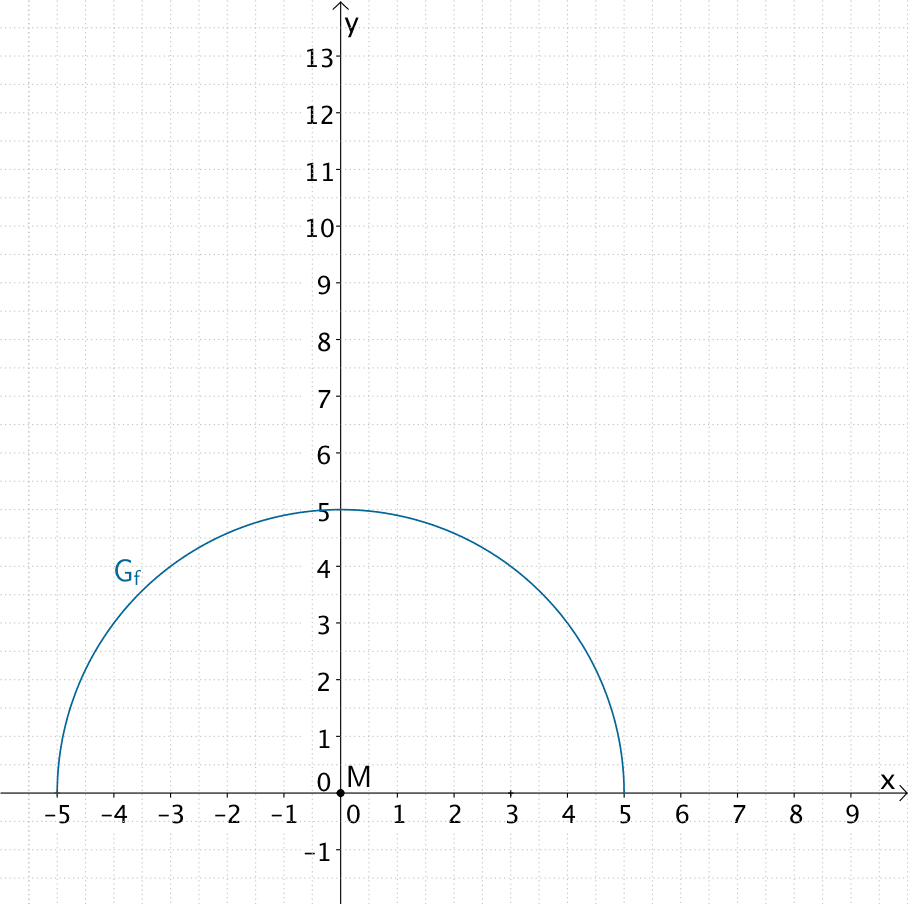
Graph der Funktion \(f \colon x \mapsto \sqrt{25 - x^{2}}\), Halbkreis mit Mittelpunkt \(M\) und Radius \(r = 5\)
Begründung, dass Bedingung III erfüllt ist
Bedingung III:
Der Tunnel ist auf einer Breite von mindestens 6 m mindestens 4 m hoch.
![Graph der Funktion \(f\) mit D = [-5;5], Punkte (-5|f(-5)) und (5|f(5)) Graph der Funktion \(f\) mit D = [-5;5], Punkte (-5|f(-5)) und (5|f(5))](/images/stories/B2016_PT_B_A_2/B2016_PT_B_A_2_3a_3.png)
Das Intervall \(x \in [-3;3]\) entspricht einer zum Mittelpunkt \(M\) des Tunnelbodens symmetrischen Breite von 6 m. Um zu bestätigen, dass Bedingung III bei einer Modellierung mit \(f\) erfüllt ist, berechnet man die Funktionswerte \(f(-3)\) und \(f(3)\).
Damit Bedingung III erfüllt ist, muss gelten:
\(f(x) \geq 4\) für \(x \in [-3;3]\)
Aufgrund der Achsensymmetrie des Graphen der Funktion \(f\) gilt \(f(-3) = f(3)\).
Nachweis der Achsensymmetrie zur \(y\)-Achse von \(G_{f}\):
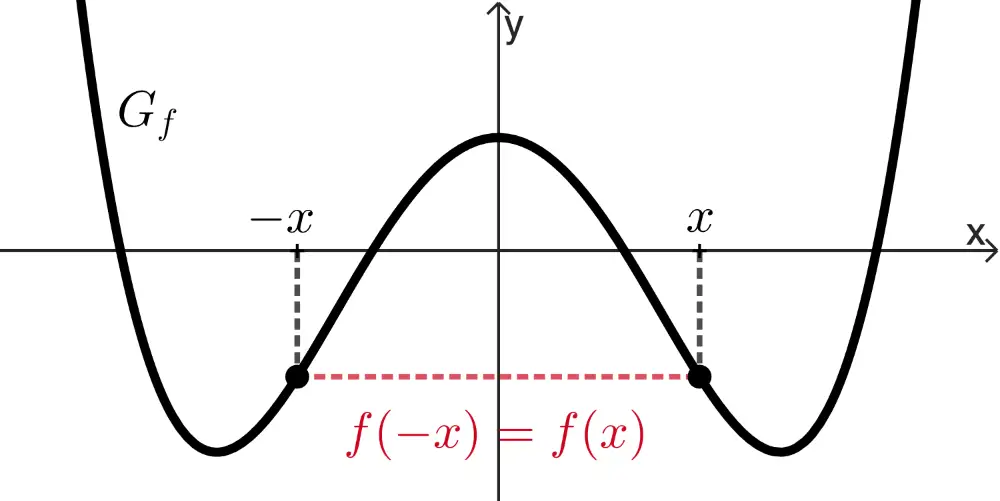
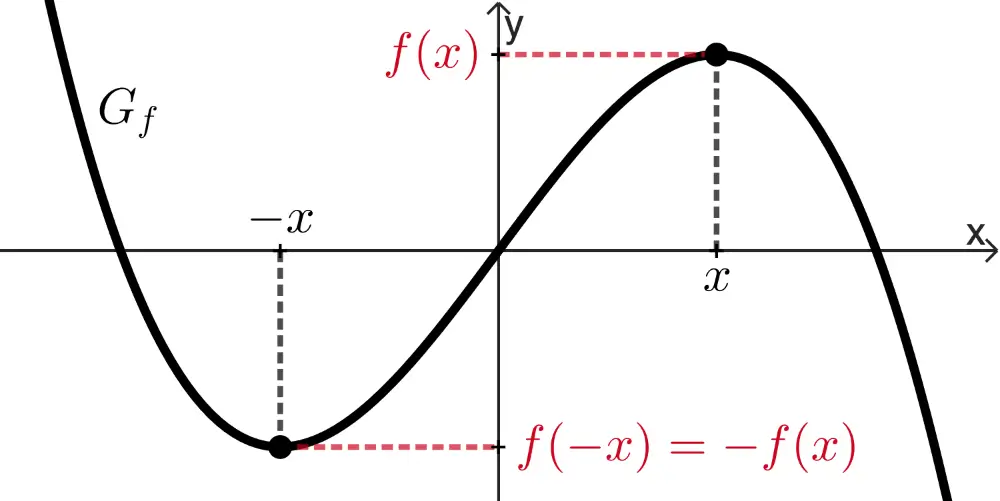
Symmetrie von Funktionsgraphen bzgl. des Koordinatensystems
Der Graph einer Funktion \(f\) ist
achsensymmetrisch bzgl. der \(\boldsymbol{y}\)-Achse,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = f(x)\).
punktsymmetrisch bzgl. des Koordinatenursprungs,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = -f(x)\)
\[f(x) = \sqrt{25 - x^{2}}; \; D_{f} = [-5;5]\]
\[f(-x) = \sqrt{25 - (-x)^{2}} = \sqrt{25 - x^{2}} = f(x)\]
Funktionswerte \(f(-3)\) und \(f(3)\) berechnen:
\[f(-3) = f(3) = \sqrt{25 - 3^{2}} = \sqrt{16} = 4\]
\(\Longrightarrow \quad f(x) \geq 4\) für \(x \in [-3;3]\)
\(\Longrightarrow \quad\)Bedingung III ist erfüllt.


