Gemeinsame Punkte einer Kurvenschar
Betrachtet wird die Kurvenschar \(G_{f_{k}}\) einer Funktionenschar \(f_{k}\). Gibt es gemeinsame Punkte, durch die alle Graphen der Kurvenschar verlaufen?
Wollte man beispielsweise die gemeinsamen Punkte der Graphen \(G_{f_{1}}\) der Scharfunktion \(f_{1}\) für \(k = 1\) und \(G_{f_{2}}\) der Scharfunktion \(f_{2}\) für \(k = 2\) berechnen, würde man die Lösungen der Gleichung \(f_{1}(x) = f_{2}(x)\) ermitteln.
Um die gemeinsamen Punkte der Kurvenschar \(G_{f_{k}}\) der Funktionenschar \(f_{k}\) zu bestimmen, ersetzt man den Parameter \(k\) zunächst einmal durch einen Parameter \(m\) und einmal durch einen Parameter \(n\). Anschließend erfolgt die Bestimmung der Schnittstellen von \(f_{m}\) und \(f_{n}\) für den Fall \(m \neq n\).
Es ergibt sich folgender Ansatz:
\[f_{m}(x) = f_{n}(x) \quad (m \neq n)\]
Schließlich werden noch die \(y\)-Koordinaten der gemeinsamen Punkte errechnet und die Punkte angegeben.
Beispielaufgabe
Gegeben sei die in \(\mathbb R\) definierte Funktionenschar \(f_{k} \colon x \mapsto \frac{1}{10}\left[ x^{3} + 2kx^{2} + (6k - 2)x \right]\) mit \(k \in \mathbb R\).
Bestimmen Sie die gemeinsamen Punkte der Kurvenschar \(G_{f_{k}}\).
\[f_{k}(x) = \frac{1}{10}\left[ x^{3} + 2kx^{2} + (6k - 2)x \right]; \; D_{f_{k}} = \mathbb R, \; k \in \mathbb R\]
Parameter \(k\) durch Parameter \(m\) bzw. Parameter \(n\) ersetzen:
\[f_{m}(x) = \frac{1}{10}\left[ x^{3} + 2mx^{2} + (6m - 2)x \right]\]
\[f_{n}(x) = \frac{1}{10}\left[ x^{3} + 2nx^{2} + (6n - 2)x \right]\]
Schnittstellen von \(f_{m}\) und \(f_{n}\) für \(m \neq n\) berechnen:
\[\begin{align*} f_{m}(x) &= f_{n}(x) \\[0.8em] \frac{1}{10}\left[ x^{3} + 2mx^{2} + (6m - 2)x \right] &= \frac{1}{10}\left[ x^{3} + 2nx^{2} + (6n - 2)x \right] & &| \cdot 10 \\[0.8em] x^{3} + 2mx^{2} + (6m - 2)x &= x^{3} + 2nx^{2} + (6n - 2)x & &| - x^{3} \\[0.8em] 2mx^{2} + (6m - 2)x &= 2nx^{2} + (6n - 2)x \\[0.8em] x\left( 2mx + 6m - 2 \right) &= x\left( 2nx + 6n - 2 \right) & &| : x \enspace (x \neq 0) \\[0.8em] 2mx + 6m - 2 &= 2nx + 6n - 2 & &| - 2nx - 6m + 2 \\[0.8em] 2mx - 2nx &= 6n - 6m \\[0.8em] 2x(m - n) &= -6(m - n) & &| : (m - n) \enspace (m \neq n) \\[0.8em] 2x &= -6 & &| : 2 \\[0.8em] x &= -3 \end{align*}\]
\[\begin{align*}f_{k}(-3) &= \frac{1}{10}\left[ (-3)^{3} + 2k \cdot (-3)^{2} + (6k - 2) \cdot (-3) \right] \\[0.8em] &= \frac{1}{10}(-27 + 18k - 18k + 6) \\[0.8em] &= -2{,}1 \end{align*}\]
Der Punkt \((-3|-2{,}1)\) ist gemeinsamer Punkt der Kurvenschar \(G_{f_{k}}\) der Funktionenschar \(f_{k}\).
Bei der Umformung wurde \(x\) unter der Bedingung \(x \neq 0\) gekürzt. Der Fall \(x = 0\) muss gesondert betrachtet werden:
\[f_{k}(x) = \frac{1}{10}\left[ x^{3} + 2kx^{2} + (6k - 2)x \right]\]
\[f_{k}(0) = \frac{1}{10}\left[ 0^{3} + 2k \cdot 0^{2} + (6k - 2) \cdot 0 \right] = 0\]
Der Ursprung \((0|0)\) ist gemeinsamer Punkt der Kurvenschar \(G_{f_{k}}\) der Funktionenschar \(f_{k}\).
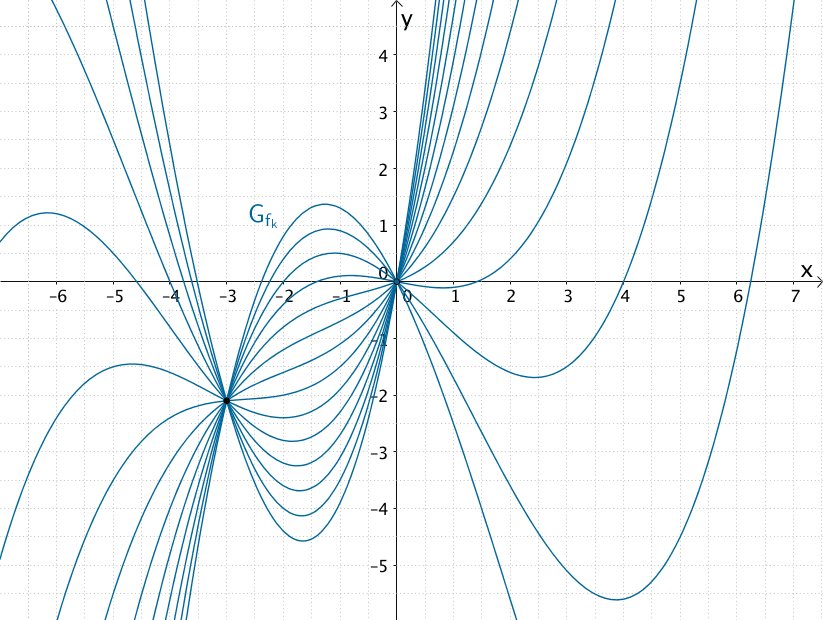
Gemeinsame Punkte \((0|0)\) und \((-3|-2{,}1)\) der Kurvenschar \(G_{f_{k}}\) der in \(\mathbb R\) definierten Funktionenschar \(f_{k} \colon x \mapsto \frac{1}{10}\left[ x^{3} + 2kx^{2} + (6k - 2)x \right]\) mit \(k \in \mathbb R\)


