Ein Hubschrauber überfliegt das Grundstück entlang einer Linie, die im Modell durch die Gerade
\[g\colon \enspace \overrightarrow X = \begin {pmatrix} -20 \\ 40 \\ 40 \end {pmatrix} + \lambda \cdot \begin {pmatrix} 4 \\ 5 \\ -3 \end {pmatrix}\,, \enspace \lambda \in \mathbb R \;,\]
beschrieben wird.
Weisen Sie nach, dass der Hubschrauber mit einem konstanten Abstand von 20 m zum Hang fliegt.
(3 BE)
Lösung zu Teilaufgabe d
Eine Fluglinie mit konstantem Abstand zum Hang bedeutet, dass der Hubschrauber parallel zum Hang fliegt. Demnach muss gelten: \(g \parallel E\).
Gegenseitige Lage der Geraden \(g\) und der Ebene \(E\)
Lagebeziehung von Gerade und Ebene
| \(g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u}; \; \lambda \in \mathbb R \enspace\) und \(\enspace E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{B}) = 0\) | |||
| \(\overrightarrow{u} \circ \overrightarrow{n}_{E} = 0 \enspace \Longleftrightarrow \enspace \overrightarrow{u} \perp \overrightarrow{n}_{E}\) | \(\overrightarrow{u} \circ \overrightarrow{n}_{E} \neq 0\) | ||
|
\(A \in E\) \(\Longrightarrow \enspace g \subset E\) \(g\) liegt in der Ebene \(E\)
|
\(A \notin E\) \(\Longrightarrow \quad g \parallel E\) \(g\) verläuft (echt) parallel zur Ebene \(E\) (ggf. Abstand berechnen).
|
\(\Longrightarrow \enspace\)\(g\) schneidet die Ebene \(E\) im Schnittpunkt \(S\) unter dem Schnittwinkel \(\alpha\) (ggf. Schnittpunkt und/oder Schnitwinkel berechnen). |
|
Anwenden des Skalarprodukts:
Anwendung des Skalarprodukts:
Orthogonale (zueinander senkrechte) Vektoren (vgl. Merkhilfe)
\[\overrightarrow{a} \perp \overrightarrow{b} \; \Leftrightarrow \; \overrightarrow{a} \circ \overrightarrow{b} \quad (\overrightarrow{a} \neq \overrightarrow{0},\; \overrightarrow{b} \neq \overrightarrow{0})\]
Die Gerade \(g\) verläuft dann parallel zur Ebene \(E\), wenn das Skalarprodukt aus dem Richtungsvektor \(\overrightarrow u\) der Geraden \(g\) und dem Normalenvektor \(\overrightarrow {n}_E\) der Ebene \(E\) gleich Null ist, also wenn gilt: \(\overrightarrow u \perp \overrightarrow {n}_E\).
\[g \colon \enspace \overrightarrow X = \begin {pmatrix} -20 \\ 40 \\ 40 \end {pmatrix} + \lambda \cdot \begin {pmatrix} 4 \\ 5 \\ -3 \end {pmatrix} \quad \Longrightarrow \quad \overrightarrow u = \begin {pmatrix} 4 \\ 5 \\ -3 \end {pmatrix}\]
\[E \colon \enspace \begin {pmatrix} 3 \\ 0 \\ 4 \end {pmatrix} \circ \left[ \overrightarrow X - \begin {pmatrix} 0 \\ 60 \\ 0 \end {pmatrix} \right] = 0 \quad \Longrightarrow \quad \overrightarrow {n}_E = \begin {pmatrix} 3 \\ 0 \\ 4 \end {pmatrix}\]
\[\overrightarrow u \circ \overrightarrow {n}_E = \begin {pmatrix} 4 \\ 5 \\ -3 \end {pmatrix} \circ \begin {pmatrix} 3 \\ 0 \\ 4 \end {pmatrix} = 4 \cdot 3 + 5 \cdot 0 + (-3) \cdot 4 = 12 - 12 = 0\]
\[\Longrightarrow \quad \overrightarrow u \perp \overrightarrow {n}_E \quad \Longrightarrow \quad g \parallel E\]
Abstand \(d\,(g; E)\) zwischen der Geraden \(g\) und der Ebene \(E\)
Die Abstandsbestimmung einer Geraden, die parallel zu einer Ebene verläuft, lässt sich auf die Berechnung des Abstands eines Punktes zu einer Ebene zurückführen.
\(g \colon \enspace \overrightarrow X = \begin {pmatrix} -20 \\ 40 \\ 40 \end {pmatrix} + \lambda \cdot \begin {pmatrix} 4 \\ 5 \\ -3 \end {pmatrix} \quad \Longrightarrow \quad\) \(G\,(-20|40|40)\) ist Aufpunkt der Geraden \(g\).
\[\Longrightarrow \quad d\,(g; E) = d\,(G; E)\]
Abstand eines Punktes von einer Ebene
Für den Abstand \(d(P;E)\) eines Punktes \(P(p_{1}|p_{2}|p_{3})\) zu einer in der Hesseschen Normalenform (HNF) vorliegenden Ebene \(E\) gilt:
Vektordarstellung
\[E \colon \overrightarrow{n}^{0}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0 \enspace (\text{HNF})\]
\[d(P;E) = \left| \overrightarrow{n}^{0}_{E} \circ (\overrightarrow{P} - \overrightarrow{A}) \right|\]
Koordinatendarstellung
\[E \colon \frac{n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0}}{\sqrt{n_{1}^{2} + n_{2}^{2} + n_{3}^{2}}} = 0 \enspace (\text{HNF})\]
\[d(P;E) = \left| \frac{n_{1}p_{1} + n_{2}p_{2} + n_{3}p_{3} + n_{0}}{\sqrt{n_{1}^{2} + n_{2}^{2} + n_{3}^{2}}} \right|\]
Dabei ist \(\overrightarrow{n}^{0}_{E} = \dfrac{\overrightarrow{n}_{E}}{\vert \overrightarrow{n}_{E} \vert}\) der Einheitsvektor des Normalenvektors \(\overrightarrow{n}_{E}\) der Ebene \(E\).
\(E \colon \enspace 3x_1 + 4x_3 = 0\) (siehe Teilaufgabe 1a)
\[\overrightarrow {n}_E = \begin {pmatrix} 3 \\ 0 \\ 4 \end {pmatrix}\]
Betrag des Normalenvektors der Ebene \(E\):
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\left| \overrightarrow {n}_E \right| = \left| \begin {pmatrix} 3 \\ 0 \\ 4 \end {pmatrix} \right| = \sqrt{3^2 + 0^2 + 4^2} = 5 \]
\[E^{HNF} \colon \enspace \frac{3x_1 + 4x_3}{5} = 0\]
Abstand \(d\,(G; E)\) berechnen:
\[G\,(-20|40|40)\]
\[d\,(G; E) = \left| \frac{3g_1 + 4g_3}{5} \right| = \left| \frac{3 \cdot (-20) + 4 \cdot 40}{5} \right| = 20 \]
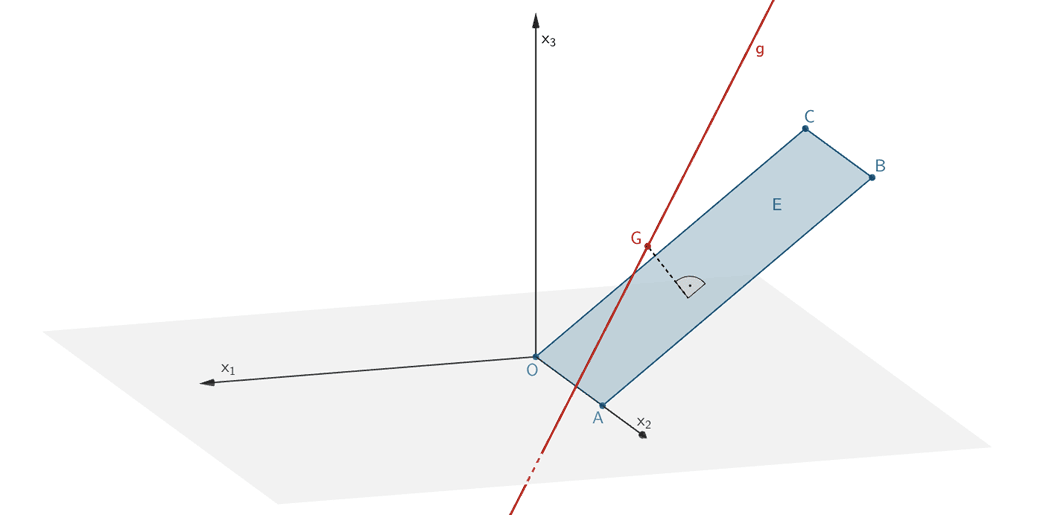
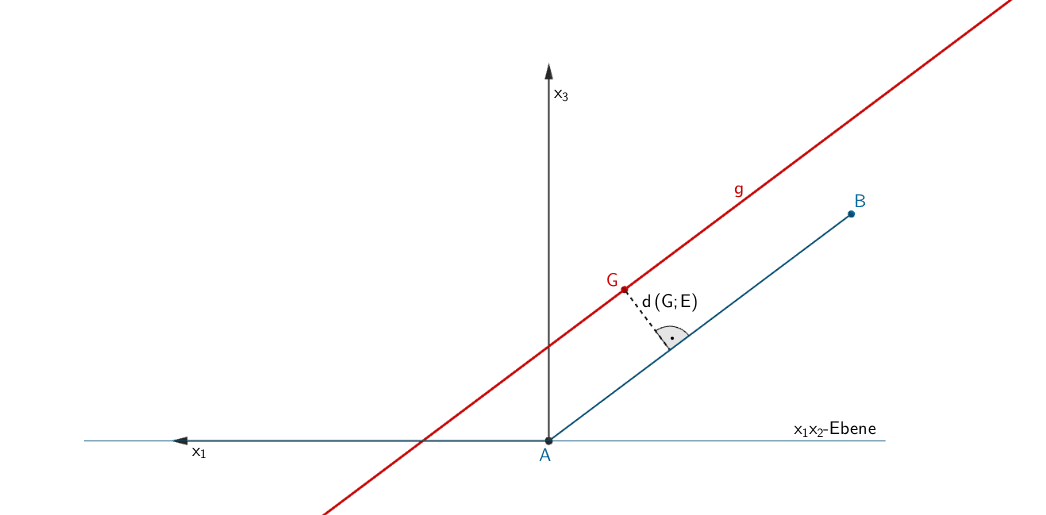
Der Hubschrauber fliegt entlang der Geraden \(g\) mit dem konstanten Abstand \(d(G;E) = 20 \; \text{m}\) parallel zum Hang (Ebene \(E\)).


