Das Trapez \(ABCD\) liegt in der Ebene \(H\).
Bestimmen Sie eine Gleichung von \(H\) in Koordinatenform.
(zur Kontrolle: \(H \colon 8x_1 + 15x_3 - 136 = 0\))
(3 BE)
Lösung zu Teilaufgabe c

Beispielsweise liefert das Vektorprodukt \(\textcolor{#e9b509}{\overrightarrow{DA}} \times \textcolor{#0087c1}{\overrightarrow{DC}}\) einen Normalenvektor \(\overrightarrow{n}\) der Ebene \(H\).
Ebenengleichung in Normalenform
Jede Ebene lässt sich durch eine Gleichung in Normalenform beschreiben. Ist \(\textcolor{#0087c1}{A}\) ein beliebiger Aufpunkt der Ebene \(\textcolor{#0087c1}{E}\) und \(\textcolor{#e9b509}{\overrightarrow{n}}\) ein Normalenvektor von \(E\), so erfüllt jeder Punkt \(X\) der Ebene \(E\) folgende Gleichungen:

Normalenform in Vektordarstellung
\[E \colon \textcolor{#e9b509}{\overrightarrow{n}} \circ (\overrightarrow{OX} - \textcolor{#0087c1}{\overrightarrow{OA}}) = 0\]
Normalenform in Koordinatendarstellung
\[E \colon \textcolor{#e9b509}{n_{1}}x_{1} + \textcolor{#e9b509}{n_{2}}x_{2} + \textcolor{#e9b509}{n_{3}}x_{3} + k = 0\]
mit \(k = -(\overrightarrow{n} \circ \overrightarrow{OA}) = - n_{1}a_{1} - n_{2}a_{2} - n_{3}a_{3}\)
\(n_{1}\), \(n_{2}\) und \(n_{3}\): Koordinaten eines Normalenvektors \(\overrightarrow{n}\)
Sind zwei linear unabhängige Richtungsvektoren \(\textcolor{#cc071e}{\overrightarrow{u}}\) und \(\textcolor{#cc071e}{\overrightarrow{v}}\) einer Ebene \(E\) bekannt, liefert das Vektorprodukt \(\textcolor{#cc071e}{\overrightarrow{u}} \times \textcolor{#cc071e}{\overrightarrow{v}}\) einen Normalenvektor \(\textcolor{#e9b509}{\overrightarrow{n}}\) der Ebene \(E\).
\(\textcolor{#e9b509}{\overrightarrow{DA}} = \textcolor{#e9b509}{\begin{pmatrix} 15 \\ 0 \\ -8 \end{pmatrix}}\), \(\textcolor{#0087c1}{\overrightarrow{DC}} = \textcolor{#0087c1}{\begin{pmatrix} 0 \\ 14 \\ 0 \end{pmatrix}}\) (vgl. Teilaufgabe a)
Vektorprodukt (Kreuzprodukt)
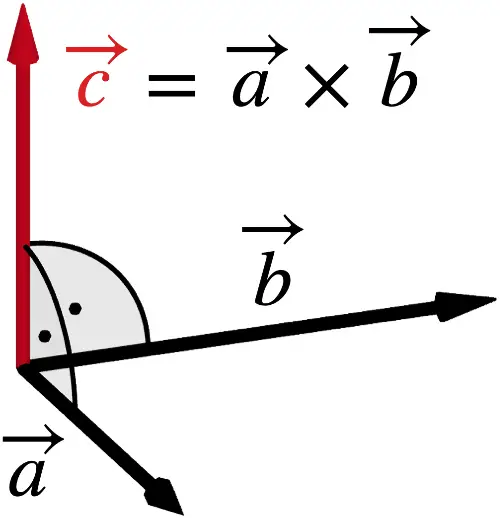
Das Vektorprodukt \(\overrightarrow{a} \times \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\neq \overrightarrow{0}\) und \(\overrightarrow{b} \neq \overrightarrow{0}\), die nicht parallel zueinander sind, erzeugt einen neuen Vektor \(\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b}\), der zu beiden Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) orthogonal (senkrecht) ist.
\[\textcolor{#cc071e}{\overrightarrow{c}} = \overrightarrow{a} \times \overrightarrow{b} \, \Rightarrow \begin{cases}\textcolor{#cc071e}{\overrightarrow{c}} \circ \overrightarrow{a} = 0\; \Leftrightarrow \;\textcolor{#cc071e}{\overrightarrow{c}} \perp \overrightarrow{a} \\\textcolor{#cc071e}{\overrightarrow{c}} \circ \overrightarrow{b} = 0\; \Leftrightarrow \;\textcolor{#cc071e}{\overrightarrow{c}} \perp \overrightarrow{b}\end{cases} \quad (\overrightarrow{a} \neq \overrightarrow{0},\, \overrightarrow{b} \neq \overrightarrow{0},\, \overrightarrow{a} \neq k \cdot \overrightarrow{b}\;\text{mit} \;k \in \mathbb R \backslash \{0\})\]
Es gilt: \(\overrightarrow{a} \times \overrightarrow{b} = \begin {pmatrix} a_1 \\ a_2 \\ a_3 \end {pmatrix} \times \begin {pmatrix} b_1 \\ b_2 \\ b_3 \end {pmatrix} = \begin {pmatrix} a_2 \cdot b_3 - a_3 \cdot b_2 \\ a_3 \cdot b_1 - a_1 \cdot b_3 \\ a_1 \cdot b_2 - a_2 \cdot b_1 \end {pmatrix}\)
\(\overrightarrow{a} \times \overrightarrow{b} = -\left(\overrightarrow{b} \times \overrightarrow{a}\right)\)
(Das Kommutativgesetz gilt nicht.)
Die Rechte-Hand-Regel beschreibt die gegenseitige Lage der Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\textcolor{#cc071e}{\overrightarrow{c}} = \overrightarrow{a} \times \overrightarrow{b}\) im Raum. Weist \(\overrightarrow{a}\) in Richtung des Daumens und \(\overrightarrow{b}\) in Richtung des Zeigefingers, so weist der Mittelfinger in Richtung von \(\textcolor{#cc071e}{\overrightarrow{c}} = \overrightarrow{a} \times \overrightarrow{b}\).

\[\begin{align*}\textcolor{#e9b509}{\overrightarrow{DA}} \times \textcolor{#0087c1}{\overrightarrow{DC}} &= \textcolor{#e9b509}{\begin{pmatrix} 15 \\ 0 \\ -8 \end{pmatrix}} \times \textcolor{#0087c1}{\begin{pmatrix} 0 \\ 14 \\ 0 \end{pmatrix}} \\[0.8em] &= \begin{pmatrix} 0& \cdot & 0 & - & (-8) & \cdot & 14 \\ -8 & \cdot & 0 & - & 15 & \cdot & 0 \\ 15 & \cdot & 14 & - & 0 & \cdot & 0 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 112 \\ 0 \\ 210 \end{pmatrix} = 14 \cdot \begin{pmatrix} 8 \\ 0 \\ 15 \end{pmatrix} \end{align*}\]
Somit ist \(\overrightarrow{n} = \begin{pmatrix} 8 \\ 0 \\ 15 \end{pmatrix}\) ein Normalenvektor der Ebene \(H\).
Als Aufpunkt für die Gleichung der Ebenen \(H\) in Koordinatenform wird beispielsweise Punkt \(\textcolor{#cc071e}{D(2|-10|8)}\) gewählt.
Ansatz mit Vektordarstellung
\[\begin{align*}&H \colon \overrightarrow{n} \circ (\overrightarrow{OX} - \textcolor{#cc071e}{\overrightarrow{OD}}) = 0 \\[0.8em] &H \colon \begin{pmatrix} 8 \\ 0 \\ 15 \end{pmatrix} \circ \left[ \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} - \textcolor{#cc071e}{\begin{pmatrix} 2 \\ -10 \\ 8 \end{pmatrix}} \right] = 0 \\[0.8em] &H \colon 8 \cdot (x_1 - \textcolor{#cc071e}{2}) + 0 \cdot (x_2 - \textcolor{#cc071e}{(-10)}) + 15 \cdot (x_3 - \textcolor{#cc071e}{8}) \\[0.8em] &H \colon 8x_1 - 16 + 15x_3 - 120 = 0 \\[0.8em] &H \colon 8x_1 + 15x_3 -136 =0\end{align*}\]
Ansatz mit Koordinatendarstellung
\[\begin{align*} &H\colon n_1x_1 + n_2x_2 + n_3x_3 + k = 0 \\[0.8em] &H \colon 8x_1 + 15x_3 + k = 0 \\[0.8em] \textcolor{#cc071e}{D} \in \; &H \colon 8 \cdot \textcolor{#cc071e}{2} + 15 \cdot \textcolor{#cc071e}{8} + k = 0 \\[1.6em] &\Rightarrow 136 + k = 0 \; \Leftrightarrow \; k = -136 \\[1.6em] &H \colon 8x_1 + 15x_3 - 136 = 0\end{align*}\]
(Vgl. Mathematik Abiturskript Bayern G9 - 3 Geometrie, 3.3.3 Ebenengleichung in Normalenform)


