Abbildung 1 zeigt den Graphen \(G_{f}\) einer ganzrationalen Funktion \(f\) drittens Grades mit Definitionsmenge \(\mathbb R\). \(G_{f}\) schneidet die \(x\)-Achse bei \(x = 0\), \(x = 5\) und \(x = 10\) und verläuft durch den Punkt \((1|2)\).
Ermitteln Sie einen Funktionsterm von \(f\).
(zur Kontrolle: \(f(x) = \frac{1}{18} \cdot (x^{3} - 15x^{2} + 50x)\))
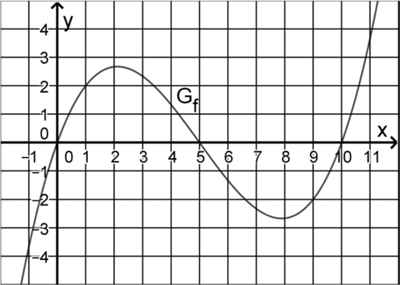Abb. 1
(4 BE)
Lösung zu Teilaufgabe 1a
Anhand der Nullstellen \(x_{1} = 0\), \(x_{2} = 5\) und \(x_{3} = 10\) (vgl. Abb. 1) lässt sich der Funktionsterm der ganzrationalen Funktion \(f\) in der vollständig faktorisierten Form \(f(x) = a\cdot (x - x_{1})(x - x_{2})(x - x_{3})\) angeben. Dabei ist \(a\) ein zunächst unbekannter Faktor, der eine Streckung von \(G_{f}\) in \(y\)-Richtung bewirkt und die Lage der Nullstellen nicht beeinflusst.
Strecken von Funktionsgraphen
Streckung in \(\textcolor{#0087c1}{x}\)-Richtung mit Streckungsfaktor \(\textcolor{#0087c1}{k}\,\):
\[h(x) = f\left(\textcolor{#0087c1}{\frac{1}{k}} \cdot x \right), \enspace k > 0\]
Streckung in \(\textcolor{#0087c1}{x}\)-Richtung mit Streckungsfaktor \(\textcolor{#0087c1}{\dfrac{1}{k}}\):
\[h(x) = f(\textcolor{#0087c1}{k} \cdot x), \enspace k > 0\]
Streckung in \(\textcolor{#cc071e}{y}\)-Richtung mit Streckungsfaktor \(\textcolor{#cc071e}{k}\,\):
\[g(x) = \textcolor{#cc071e}{k} \cdot f(x), \enspace k > 0\]
\[\begin{align*}f(x) &= a \cdot (x - 0)(x - 5)(x - 10) \\[0.8em] &= a \cdot x(x - 5)(x - 10) \end{align*}\]
Mit \(P(1|2) \in G_{f}\) ergibt sich \(a\):
\[\begin{align*} 2 &= a \cdot 1 \cdot (1 - 5)(1 - 10) \\[0.8em] 2 &= 36a &&| : 36 \\[0.8em] \frac{1}{18} &= a \end{align*}\]
\[\Longrightarrow \quad f(x) = \frac{1}{18} \cdot x(x - 5)(x - 10)\]
{zen-hand-o-right}Anmerkungen{/zen-hand-o-right}
Durch Ausmultiplizieren erhält man das Kontrollergebnis der Aufgabenstellung. Dieser Schritt ist aber nicht zwingend notwendig, da lediglich ein Funktionsterm von \(f\) zu ermitteln ist.
\[\begin{align*} f(x) &= \frac{1}{18} \cdot x(x - 5)(x - 10) \\[0.8em] &= \frac{1}{18} \cdot x(x^{2} -15x +50) \\[0.8em] &= \frac{1}{18} \cdot (x^{3} - 15x^{2} + 50x) \end{align*}\]
Der Ansatz \(f(x) = ax^{3} + bx^{2} + cx + d\) ist grundsätzlich möglich, aber deutlich zeitaufwendiger und daher nicht empfehlenswert.
Die Koordinaten des Punktes \((0|0)\) eingesetzt, liefert \(d = 0\).
Die Koordinaten der Punkte \((5|0)\), \((10|0)\) und \(P(1|2)\) eingesetzt, liefert jeweils eine lineare Gleichung mit \(a\), \(b\) und \(c\), also insgesamt ein lineares Gleichungssystem mit drei Gleichungen für die zu bestimmenden Unbekannten \(a\), \(b\) und \(c\). Die Lösung des Gleichungssystems ist zeitaufwendig.
