Gegeben sind die Punkte \(A(-3|-1|4)\), \(B(0|6|5)\) und \(C(3|2|1)\).
a) Prüfen Sie, ob die drei Punkte \(A\), \(B\) und \(C\) auf einer Gerade liegen.
b) Eine Gleichung der Gerade \(AB\) in Parameterform ist gegeben mit \(AB \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{AB}; \; \lambda \in \mathbb R\). Beschreiben Sie ausgehend von dieser Geradengleichung die Strecke [AB].
a) Untersuchung, ob die drei Punkte \(A\), \(B\) und \(C\) auf einer Gerade liegen
Je zwei der drei Punkte \(A\), \(B\) und \(C\) legen einen Gerade fest. Eine Punktprobe des dritten Punktes untersucht, ob dieser ebenfalls auf der Gerade liegt.
Beispielsweise legen die Punkte \(A\) und \(B\) die Gerade \(AB\) fest. Mit Punkt \(A\) als Aufpunkt und dem Verbindungsvektor \(\overrightarrow{AB}\) als möglichen Richtungsvektor ergibt sich folgende Geradengleichung (vgl. Abiturskript - 2.2.1 Geradengleichung in Parameterform):
Gleichung einer Gerad / Strecke in Parameterform
Jede Gerade \(g\) kann durch eine Gleichung in der sogenannten Parameterform
\(g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u} \enspace\) mit dem Parameter \(\lambda \in \mathbb R\) beschrieben werden.
Dabei ist \(\overrightarrow{A}\) der Ortsvektor eines Aufpunkts (Stützvektor) und \(\overrightarrow{u}\) ein Richtungsvektor der Gerade \(g\).
Gleichung einer Strecke \([AB]\) in Parameterform:
\[\overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{AB}, \; \textcolor{#cc071e}{\lambda \in [0;1]} \]
\[AB \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{AB}; \; \lambda \in \mathbb R\]
Verbindungsvektor \(\overrightarrow{AB}\) berechnen:
\(A(-3|-1|4)\), \(B(0|6|5)\)
\[\overrightarrow{AB} = \overrightarrow{B} - \overrightarrow{A} = \begin{pmatrix} 0 \\ 6 \\ 5 \end{pmatrix} - \begin{pmatrix} -3 \\ -1 \\ 4 \end{pmatrix} = \begin{pmatrix} 3 \\ 7 \\ 1 \end{pmatrix}\]
Eine Gleichung der Gerade \(AB\) lautet somit:
\[AB \colon \overrightarrow{X} = \begin{pmatrix} -2 \\ -1 \\ 4 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 3 \\ 7 \\ 1 \end{pmatrix}; \; \lambda \in \mathbb R\]
Punktprobe \(C \in AB\) durchführen:
Hierfür wird der Ortsvektor \(\overrightarrow{C}\) des Punkte \(C\) und der Ortsvektor \(\overrightarrow{X}\) der Gleichung der Gerade \(AB\) gleichgesetzt. Liest man die Vektorgleichung zeilenweise, ergibt sich ein überbestimmtes lineares Gleichungssystem mit drei Gleichungen und einer zu bestimmenden Unbekannten, dem Parameter \(\lambda\).
Der Punkt \(C\) liegt auf der Gerade \(AB\), wenn das lineare Gleichungssystem für den Parameter \(\lambda\) eine eindeutige Lösung liefert. Andernfalls liegt der Punkt \(C\) nicht auf der Gerade \(AB\).
\(C(3|2|1)\)
\[AB \colon \overrightarrow{X} = \begin{pmatrix} -2 \\ -1 \\ 4 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 3 \\ 7 \\ 1 \end{pmatrix}; \; \lambda \in \mathbb R\]
\[\begin{align*} \overrightarrow{C} &= \overrightarrow{X} \\[0.8em] \begin{pmatrix} 3 \\ 2 \\ 1 \end{pmatrix} &= \begin{pmatrix} -2 \\ -1 \\ 4 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 3 \\ 7 \\ 1 \end{pmatrix} \end{align*}\]
Lineares Gleichungssystem formulieren:
\[\Longrightarrow \quad \begin{cases} 3 = -2 + 3\lambda \quad \Longleftrightarrow \quad \enspace \: 5 = 3\lambda \quad \Longrightarrow \quad \lambda = \frac{5}{3} \\[0.8em] 2 = -1 + 7\lambda \quad \Longleftrightarrow \quad \enspace \: 3 = 7\lambda \quad \Longrightarrow \quad \lambda = \frac{3}{7} \\[0.8em] 1 = \enspace \: 4 + \enspace \lambda \quad \Longleftrightarrow \quad -3 = \enspace \lambda \end{cases}\]
Da sich keine eideutige Lösung für \(\lambda\) ergibt, liegt der Punkt \(C\) nicht auf der Geraden \(AB\). Folglich liegen die drei Punkte \(A\), \(B\) und \(C\) nicht auf einer Geraden.
b) Gleichung der Strecke [AB]
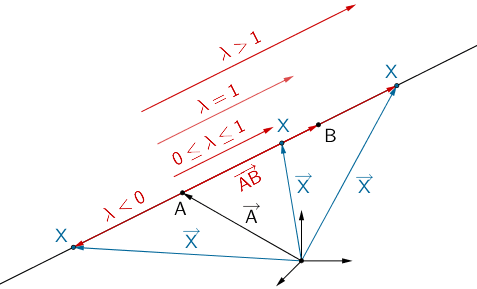
Die Lage eines Punktes \(X\) auf der Gerade \(AB\) hängt vom Wert des Parameters \(\lambda\) ab. Für \(0 \leq \lambda \leq 1\) liegt ein Punkt \(X\) auf der Strecke \([AB]\).
Ausgehend von der Geradengleichung \(AB \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{AB}; \; \lambda \in \mathbb R\) lässt sich eine Gleichung der Strecke \([AB]\) also durch eine geeignete Einschränkung der Werte für den Parameter \(\lambda\) beschreiben.
\[[AB] \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{AB}; \; 0 \leq \lambda \leq 1\]

