- Details
- Kategorie: Analysis 2
Gegeben ist die in \(\mathbb R\) definierte Funktion \(f \colon x \mapsto (1 - x^{2}) \cdot e^{-x}\). Die Abbildung zeigt den Graphen \(G_{f}\) von \(f\).
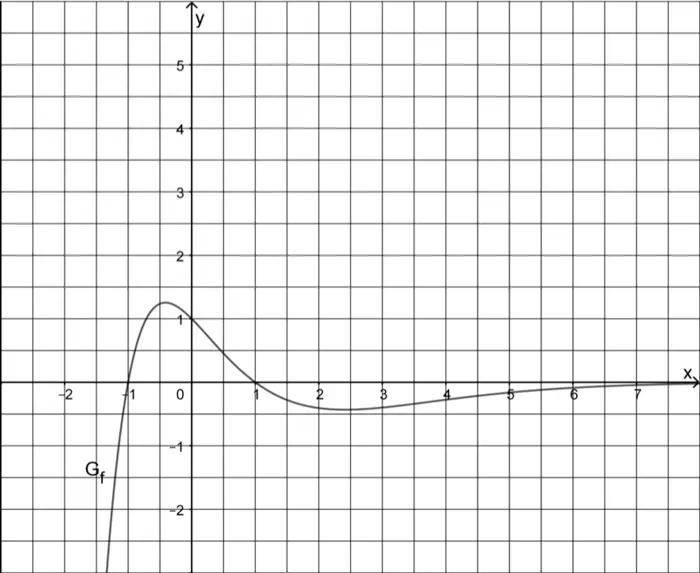
Zeigen Sie, dass \(f\) genau zwei Nullstellen besitzt.
(2 BE)
- Details
- Kategorie: Analysis 2
Bestimmen Sie rechnerisch die \(x\)-Koordinaten der beiden Extrempunkte von \(G_{f}\).
(zur Kontrolle: \(f'(x) = (x^{2} - 2x - 1) \cdot e^{-x}\))
(4 BE)
- Details
- Kategorie: Analysis 2
Ermitteln Sie anhand der Abbildung einen Näherungswert für das Integral \(\displaystyle \int_{-1}^{4}f(x)dx\).
(4 BE)
- Details
- Kategorie: Analysis 2
Die in \(\mathbb R\) definierte Funktion \(F\) ist diejenige Stammfunktion von \(f\), deren Graph durch den Punkt \(T(-1|2)\) verläuft.
Begründen Sie mithilfe der Abbildung, dass der Graph von \(F\) im Punkt \(T\) einen Tiefpunkt besitzt.
(2 BE)
- Details
- Kategorie: Analysis 2
Skizzieren Sie in die Abbildung den Graphen von \(F\). Berücksichtigen Sie dabei insbesondere, dass \(F(1) \approx 3{,}5\) und \(\lim \limits_{x\,\to\,+\infty} F(x) = 2\) gilt.
(3 BE)
- Details
- Kategorie: Analysis 2
Deuten Sie die Aussage \(F(2{,}5) - F(0) \approx 0\) in Bezug auf \(G_{f}\) geometrisch.
(2 BE)
- Details
- Kategorie: Analysis 2
Betrachtet wird nun die Schar der in \(\mathbb R\) definierten Funktionen \(h_{k} \colon x \mapsto (1 - kx^{2}) \cdot e^{-x}\) mit \(k \in \mathbb R\). Der Graph von \(h_{k}\) wird mit \(G_{k}\) bezeichnet. Für \(k = 1\) ergibt sich die bisher betrachtetet Funktion \(f\).
Geben Sie in Abhängigkeit von \(k\) die Anzahl der Nullstellen von \(h_{k}\) an.
(2 BE)
- Details
- Kategorie: Analysis 2
Für einen bestimmten Wert von \(k\) besitzt \(G_{k}\) zwei Schnittpunkte mit der \(x\)-Achse, die voneinander den Abstand 4 haben. Berechnen Sie diesen Wert.
(3 BE)
- Details
- Kategorie: Analysis 2
Beurteilen Sie, ob es einen Wert von \(k\) gibt, sodass \(G_{k}\) und \(G_{f}\) bezüglich der \(x\)-Achse symmetrisch zueinander liegen.
(2 BE)
- Details
- Kategorie: Analysis 2
Betrachtet wird die in \(\mathbb R\) definierte Funktion \(g \colon x \mapsto \dfrac{e^{x}}{e^{x} + 1}\). Ihr Graph wird mit \(G_{g}\) bezeichnet.
Zeigen Sie, dass \(g\) streng monoton zunehmen ist und die Wertemenge \(]0;1[\) besitzt.
(zur Kontrolle: \(g'(x) = \dfrac{e^{x}}{(e^{x} + 1)^{2}}\))
(5 BE)
- Details
- Kategorie: Analysis 2
Geben Sie \(g'(0)\) an un zeichnen Sie \(G_{g}\) im Bereich \(-4 \leq x \leq 4\) unter Berücksichtigung der bisherigen Ergebnisse und der Tatsache, dass \(G_{g}\) in \(W(0|g(0))\) seinen einzigen Wendepunkt hat, in ein Koordinatensystem ein.
(3 BE)
- Details
- Kategorie: Analysis 2
Der Graph der Funktion \(g^{*}\) geht aus \(G_{g}\) durch Strecken und Verschieben hervor. Die Wertemenge von \(g^{*}\) ist \(]-1;1[\). Geben Sie einen möglichen Funktionsterm für \(g^{*}\) an.
(2 BE)
- Details
- Kategorie: Analysis 2
Es wird das Flächenstück zwischen \(G_{g}\) und der \(x\)-Achse im Bereich \(-\ln{3} \leq x \leq b\) mit \(b \in \mathbb R^{+}\) betrachtet. Bestimmen Sie den Wert von \(b\) so. dass die \(y\)-Achse dieses Flächenstück halbiert.
(6 BE)

