Gegeben sind die Funktionen \(f\colon x \mapsto e^{x}\) und \(g\colon x \mapsto \ln{x}\) sowie die Funktion \(h\colon x \mapsto x \cdot e^{x} - 1\).
Es gibt eine Stelle \(x_{T}\), an der der Graph \(G_{f}\) der Funktion \(f\) und der Graph \(G_{g}\) der Funktion \(g\) dieselbe Steigung besitzen.
a) Skizzieren Sie \(G_{f}\) und \(G_{g}\) und Veranschaulichen Sie die Stelle \(x_{T}\) durch Eintragung geeigneter geometrischer Elemente.
b) Begründen Sie rechnerisch, dass \(h(x) = 0\) ein geeigneter Lösungsansatz zur Berechnung von \(x_{T}\) ist. Versuchen Sie nicht, die Gleichung zu lösen!
c) Die Gleichung \(h(x) = 0\) lässt sich näherungsweise mithilfe des Newton-Verfahrens lösen. Begründen Sie, dass \(x_{0} \in [0{,}3;0{,}7]\) ein geeigneter Startwert für die Anwendung des Newton-Verfahrens ist.
d) Berechnen Sie näherungsweise die Stelle \(x_{T}\) gleicher Steigung von \(G_{f}\) und \(G_{g}\), indem Sie den ersten Schritt des Newton-Verfahrens mit dem Startwert \(x_{0} = 0{,}5\) durchführen.
e) Die Gerade \(x = x_{T}\) schneidet \(G_{f}\) im Punkt \(P\) und \(G_{g}\) im Punkt \(Q\). Die Normale \(N_{f}\) durch Punkt \(P\) sowie die Normale \(N_{g}\) durch Punkt \(Q\) schließen mit den Graphen \(G_{f}\) und \(G_{g}\) ein Flächenstück mit dem Flächeninhalt \(A\) ein. Die Gerade \(x = x_{T}\) teilt dieses Flächenstück in zwei gleich große Teilflächen.
Ergänzen Sie Ihre Skizze aus Teilaufgabe a um die Gerade \(x = x_{T}\) sowie die Normalen \(N_{f}\) und \(N_{g}\) und schraffieren Sie das Flächenstück mit dem Flächeninhalt \(A\). Beschreiben Sie sodann die wesentlichen Schritte zur Berechnung des Flächeninhalts \(A\).
a) Skizzieren von \(G_{f}\) und \(G_{g}\) sowie Veranschaulichen der Stelle \(x_{T}\) durch Eintragung geeigneter geometrischer Elemente
Für das Skizzieren der Graphen \(G_{f}\) und \(G_{g}\) sei an dieser Stelle auf die Eigenschaften der Natürlichen Exponential- und Logarithmusfunktion verwiesen (vgl. Abiturskript - 1.3.1 Eigenschaften und Rechenregeln, Natürliche Exponential- und Logarithmusfunktion).
Unter der Steigung des Graphen einer Funktion versteht man die Steigung der Tangente an der betrachteten Stelle.
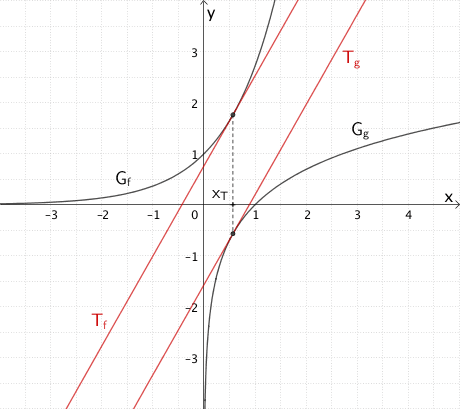
Die Stelle \(x_{T}\) gleicher Steigung der Graphen \(G_{f}\) und \(G_{g}\) ist diejenige Stelle, an der die Tangente \(T_{f}\) an \(G_{f}\) und die Tangente \(T_{g}\) an \(G_{g}\) die gleiche Steigung besitzen, d.h. die Tangenten verlaufen zueinander parallel.
b) Begründung, weshalb \(h(x) = 0\) ein geeigneter Lösungsansatz zur Berechnung von \(x_{T}\) ist
\[f(x) = e^{x}; \; D_{f} = \mathbb R\]
\[g(x) = \ln{x}; \; D_{g} = \mathbb R^{+}\]
\[h(x) = x \cdot e^{x} - 1; \; D_{h} = \mathbb R\]
Die erste Ableitung einer Funktion beschreibt die Steigung einer Tangente an den Graphen der Funktion. Aus der Bedingung gleicher Steigungen der Tangenten \(T_{f}\) und \(T_{g}\) folgt somit der Ansatz:
Anwendung der Differetialrechnung:
Steigung \(m_{T}\) einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\,(\,x_0\,|\,f(x_0)\,)\)
\[m_{T} = f'(x_0)\]
(vgl. Merkhilfe)
\[f'(x) = g'(x)\]
Mit \(f'(x) = e^{x}\) und \(g'(x) = \frac{1}{x}\) (vgl. Abiturskript - 1.5.2 Ableitungsregeln bzw. Merkhilfe) ergibt sich:
Ableitung der natürlichen Exponentialfunktion
\[f(x) = e^x \quad \Longrightarrow \quad f'(x) = e^x\]
Ableitung der natürlichen Logarithmusfunktion
\[f(x) = \ln x \enspace (x > 0) \quad \Longrightarrow \quad f'(x) = \frac{1}{x}\]
(vgl. Merkhilfe)
\[\begin{align*} f'(x) &= g'(x) \\[0.8em] e^{x} &= \frac{1}{x} &&| \cdot x \\[0.8em] x \cdot e^{x} &= 1 &&| - 1 \\[0.8em] x \cdot e^{x} - 1 &= 0 \\[0.8em] h(x) &= 0 \end{align*}\]
Also ist \(h(x) = 0\) ein geeigneter Lösungsansatz zur Berechnung von \(x_{T}\).
c) Begründung weshalb, \(x_{0} \in [0{,}3;0{,}7]\) ein geeigneter Startwert für die näherungsweise Lösung der Gleichung \(h(x) = 0\) mithilfe des Newton-Verfahrens ist
Ein geeigneter Startwert liegt in der Umgebung der Nullstelle von \(h(x)\) (vgl. Abiturskript - 1.5.5 Newton-Verfahren).
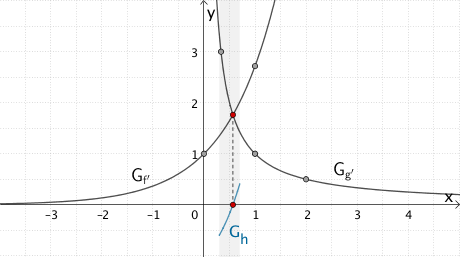
In Teilaufgabe b wurde gezeigt, dass der Ansatz \(f'(x) = g'(x)\) auf die Gleichung \(h(x) = 0\) führt. Eine mit geeigneten Graphenpunkten einfach anzufertigende Skizze zeigt, dass sich die Graphen \(G_{f'}\) der Ableitungsfunktion \(f':x \mapsto e^{x}\) und \(G_{g'}\) der Ableitungsfunktion \(g'\colon x \mapsto \frac{1}{x}\) schneiden. Dies deutet auf eine einfache Nullstelle der Funktion \(h\) hin.
Es ist somit nachzuweisen, dass die Funktion \(h\) im Intervall \([0{,}3;0{,}7]\) das Vorzeichen wechselt.
\[h(x) = x \cdot e^{x} - 1\]
\[h(0{,}3) = 0{,}3 \cdot e^{0{,}3} - 1 \approx -0{,}6\]
\[h(0{,}7) = 0{,}7 \cdot e^{0{,}7} - 1 \approx 0{,}4\]
Also besitzt die Funktion \(h\) im Intervall \([0{,}3;0{,}7]\) eine einfache Nullstelle und \(x_{0} \in [0{,}3;0{,}7]\) ist ein geeigneter Startwert für die näherungsweise Lösung der Gleichung \(h(x) = 0\) mithilfe des Newton-Verfahrens.
d) Durchführung des ersten Schritts des Newton-Verfahrens mit dem Startwert \(x_{0} = 0{,}5\) für die näherungsweise Berechnung die Stelle \(x_{T}\)
Gemäß der Newtonschen Iterationsformel gilt:
Newton-Verfahren
\(x_{n + 1} = x_n - \dfrac{f(x_n)}{f'(x_n)}\) mit \(n \in \mathbb N\) und \(f'(x_n) \neq 0\)
(vgl. Merkhilfe)
\[x_{1} = x_{0} - \frac{h(x_{0})}{h'(x_{0})}\]
Erste Ableitung \(h'\) der Funktion \(h\) bilden:
Die Funktion \(h\) lässt sich mithilfe der Produktregel, der Ableitung der natürlichen Exponentialfunktion, der Ableitung einer Potenzfunktion sowie der Summenregel ableiten.
\[h(x) = x \cdot e^{x} - 1\]
Produktregel
\[f(x) = u(x) \cdot v(x) \quad \Longrightarrow \quad f'(x) = u'(x) \cdot v(x) + u(x) \cdot v'(x)\]
Ableitung der natürlichen Exponentialfunktion
\[ f(x) = e^x \quad \Longrightarrow \quad f'(x) = e^x\]
Ableitung einer Potenzfunktion
\[ f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
Summenregel
\(f(x) = u(x) + v(x) \quad \Longrightarrow \quad f'(x) = u'(x) + v'(x)\)
(vgl. Merkhilfe)
\[h'(x) = 1 \cdot e^{x} + x \cdot e^{x} - 0 = e^{x}(1 + x)\]
Mit \(x_{0} = 0{,}5\) ergibt sich in erster Näherung:
\[x_{1} = 0{,}5 - \frac{h(0{,}5)}{h'(0{,}5)} = 0{,}5 - \frac{0{,}5 \cdot e^{0{,}5} - 1}{e^{0{,}5}(1 + 0{,}5)} \approx 0{,}57\]
An der Stelle \(x_{T} \approx 0{,}57\) besitzen die Graphen \(G_{f}\) und \(G_{g}\) der Funktionen \(f \colon x \mapsto e^{x}\) und \(g\colon x \mapsto \ln{x}\) dieselbe Steigung.
e) Teil1: Einzeichnen der Gerade \(x = x_{T}\), der Normalen \(N_{f}\) und \(N_{g}\) sowie Schraffieren des Flächenstücks mit dem Flächeninhalt \(A\)
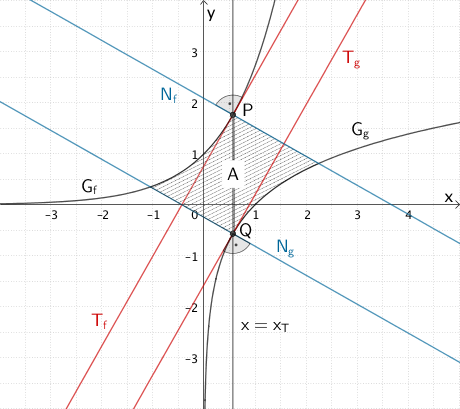
Flächenstück mit dem Flächeninhalt \(A\), welches die Normalen \(N_{f}\) und \(N_{g}\) sowie die Graphen \(G_{f}\) und \(G_{g}\) einschließen. Die Gerade \(x = x_{T}\) teilt das Flächenstück in zwei gleich große Teilflächen (vgl. Angabe).
e) Teil 2: Beschreibung der wesentlichen Schritte zur Berechnung des Flächeninhalts \(A\)
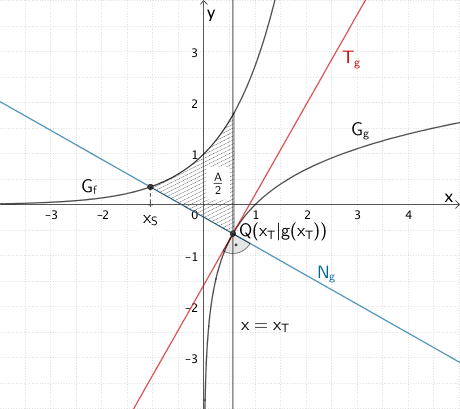
Da die Gerade \(x = x_{T}\) das Flächenstück mit dem Flächeninhalt \(A\) in zwei gleich große Teilflächen teilt, kann für die Berechnung des Flächeninhalt \(A\) beispielsweise das Flächenstück mit dem Flächeninhalt \(\frac{A}{2}\) betrachtet werden, welches der Graph \(G_{f}\), die Normale \(N_{g}\) und die Gerade \(x = x_{T}\) einschließen.
Dann gilt (vgl. Abiturskript - 1.6.4 Flächenberechnung, Flächeninhalt zwischen zwei Funktionsgraphen):
\[A = 2 \cdot \int_{x_{s}}^{x_{T}} \left[ f(x) - N_{g}(x) \right] dx\]
Dabei ist \(x_{S}\) die \(x\)-Koordinate des Schnittpunkts der Normale \(N_{g}\) und des Graphen \(G_{f}\) und \(N_{g}(x)\) der Funktionsterm der Normale \(N_{g}\). Da der Graph \(G_{f}\) für \(x \in [x_{S};x_{T}]\) stets oberhalb der Normale \(N_{g}\) verläuft, ist die Differezfunktion \(f(x) - N_{g}(x)\) positiv, sodass der Betrag des Integrals entfallen kann.
1. Schritt: Funktionsterm der Normale \(N_{g}\) ermitteln
Allgemeine Geradengleichung
\[y = mx + t\]
Wobei \(m\) die Steigung und \(t\) der \(y\)-Achsenabschnitt der Geraden ist.
Ansatz: \(N_{g}(x) = mx + t\)
Anwendung der Differetialrechnung:
Tangentensteigung und Normalensteigung
Tangentensteigung: \(m_{T} = f'(x_0)\)
Normalensteigung: \(m_{N} = -\dfrac{1}{f'(x_0)}\)
(vgl. Merkhilfe)
Es gilt \(m = -\frac{1}{g'(x_{T})}\).
Mit \(Q(x_{T}|g(x_{T})) \in N_{g}\) lässt sich der \(y\)-Achsenabschnitt \(t\) berechnen.
2. Schritt: \(x\)-Koordinate \(x_{S}\) des Schnittpunkts der Normale \(N_{g}\) mit dem Graphen \(G_{f}\) berechnen
\(x_{S}\) ist die untere Integrationsgrenze des zu berechnende bestimmte Integrals \(\displaystyle \int_{x_{s}}^{x_{T}} \left[ f(x) - N_{g}(x) \right] dx\).
Ansatz: \(f(x) = N_{g}(x)\)
Die Gleichung wird nach der Variablen \(x\) aufgelöst und liefert so den Wert für \(x_{S}\).
3. Schritt: Stammfunktion der Differenzfunktion \(f(x) - N_{g}(x)\) bilden
Für die Berechnung des bestimmten Integrals \(\displaystyle \int_{x_{s}}^{x_{T}} \left[ f(x) - N_{g}(x) \right] dx\) wird eine Stammfunktion der Differenzfunktion \(f(x) - N_{g}(x)\) (Integrandenfunktion) benötigt.
Berechnung bestimmter Integrale
\[\int_{a}^{b} f(x)\,dx = [F(x)]_{a}^{b} = F(b) - F(a)\]
Dabei ist \(F\) eine beliebige Stammfunktion zu \(f\).
(vgl. Merkhilfe)
Eigenschaften des bestimmten Integrals - Integrationsregeln
Identische Integrationsgrenzen:
\[\int_{a}^{a} f(x)\,dx = 0\]
Faktorregel:
\(\displaystyle \int_{a}^{b} c \cdot f(x)\,dx = c \cdot \int_{a}^{b} f(x)\,dx\) mit \(c \in \mathbb R\)
Summenregel:
\[\int_{a}^{b} \left[f(x) \pm g(x) \right] dx = \int_{a}^{b}f(x)\,dx \pm \int_{a}^{b}g(x)\,dx\]
Vertauschungsregel:
\[\int_{a}^{b}f(x)\,dx = -\int_{b}^{a}f(x)\,dx\]
Zerlegung in Teilintervalle:
\(\displaystyle \int_{a}^{b}f(x)\,dx = \int_{a}^{c}f(x)\,dx + \int_{c}^{b}f(x)\,dx\) mit \(a \leq c \leq b\)
Diese kann mithilfe der wichtigen unbestimmten Integrale
\( \displaystyle \int e^{x} dx = e^{x} + C\),
\(\displaystyle \int x^r \,dx = \frac{x^{r + 1}}{r + 1} + C \; (r \neq -1)\) und
\( \displaystyle \int c \, dx = c \cdot x + C; \; c \in \mathbb R\)
mit jeweils \(C \in \mathbb R\), gebildet werden (vgl. Abiturskript - 1.6.2 Unbestimmtes Integral).
4. Flächeninhalt \(A\) berechnen
Unter Verwendung der im 3. Schritt ermittelten Stammfunktion wird der Flächeninhalt \(A\) berechnet.
Berechnung bestimmter Integrale
\[\int_{a}^{b} f(x)\,dx = [F(x)]_{a}^{b} = F(b) - F(a)\]
Dabei ist \(F\) eine beliebige Stammfunktion zu \(f\).
(vgl. Merkhilfe)
Eigenschaften des bestimmten Integrals - Integrationsregeln
Identische Integrationsgrenzen:
\[\int_{a}^{a} f(x)\,dx = 0\]
Faktorregel:
\(\displaystyle \int_{a}^{b} c \cdot f(x)\,dx = c \cdot \int_{a}^{b} f(x)\,dx\) mit \(c \in \mathbb R\)
Summenregel:
\[\int_{a}^{b} \left[f(x) \pm g(x) \right] dx = \int_{a}^{b}f(x)\,dx \pm \int_{a}^{b}g(x)\,dx\]
Vertauschungsregel:
\[\int_{a}^{b}f(x)\,dx = -\int_{b}^{a}f(x)\,dx\]
Zerlegung in Teilintervalle:
\(\displaystyle \int_{a}^{b}f(x)\,dx = \int_{a}^{c}f(x)\,dx + \int_{c}^{b}f(x)\,dx\) mit \(a \leq c \leq b\)
\[A = 2 \cdot \int_{x_{s}}^{x_{T}} \left[ f(x) - N_{g}(x) \right] dx\]


