\(N(1{,}6|0|3{,}2)\) ist der Mittelpunkt der Strecke \([KF]\). Begründen Sie, dass die Gerade \(EN\) den Innenwinkel des Dreiecks \(DFE\) bei \(E\) halbiert, und weisen Sie rechnerisch nach, dass \(S\) auf der Geraden \(EN\) liegt.
(4 BE)
Lösung zu Teilaufgabe e
Begründung, dass die Gerade \(EN\) den Innenwinkel des Dreiecks \(DFE\) bei \(E\) halbiert
![Dreieck DFE, Dreieck KFE, Mittelpunkt N der Strecke [KF], Gerade EN, Winkel KEF](/images/stories/B2021_PT_B_G2/B2021_PT_B_G2_e.png)
Planskizze (optional): Wegen \(\textcolor{#e9b509}{\overline{KE}} = \textcolor{#e9b509}{\overline{EF}}\) (vgl. Angabe Teilaufgabe d) ist das Dreieck \(KFE\) gleichschenklig mit der Basis \([KF]\).
Die Gerade \(\textcolor{#cc071e}{EN}\) verläuft durch den Mittelpunkt \(N\) der Basis \([KF]\) und ist somit Symmetrieachse des Dreieck \(KFE\). Folglich halbiert die Gerade \(\textcolor{#cc071e}{EN}\) den Innenwinkel des Dreiecks \(KFE\) und damit auch des Dreiecks \(DFE\) bei \(\textcolor{#e9b509}{E}\) (\(\textcolor{#e9b509}{\measuredangle KFE} = \textcolor{#e9b509}{\measuredangle DFE}\)).
Nachweis, dass \(S\) auf der Gerade \(EN\) liegt
Der Punkt \(S\) ist der Ursprung des Koordinatensystems (vgl. Angabe).
\(S(0|0|0)\)
1. Möglichkeit: Lineare Abhängigkeit der Ortsvektoren \(\overrightarrow{N}\) und \(\overrightarrow{E}\) nachweisen
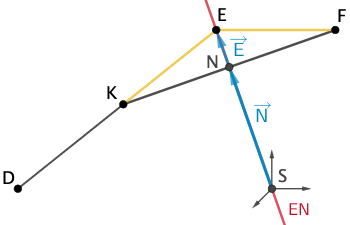
Da der Punkt \(S\) im Ursprung des Koordinatensystems liegt, verläuft die Gerade \(\textcolor{#cc071e}{EN}\) durch \(S\), wenn die Ortsvektoren \(\overrightarrow{SN} = \textcolor{#0087c1}{\overrightarrow{N}}\) und \(\overrightarrow{SE} = \textcolor{#0087c1}{\overrightarrow{E}}\) linear abhängig sind, d. h. ein reelles Vielfaches voneinander sind.
Es ist also beispielsweise die Gültigkeit der Gleichung \(\textcolor{#0087c1}{\overrightarrow{E}} = k \cdot \textcolor{#0087c1}{\overrightarrow{N}}; k \in \mathbb R\) nachzuweisen.
\(N(1{,}6|0|3{,}2)\), \(E(2|0|4)\)
Lineare (Un-)Abhängigkeit von zwei Vektoren
Zwei Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) sind
linear abhängig, wenn
\(\overrightarrow{a} \parallel \overrightarrow{b}\quad\) bzw. \(\quad\overrightarrow{a} = k \cdot \overrightarrow{b}\,; \enspace k \in \mathbb R \quad\) gilt.
linear unabhängig, wenn
\(\overrightarrow{a} \nparallel \overrightarrow{b}\quad\) bzw. \(\quad\overrightarrow{a} \neq k \cdot \overrightarrow{b}\,; \enspace k \in \mathbb R \quad\) gilt.
Lineare (Un-)Abhängigkeit von drei Vektoren
Drei Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{c}\) sind
linear abhängig, wenn
sie in einer Ebene liegen bzw. wenn
die lineare Vektorgleichung \(\overrightarrow{c} = r \cdot \overrightarrow{a} + s \cdot \overrightarrow{b}\) eine eindeutige Lösung hat.
linear unabhängig, wenn
sie den Raum \(\mathbb R^{3}\) aufspannen bzw. wenn
die lineare Vektorgleichung \(\overrightarrow{c} = r \cdot \overrightarrow{a} + s \cdot \overrightarrow{b}\) keine Lösung hat.
Bei der Untersuchung der linearen (Un)Abhängigkeit dreier Vektoren spielt es keine Rolle, welche der drei Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) oder \(\overrightarrow{c}\) man als Linearkombination der beiden anderen Vektoren darzustellen versucht.
\[\textcolor{#0087c1}{\begin{pmatrix} 2 \\ 0 \\ 4 \end{pmatrix}} = k \cdot \textcolor{#0087c1}{\begin{pmatrix} 1{,}6 \\ 0 \\ 3{,}2 \end{pmatrix}} \; \Rightarrow \; \left\{\begin{align*} 2 &= k \cdot1{,}6 \; \Leftrightarrow \; k = \frac{5}{4} \\ 0 &= k \cdot 0 \\ 4 &= k \cdot 3{,}2 \; \Leftrightarrow \; k = \frac{5}{4} \end{align*} \right\} \; \Rightarrow \; S \in \textcolor{#cc071e}{EN}\]
Es gilt \(\textcolor{#0087c1}{\overrightarrow{E}} = \dfrac{5}{4} \cdot \textcolor{#0087c1}{\overrightarrow{N}}\). Also liegt \(S\) auf der Gerade \(\textcolor{#cc071e}{EN}\).
2. Möglichkeit: Punktprobe mit Gleichung der Gerade \(EN\)
Gleichung der Gerade \(\textcolor{#cc071e}{EN}\) in Parameterform beschreiben:
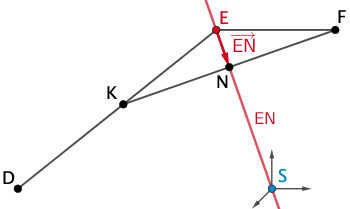
Planskizze (optional): Beispielsweise ist \(\textcolor{#cc071e}{E}\) ein Aufpunkt und \(\textcolor{#cc071e}{\overrightarrow{EN}}\) ein Richtungsvektor der Geradengleichung in Parameterform.
\(N(1{,}6|0|3{,}2)\), \(E(2|0|4)\)
Gleichung einer Gerade / Strecke in Parameterform
Jede Gerade \(g\) kann durch eine Gleichung in der sogenannten Parameterform
\(g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u} \enspace\) mit dem Parameter \(\lambda \in \mathbb R\) beschrieben werden.
Dabei ist \(\overrightarrow{A}\) der Ortsvektor eines Aufpunkts (Stützvektor) und \(\overrightarrow{u}\) ein Richtungsvektor der Gerade \(g\).
Gleichung einer Strecke \([AB]\) in Parameterform:
\[\overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{AB}, \; \textcolor{#cc071e}{\lambda \in [0;1]} \]
\[\textcolor{#cc071e}{\overrightarrow{EN}} = \overrightarrow{N} - \overrightarrow{E} = \begin{pmatrix} 1{,}6 \\ 0 \\ 3{,}2 \end{pmatrix} - \begin{pmatrix} 2 \\ 0 \\ 4 \end{pmatrix} = \textcolor{#cc071e}{\begin{pmatrix} -0{,}4 \\0 \\ -0{,}8 \end{pmatrix}}\]
\[\begin{align*} &\textcolor{#cc071e}{EN}\colon \overrightarrow{X} = \textcolor{#cc071e}{\overrightarrow{E}} + \mu \cdot \textcolor{#cc071e}{\overrightarrow{EN}}, \; \mu \in \mathbb R \\[0.8em] &\textcolor{#cc071e}{EN} \colon \overrightarrow{X} =\textcolor{#cc071e}{\begin{pmatrix} 2 \\ 0 \\ 4 \end{pmatrix}} + \mu \cdot \textcolor{#cc071e}{\begin{pmatrix} -0{,}4 \\0 \\ -0{,}8 \end{pmatrix}}, \; \mu \in \mathbb R\end{align*}\]
Punktprobe \(\textcolor{#0087c1}{S(0|0|0)} \in \textcolor{#cc071e}{EN}\):
\[\textcolor{#0087c1}{\begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}} =\textcolor{#cc071e}{\begin{pmatrix} 2 \\ 0 \\ 4 \end{pmatrix}} + \mu \cdot \textcolor{#cc071e}{\begin{pmatrix} -0{,}4 \\0 \\ -0{,}8 \end{pmatrix}} \;\Rightarrow \; \left\{ \begin{align*} 0 &= 2 - 0{,}4\mu \; \Leftrightarrow \; \mu = 5 \\ 0 &= 0 \\ 0 &= 4 - 0{,}8\mu \;\Leftrightarrow \; \mu = 5 \end{align*} \right\} \; \Rightarrow \; \textcolor{#0087c1}{S} \in \textcolor{#cc071e}{EN}\]
\(\mu = 5\) ist eindeutige Lösung der Vektorgleichung. Somit liegt der Punkt \(\textcolor{#0087c1}{S}\) auf der Gerade \(\textcolor{#cc071e}{EN}\).
