Gegeben ist die Funktion \(f \colon x \mapsto \sqrt{x + 3}\) mit Definitionsmenge \(D_f\). Abbildung 1 zeigt den Graphen \(G_f\) von \(f\), einen beliebigen Punkt \(Q(x|f(x))\) auf \(G_f\) sowie den Punkt \(P(1{,}5|0)\) auf der \(x\)-Achse.
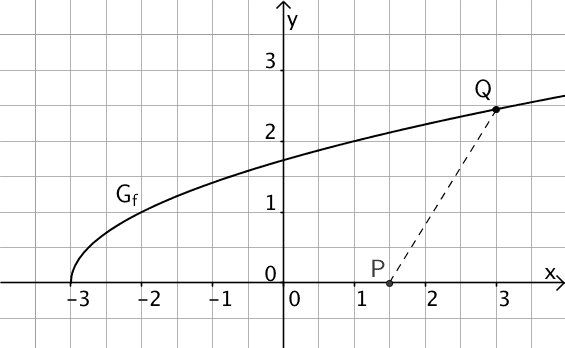Abb. 1
Begründen Sie, dass \(D_f = [-3;+\infty[\) die maximale Definitionsmenge von \(f\) ist. Wie geht \(G_f\) aus dem Graphen der in \(\mathbb R_0^+\) definierten Funktion \(w : x \mapsto \sqrt{x\;}\;\) hervor?
(2 BE)
Lösung zu Teilaufgabe 1a
Maximale Definitionsmenge \(D_f\)
\[f(x) = \sqrt{x + 3}\]
Der Wertebereich des Radikanden bestimmt die maximale Definitionsmenge \(D_f\).
\[x + 3 \geq 0 \quad \Longleftrightarrow \quad x \geq -3\]
\[\Longrightarrow \quad D_f = [-3; +\infty[\]
Entstehung von \(G_f\) aus \(G_w\)
\[f(x) = \sqrt{x + 3} \hspace{100px} w(x) = \sqrt{x}\]
Verschieben von Funktionsgraphen
\[g(x) = f(x +a) + b\]
Verschiebung in \(x\)-Richtung um \(-a\), Verschiebung in \(y\)-Richtung um \(b\)
\(G_f\) geht aus \(G_w\) durch Verschiebung um \(-3\) in \(x\)-Richtung hervor.
