Geben Sie jeweils den Term einer in \(\mathbb R\) definierten Funktion an, die die angegebene Eigenschaft besitzt.
Der Graph der Funktion \(f\) hat den Hochpunkt \((0|5)\,\).
(2 BE)
Lösung zu Teilaufgabe 2a
Betrachtung bekannter Grundtypen von Funktionen:
Potenzfunktion mit natürlichem geraden Exponenten
\[f(x) = ax^n + 5\,, \enspace D = \mathbb R\,, \enspace a < 0\,, \enspace n = 2k\,, \enspace k \in \mathbb N\]
Der Graph von \(f\) ist eine nach unten geöffnete Parabel n-ter Ordnung mit dem Scheitelpunkt \(S\,(0|5)\), welcher absoluter Hochpunkt von \(f\) ist.
Beispiele:
\[f_1(x) = -x^2 + 5\]
\[f_2(x) = -2x^4 + 5\]
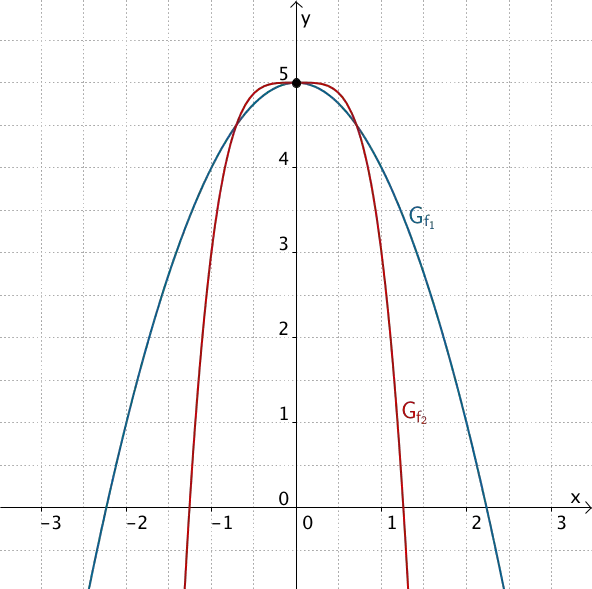
Graphen der Potenzfunktionen \(f_1\) und \(f_2\)
Allgemeine Kosinusfunktion
Allgemeine Kosinusfunktion
\[f(x) = a \cdot \cos(bx + c) + d = a \cdot \cos \left[b \left(x + \frac{c}{b} \right) \right] + d\]
\[a,b,c,d \in \mathbb R\;; \quad a,b \neq 0\;; \quad x \in \mathbb R\]
Streckung um \(a\) in \(y\)-Richtung
Streckung um \(\displaystyle \frac{1}{b}\) in \(x\)-Richtung, Periode: \(\displaystyle p = \frac{2\pi}{\vert b \vert}\)
Verschiebung um \(\displaystyle -\frac{c}{b}\) in \(x\)-Richtung
Verschiebung um \(d\) in \(y\)-Richtung
\[f(x) = a \cdot \cos (bx + c) + d\,, \enspace D = \mathbb R\,, \enspace a,b,c,d \in \mathbb R\,, \enspace a,b \neq 0\]
Die Parameter \(a\) und \(d\) bestimmen die \(y\)-Koordinate der Hochpunkte einer allgemeinen Kosinusfunktion. Es muss gelten: \(\,a + d = 5\,\).
Der Parameter \(b\) streckt bzw. staucht die Kosinusfunktion in \(x\)-Richtung. Er hat auf einen Hochpunkt an der Stelle \(x = 0\) keinen Einfluss.
Eine mögliche Verschiebung in \(x\)-Richtung um \(\displaystyle -\frac{c}{b}\) muss gleich einem ganzzahligen Vielfachen der Periodenlänge \(\displaystyle \frac{2\pi}{\vert b \vert}\) sein.
Beispiele:
\[f_3(x) = 5 \cdot \cos x\]
\[f_4(x) = 2 \cdot \cos (2x + 2\pi) + 3 = 2 \cdot \cos \left[2(x + \pi)\right] + 3\]
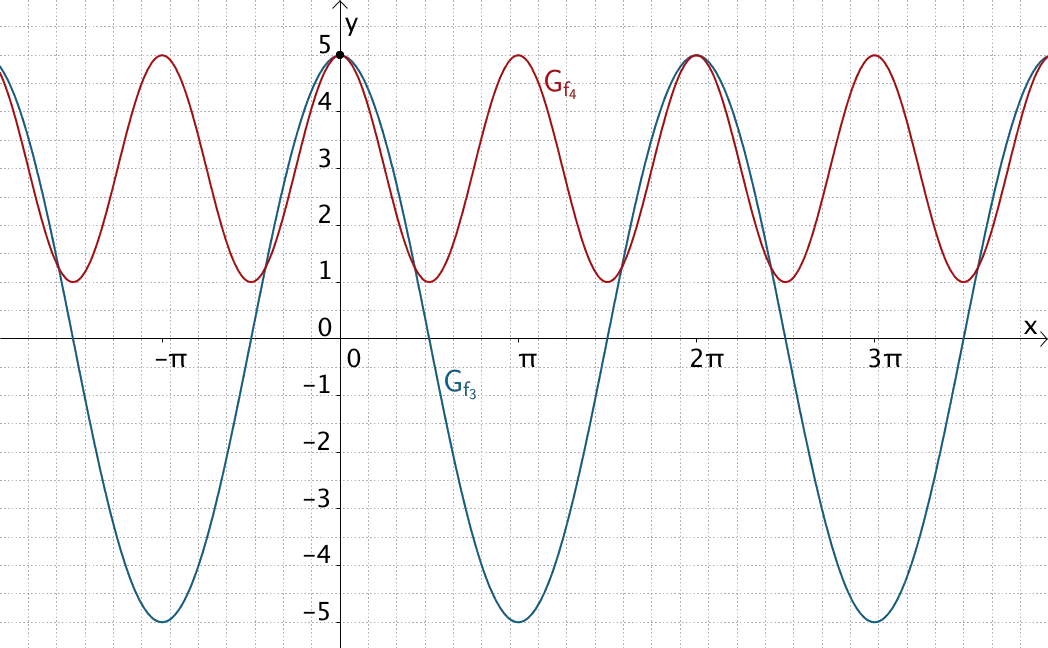
Graphen der Kosinusfunktionen \(f_3\) und \(f_4\)


