Die Punkte \(A(3|3{,}6)\) und \(B(8|0{,}8)\) liegen auf \(G_{f}\); zwischen diesen beiden Punkten verläuft \(G_{f}\) unterhalb der Strecke \([AB]\).

Skizzieren Sie \(G_{f}\) im Bereich \(-10 \leq x \leq 10\) unter Verwendung der bisherigen Informationen in einem Koordinatensystem.

(4 BE)

Lösung zu Teilaufgabe 1c

 

\[f(x) = \frac{6x}{x^{2} - 4}; \; D_{f} = \mathbb R \backslash \{-2;2\}\]

 

Bisherige Informationen:

  • \(G_{f}\) ist punktsymmetrisch zum Koordinatenursprung (vgl. Angabe Aufgabe 1).
  • Die Geraden mit den Gleichungen \(\textcolor{#e9b509}{x = -2}\) und \(\textcolor{#e9b509}{x = 2}\) sind senkrechte Asymptoten von \(G_{f}\) (vgl. Teilaufgabe 1a).
  • Die \(\bf{x}\)-Achse ist waagrechte Asymptote von \(G_{f}\) (vgl. Teilaufgabe 1a).
  • \(G_{f}\) ist in den drei Teilintervallen \(]-\infty;-2[\), \(]-2;2[\) und \(]2;+\infty[\) jeweils streng monoton fallend (vgl. Teilaufgabe 1b).
  • Die Tangente an \(G_{f}\) im Punkt \(\textcolor{#cc071e}{(0|f(0))}\) (\(f(0) = 0\)) hat die Steigung \(\textcolor{#cc071e}{m = -1{,}5}\) (vgl. Teilaufgabe 1b).
  • \(G_{f}\) verläuft durch die Punkte \(\bf{A(3|3{,}6)}\) und \(\bf{B(8|0{,}8)}\) (vgl. Angabe Teilaufgabe 1c).

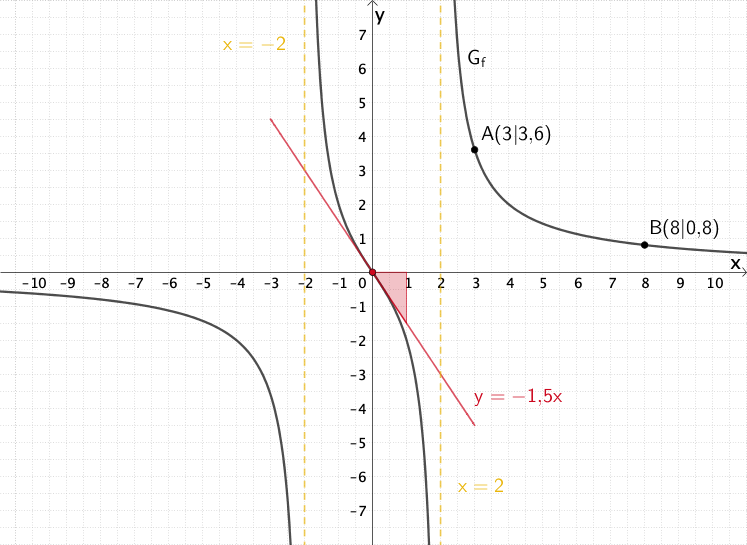
Skizze des Graphen der Funktion f im Bereich -10 ≤ x ≤ 10 unter Verwendung der bisherigen Informationen

Skizze von \(G_{f}\) im Bereich \(-10 \leq x \leq 10\) unter Verwendung der bisherigen Informationen

 

Mögliche Vorgehensweise (nicht verlangt)

Unter Berücksichtigung der senkrechten Asymptote mit der Gleichung \(\textcolor{#e9b509}{x = 2}\) und der \(\bf{x}\)-Achse als waagrechte Asymptote sowie des Monotonieverhaltens von \(f\) (streng monoton fallend) wird der Verlauf von \(G_{f}\) im Teilintervall \(\boldsymbol{]2;+\infty[}\) durch die Punkte \(\bf{A(3|3{,}6)}\) und \(\bf{B(8|0{,}8})\) skizziert.

Die Punktsymmetrie von \(\bf{G_{f}}\) bezüglich des Koordinatenursprungs ermöglicht die Skizze von \(G_{f}\) im Teilintervall \(\boldsymbol{]-\infty;-2[}\).

Aufgrund des Monotonieverhaltens von \(f\) (streng monoton fallend) sowie der Steigung \(\textcolor{#cc071e}{m = -1{,}5}\) der Tangente an \(G_{f}\) im Punkt \(\textcolor{#cc071e}{(0|f(0))}\) (f(0) = 0) lässt sich \(G_{f}\) im Teilintervall \(\boldsymbol{]-2;2[}\) skizzieren.