- Details
- Kategorie: Analysis 1
Gegeben ist die Funktion \(h \colon x \mapsto x \cdot \ln{(x^{2})}\) mit maximalem Definitionsbereich \(D_{h}\).
Geben Sie \(D_{h}\) an und zeigen Sie, dass für den Term der Ableitungsfunktion \(h'\) gilt: \(h'(x) = \ln{(x^{2})} + 2\).
(2 BE)
- Details
- Kategorie: Analysis 1
Bestimmen Sie die Koordinaten des im II. Quadranten liegenden Hochpunkts des Graphen von \(h\).
(3 BE)
- Details
- Kategorie: Analysis 1
Die Abbildung 1 zeigt den Graphen \(G_{f'}\) der Ableitungsfunktion \(f'\) einer in \(\mathbb R\) definierten ganzrationalen Funktion \(f\). Nur in den Punkten \((-4|f'(-4))\) und \((5|f'(5))\) hat der Graph \(G_{f'}\) waagrechte Tangenten.
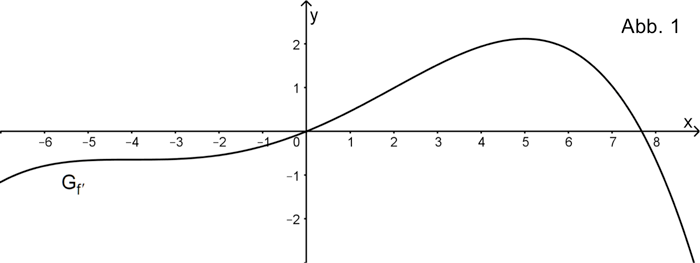
Begründen Sie, dass \(f\) genau eine Wendestelle besitzt.
(2 BE)
- Details
- Kategorie: Analysis 1
Es gibt Tangenten an den Graphen von \(f\), die parallel zur Winkelhalbierenden des I. und III. Quadranten sind. Ermitteln Sie anhand des Graphen \(\mathbf{G_{f'}}\) der Ableitungsfunktion \(f'\) in der Abbildung 1 Näherungswerte für die \(x\)-Koordinaten derjenigen Punkte, in denen der Graph von \(f\) jeweils eine solche Tangente hat.
(2 BE)
- Details
- Kategorie: Analysis 1
Gegeben sind die in \(\mathbb R\) definierten Funktionen \(f \colon x \mapsto x^{2} + 4\) und \(g_{m} \colon x \mapsto m \cdot x\) mit \(m \in \mathbb R\). Der Graph von \(f\) wird mit \(G_{f}\) und der Graph von \(g_{m}\) mit \(G_{m}\) bezeichnet.
Skizzieren Sie \(G_{f}\) in einem Koordinatensystem. Berechnen Sie die Koordinaten des gemeinsamen Punkts der Graphen \(G_{f}\) und \(G_{4}\).
(3 BE)
- Details
- Kategorie: Analysis 1
Es gibt Werte von \(m\), für die die Graphen \(G_{f}\) und \(G_{m}\) jeweils keinen gemeinsamen Punkt haben. Geben Sie diese Werte von \(m\) an.
(2 BE)
- Details
- Kategorie: Analysis 1
Gegeben ist die Funktion \(g\) mit \(g(x) = 0{,}7 \cdot e^{0{,}5x} - 0{,}7\) und \(x \in \mathbb R\). Die Funktion \(g\) ist umkehrbar. Die Abbildung 2 zeigt den Graphen \(G_{g}\) von \(g\) sowie einen Teil des Graphen \(G_{h}\) der Umkehrfunktion \(h\) von \(g\).
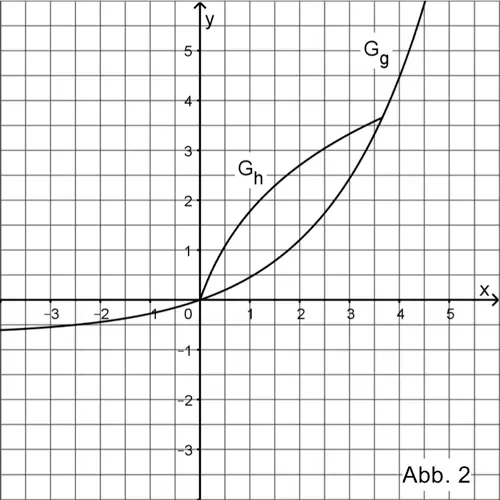
Zeichnen Sie in die Abbildung 2 den darin fehlenden Teil von \(G_{h}\) ein.
(2 BE)
- Details
- Kategorie: Analysis 1
Betrachtet wird das von den Graphen \(G_{g}\) und \(G_{h}\) eingeschlossene Flächenstück. Schraffieren Sie den Teil dieses Flächenstücks, dessen Inhalt mit dem Term \(\displaystyle 2 \cdot \int_{0}^{2{,}5} (x - g(x))dx\) berechnet werden kann.
(2 BE)
- Details
- Kategorie: Analysis 1
Geben Sie den Term einer Stammfunktion der in \(\mathbb R\) definierten Funktion \(k \colon x \mapsto x - g(x)\) an.
(2 BE)


