Abbildung 2 zeigt ein Haus mit einer Dachgaube, deren Vorderseite schematisch in Abbildung 3 dargestellt ist. Die Vorderseite wird modellhaft durch das Flächenstück beschrieben, das der Graph \(G_f\) der Funktion \(f\) aus Aufgabe 1, die \(x\)-Achse und die Geraden mit den Gleichungen \(x = -4\) und \(x = 4\) einschließen. Dabei entspricht eine Längeneinheit im Koordinatensystem einem Meter in der Realität.
Abb. 2
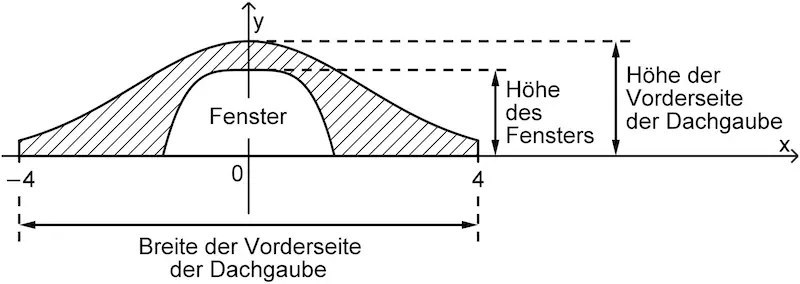Abb. 3
Geben Sie die Breite und Höhe der Vorderseite der Dachgaube an.
(2 BE)
Lösung zu Teilaufgabe 2a
Breite der Vorderseite: 8 m
Höhe der Vorderseite: 2 m
Ausführliche Erklärung (nicht verlangt)
Die Breite der Vorderseite der Dachgaube wird im Modell durch die Geraden mit den Gleichungen \(x = -4\) und \(x = 4\) begrenzt (vgl. Angabe). Der Abstand der Geraden ergibt sich zu \(4 - (-4) = \textcolor{#e9b509}{8}\) Längeneinheiten. Da eine Längeneinheit in der Realität einem Meter entspricht, ist die Vorderseite der Dachgaube 8 m breit.
Im Modell beschreibt der Graph der Funktion \(f\) aus Aufgabe 1 die obere Profillinie der Vorderseite der Dachgaube. Aus Teilaufgabe 1a ist \(f(0) = \textcolor{#e9b509}{2}\) bekannt, d. h., der Graph von \(f\) schneidet die \(y\)-Achse im Punkt \((0|\textcolor{#e9b509}{2})\). Die Vorderseite der Dachgaube ist damit 2 m hoch.
