Lagebeziehung Gerade - Kugel
Die gegenseitige Lage zwischen einer Geraden \(g\) und einer Kugel \(K\) mit dem Mittelpunkt \(M\) wird durch den Abstand \(d(M;g)\) des Mittelpunktes \(M\) von der Geraden \(g\) bestimmt. Dieser Abstand kann, wie in Abschnitt Abiturskript - 2.4.1 Abstand Punkt - Gerade beschrieben, ermittelt werden.
Es lassen sich drei Fälle unterscheiden:
Die Gerade \(g\) und die Kugel \(K\) haben keinen gemeinsamen Punkt.
\[d(M;g) > r\]
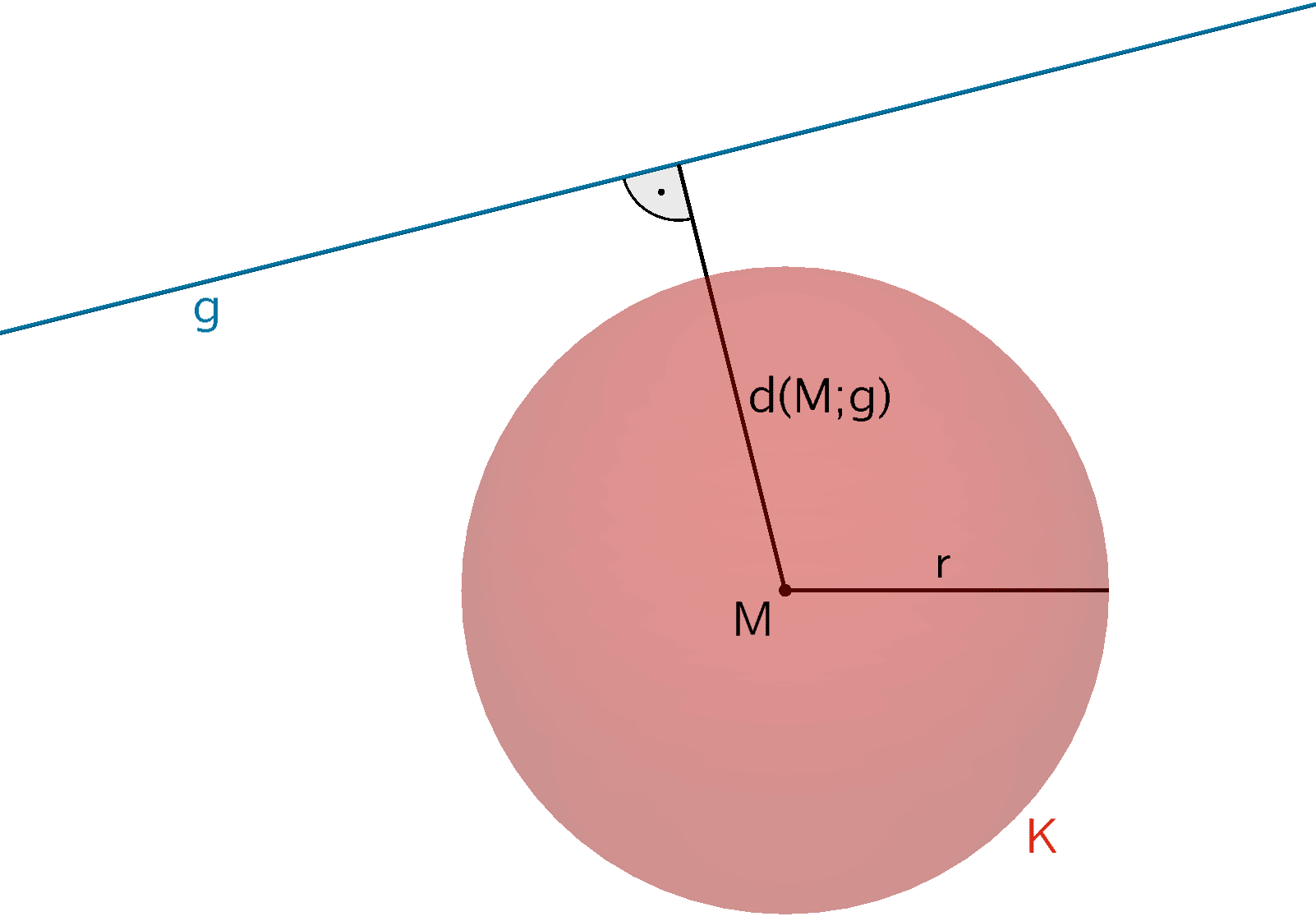
Die Gerade \(g\) und die Kugel \(K\) haben eine gemeinsamen Punkt (Berührpunkt).
\[d(M;g) = r\]
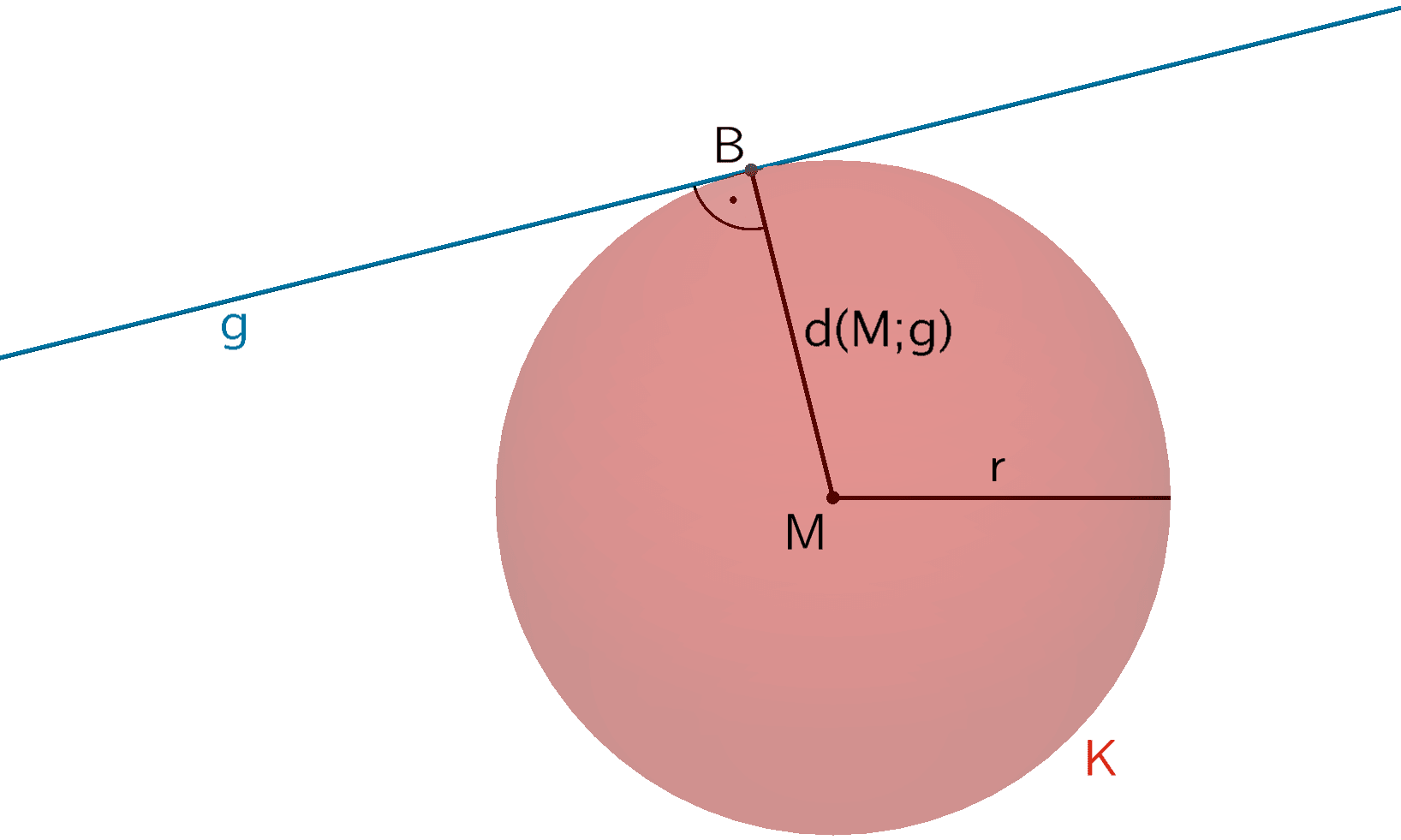
Die Gerade \(g\) und die Kugel \(K\) haben zwei gemeinsame Punkte (Schnittpunkte).
\[d(M;g) < r\]
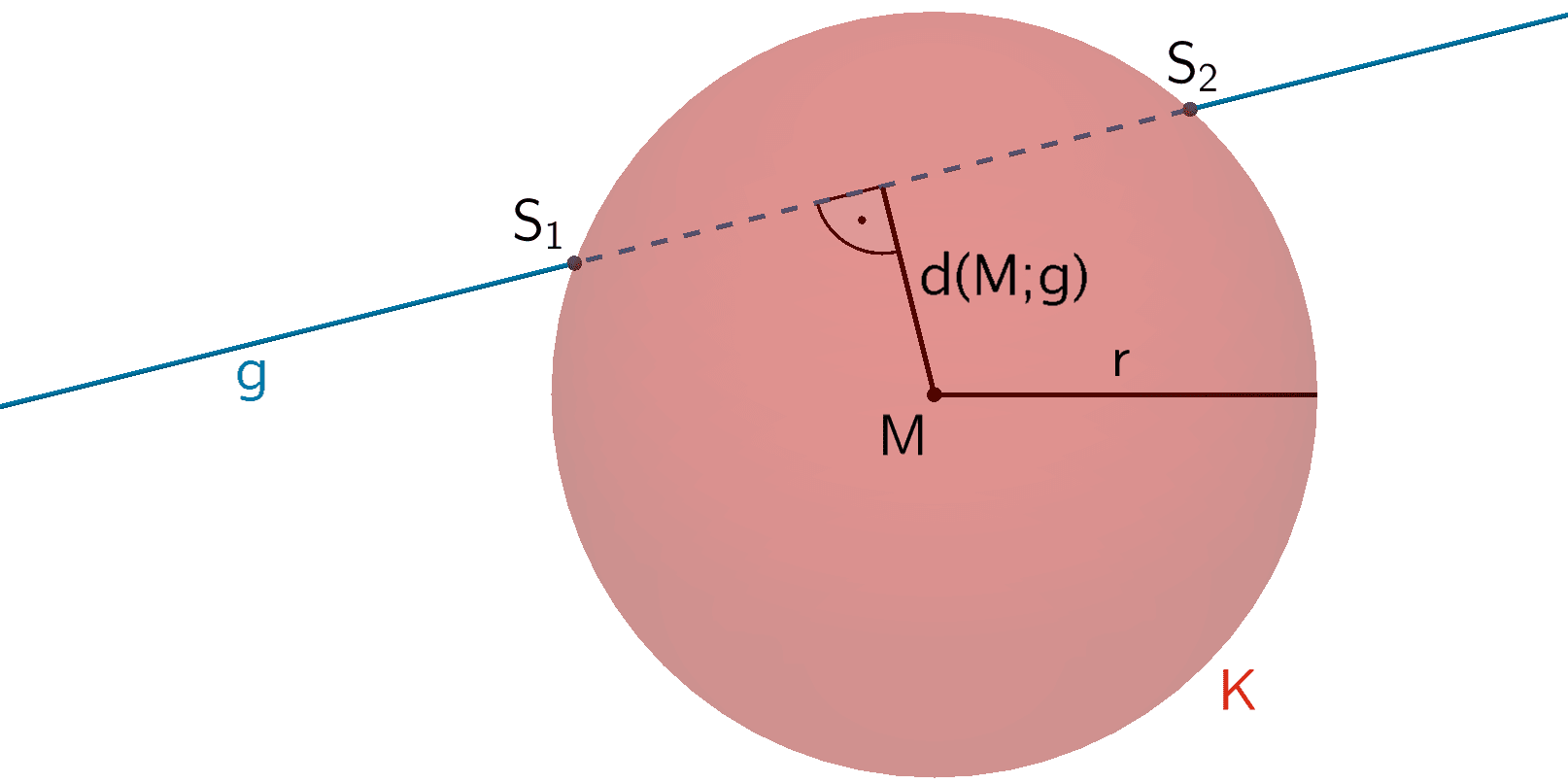
Bestimmung der gemeinsamen Punkte einer Geraden mit einer Kugel
Die gemeinsamen Punkte einer Geraden \(g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u}\,; \; \lambda \in \mathbb R\) und einer Kugel \(K \colon (x_{1} - m_{1})^{2} + (x_{2} - m^{2})^{2} + (x_{3} - m_{3})^{2} = r^{2}\) erhält man, indem man die Koordinaten des Ortsvektors \(\overrightarrow{X}\) der Geradengleichung von \(g\) in die Gleichung der Kugel \(K\) einsetzt.
Es ergibt sich eine quadratische Gleichung für \(\lambda\), die keine Lösung, genau eine Lösung oder zwei Lösungen haben kann (vgl. Abiturskript - 1.1.2 Quadratische Funktion, Nullstellen).
Keine Lösung
\(\Longrightarrow \quad\)\(g\) und \(K\) haben keine gemeinsamen Punkte.
Genau eine Lösung für \(\lambda\)
\(\Longrightarrow \quad\)\(g\) und \(K\) haben einen gemeinsamen Berührpunkt \(B\).
Zwei Lösungen für \(\lambda\)
\(\Longrightarrow \quad\)\(g\) und \(K\) haben zwei gemeinsame Schnittpunkte \(S_{1}\) und \(S_{2}\).
Für die Berechnung der Koordinaten der gemeinsamen Punkte setzt man die ermittelten Werte des Parameters \(\lambda\) in die Gleichung der Geraden \(g\) ein.
Dieses Verfahren eignet sich anstelle der Bestimmung des Abstands \(d(M;g)\) des Kugelmittelpunkts \(M\) von der Geraden \(g\) als Alternative, um die Lagebeziehung einer Geraden zu einer Kugel zu untersuchen.
Beispielaufgabe
Gegeben seien die Gerade \(g \colon \overrightarrow{X} = \begin{pmatrix} -3 \\ 1 \\ 3 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}; \; \lambda \in \mathbb R \) sowie die Kugel \(K \colon (x_{1} - 3)^{2} + (x_{2} - 3)^{2} + (x_{3} - 3)^{2} = 16\).
Untersuchen Sie die gegenseitige Lage der Geraden \(g\) und der Kugel \(K\) und bestimmen Sie ggf. die Koordinaten der gemeinsamen Punkte.
Da die Aufgabenstellung neben der Lagebeziehung auch nach den Koordinaten möglicher gemeinsamer Punkte fragt, wird der Ansatz zur Bestimmung der gemeinsamen Punkte einer Geraden und einer Kugel gewählt.
\[g \colon \overrightarrow{X} = \begin{pmatrix} -3 \\ 1 \\ 3 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}; \; \lambda \in \mathbb R\]
\[K \colon (x_{1} - 3)^{2} + (x_{2} - 3)^{2} + (x_{3} - 3)^{2} = 16\]
Koordinaten des Ortsvektors \(\overrightarrow{X}\) der Geradengleichung von \(g\) in die Gleichung der Kugel \(K\) einsetzen:
\[\begin{align*}g \cap K \colon (-3 + \lambda - 3)^{2} + (1 + \lambda - 3)^{2} + (3 - 3)^{2} &= 16 \\[0.8em] (-6 + \lambda)^{2} + (-2 + \lambda)^{2} &= 16 \\[0.8em] 36 - 12\lambda + \lambda^{2} + 4 - 4\lambda + \lambda^{2} &= 16 \\[0.8em] 2\lambda^{2} - 16\lambda + 40 &= 16 & &| - 16 \\[0.8em] 2\lambda^{2} -16\lambda + 24 &= 0 & &| : 2 \\[0.8em] \lambda^{2} - 8\lambda + 12 &= 0 \end{align*}\]
Lösungsformel für quadratische Gleichungen anwenden (vgl. Abiturskript - 1.1.2 Quadratische Funktion, Nullstellen):
\[\begin{align*} \lambda_{1,2} &= \frac{8 \pm \sqrt{(-8)^{2} - 4 \cdot 1 \cdot 12}}{2 \cdot 1} \\[0.8em] &= \frac{8 \pm \sqrt{16}}{2} \\[0.8em] &= 4 \pm 2 \end{align*}\]
\[\lambda_{1} = 2; \, \lambda_{2} = 6\]
\(\Longrightarrow \quad\)Die Gerade \(g\) schneidet die Kugel \(K\).
Koordinaten der Schnittpunkte berechnen:
Hierfür werden die ermittelten Werte des Parameters \(\lambda\) in die Gleichung der Geraden \(g\) eingesetzt.
\[g \colon \overrightarrow{X} = \begin{pmatrix} -3 \\ 1 \\ 3 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}; \; \lambda \in \mathbb R\]
\[\lambda_{1} = 2; \, \lambda_{2} = 6\]
\[\overrightarrow{S}_{1} = \begin{pmatrix} -3 \\ 1 \\ 3 \end{pmatrix} + 2 \cdot \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix} = \begin{pmatrix} -1 \\ 3 \\ 3 \end{pmatrix}\]
\[\Longrightarrow \quad S_{1}(-1|3|3)\]
\[\overrightarrow{S}_{2} = \begin{pmatrix} -3 \\ 1 \\ 3 \end{pmatrix} + 6 \cdot \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix} = \begin{pmatrix} 3 \\ 7 \\ 3 \end{pmatrix}\]
\[\Longrightarrow \quad S_{2}(3|7|3)\]


