Berechnen Sie die Höhen, in denen das Loch gebohrt werden kann, damit die Spritzweite 6 m beträgt. Geben Sie zudem die Höhe an, in der das Loch gebohrt werden muss, damit die Spritzweite maximal ist.
(5 BE)
Lösung zu Teilaufgabe j
\(x\): Höhe des Bohrlochs über dem Speicherboden in Metern
\(f(x)\): Spritzweite in Metern
\[f(x) = 2 \cdot \sqrt{10x - x^2}\]
Berechnung der Höhen, in denen das Loch gebohrt werden kann, damit die Spritzweite 6 m beträgt
Bedingung: \(f(x) = 6\)
\[\begin{align*} f(x) &= 6 \\[0.8em] 2 \cdot \sqrt{10x - x^2} &= 6 &&| : 2 \\[0.8em] \sqrt{10x - x^2} &= 3 &&| \; (\dots)^2\;\text{(Quadrieren)} \\[0.8em] 10x - x^2 &= 9 &&| - 9\;\text{(quadratische Gleichung formulieren)} \\[0.8em] \textcolor{#cc071e}{-}x^2 + \textcolor{#0087c1}{10}x \textcolor{#e9b509}{- 9} &= 0 &&| \; \text{Mitternachtsformel anwenden} \end{align*}\]
Lösungsformel für quadratische Gleichungen (vgl. Merkhilfe)
\[ax^2 + bx + c = 0 \,, \qquad a, b, c \in \mathbb R \,, \quad a \neq 0\]
\[\begin{align*} x_{1,2} &= \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}, \quad b^2 \geq 4ac \\[0.8em] x_{1,2} &= \frac{-b \pm \sqrt{D}}{2a}, \quad D \geq 0 \end{align*}\]
Diskriminante \(D = b^2 -4ac \;\):
\(D < 0\,\): keine Lösung
\(D = 0\,\): genau eine Lösung
\(D > 0\,\): zwei verschiedene Lösungen
\[\begin{align*}x_{1,2} &= \frac{-\textcolor{#0087c1}{10} \pm \sqrt{\textcolor{#0087c1}{10}^2 - 4 \cdot \textcolor{#cc071e}{(-1)} \cdot \textcolor{#e9b509}{(-9)}}}{2 \cdot \textcolor{#cc071e}{(-1)}} \\[0.8em] &= \frac{-10 \pm \sqrt{64}}{-2} = \frac{-10 \pm 8}{-2} = 5 \pm 4 \\[0.8em] x_1 &= 1; \; x_{2} = 9 \end{align*}\]
Damit die Spritzweite 6 Meter beträgt, kann das Loch in den Höhen 1 m und 9 m gebohrt werden.
Höhe, in der das Loch gebohrt werden muss, damit die Spritzweite maximal ist
Damit die Spritzweite maximal ist, muss das Loch in 5 Meter Höhe gebohrt werden.
Begründung (nicht verlangt)
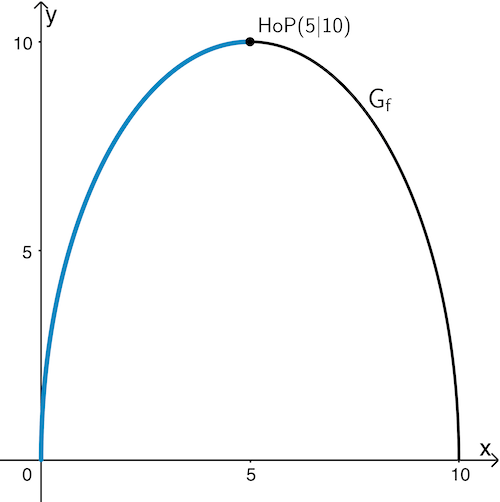
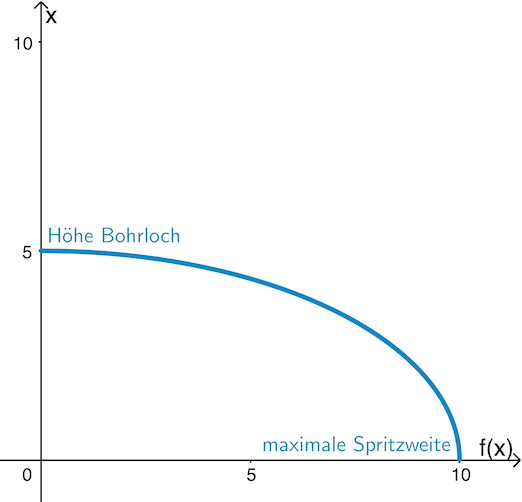
Die Spritzweite wird modellhaft durch die in den bisherigen Teilaufgaben behandelte Funktion \(f\) beschrieben (vgl. Angabe). Aus Teilaufgabe b ist bekannt, dass \(G_f\) den Hochpunkt \((5|10)\) besitzt. Daraus ergibt sich für ein Bohrloch in 5 Meter Höhe die maximale Spritzweite von 10 Metern.


