Der Punkt \(R\) aus Aufgabe 3d entspricht demjenigen Punkt der Tunnelwand, der im betrachteten Querschnitt vom Hangprofil den kleinsten Abstand \(e\) in Metern hat. Beschreiben Sie die wesentlichen Schritte eines Verfahrens zur rechnerischen Ermittlung von \(e\).
(3 BE)
Lösung zu Teilaufgabe 3e
Gleichung einer Normale, Schnittpunkt zweier Geraden, Abstand zweier Punkte
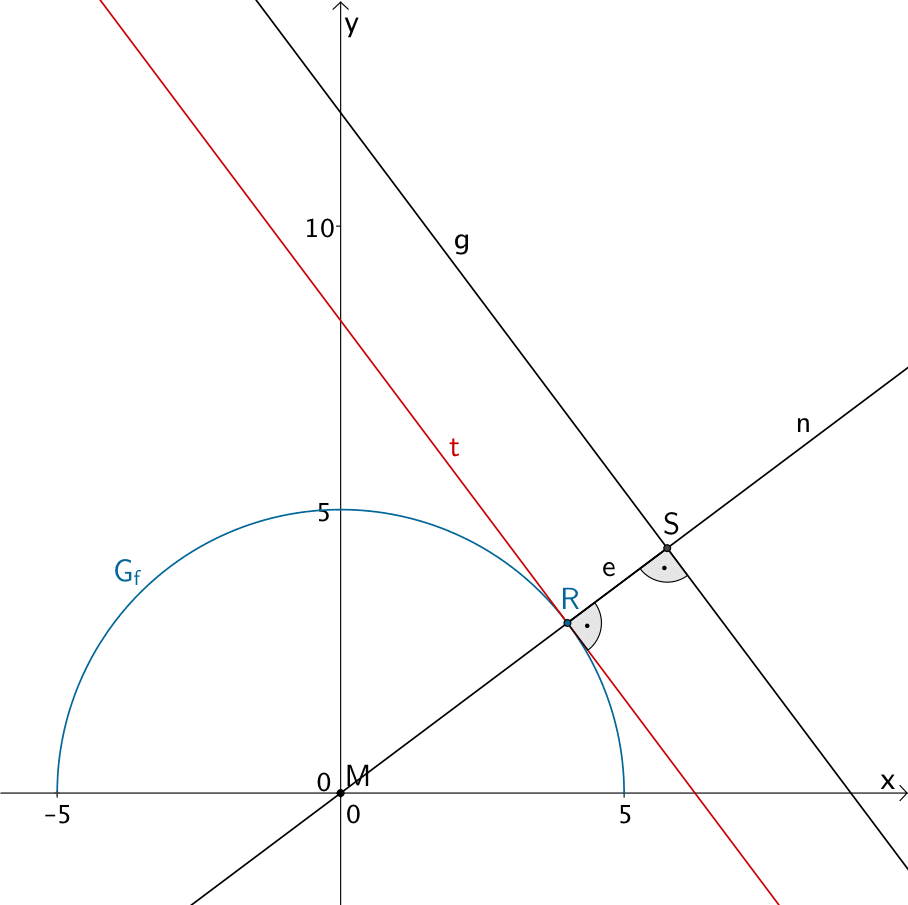
Der Punkt \(R\) ist derjenige Graphenpunkt von \(G_{f}\) (Tunnelwand), der zur Geraden \(g\) (Hangprofil) den kleinsten Abstand e hat. Die Normale \(n\) an \(G_{f}\) in Punkt \(R\) schneidet die Gerade \(g\) im Punkt \(S\) senkrecht, da \(t \parallel g\) gilt (vgl. Teilaufgabe 3d). Der kleinste Abstand \(e\) des Punktes \(R\) zur Geraden \(g\) ist gleich der Länge der Strecke \([RS]\).
1. Gleichung der Normale \(n\) in \(R\) aufstellen
Aus Teilaufgabe 3a ist bekannt, dass der Graph der Funktion \(f\) ein Halbkreis mit dem Mittelpunkt \(M(0|0)\) ist.
Jede Normale in einem beliebigen Punkt eines Kreises verläuft radial, d.h. durch den Mittelpunkt des Kreises. Folglich ist die Normale \(n\) in Punkt \(R\) eine Ursprungsgerade.
Die Steigung \(m_{n}\) der Normale \(n\) lässt sich entweder mithilfe der Steigung \(m_{t}\) der Tangente \(t\) aus Teilaufgabe 3b bestimmen oder anhand der Punkte \(R\) und \(M\).
\(M(0|0) \in n\), \(R(4|3) \in n\), \(m_{t} = -\frac{4}{3}\) (vgl. Teilaufgabe 3d)
Anwendung der Differetialrechnung:
Tangentensteigung und Normalensteigung
Tangentensteigung: \(m_{T} = f'(x_0)\)
Normalensteigung: \(m_{N} = -\dfrac{1}{f'(x_0)}\)
(vgl. Merkhilfe)
\[m_{n} = -\frac{1}{f'(4)} = -\frac{1}{m_{t}}\]
oder
Steigung \(m\) einer Gerade
\[m = \frac{\Delta y}{\Delta x} = \frac{y_B - y_A}{x_B - x_A}\]
\[m = \tan \alpha \quad (\alpha \neq 90^{\circ})\]
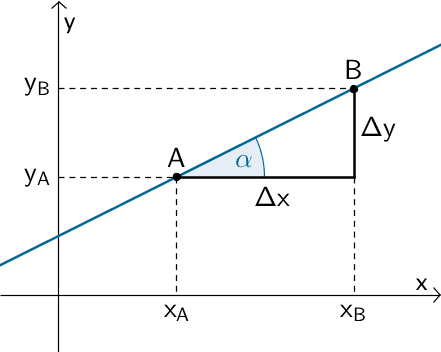
\[m_{n} = \frac{y_{R} - y_{M}}{x_{R} - x_{M}}\]
\[\Longrightarrow \quad n \colon y = m_{n} \cdot x\]
2. Schnittpunkt \(S\) der Normalen \(n\) und der Geraden \(g\) berechnen
Die Gleichung der Normale \(n\) und die Gleichung der Geraden \(g\) bilden ein lineares Gleichungssystem. Für die Berechnung der \(x\)-Koordinate des Schnittpunkts \(S\) der Normalen \(n\) und der Geraden \(g\) werden die Funktionsterme der Gleichungen von \(n\) und \(g\) gleichgesetzt, und die entstehende Gleichung nach \(x\) aufgelöst.
\[\begin{align*} n \colon y &= m_{n} \cdot x \\[0.8em] \wedge \enspace g \colon y &= -\frac{4}{3}x + 12 \end{align*}\]
\[\Longrightarrow \quad n \cap g \colon m_{n} \cdot x = -\frac{4}{3}x + 12\]
\(\Longrightarrow \quad x_{S}\) und \(y_{S} = g(x_{S}) = n(x_{S})\)
\[\Longrightarrow \quad S(x_{S}|y_{S})\]
3. Kleinsten Abstand \(e\) berechnen
Der kleinste Abstand \(e\) der Tunnelwand vom Hangprofil entspricht dem Abstand \(d(R;g)\) des Punktes \(R\) von der Geraden \(g\) in Metern.
Abstand \(\overline{PQ}\) zweier Punkte \(P(x_P|y_P)\) und \(Q(x_Q|y_Q)\) in der Ebene:
\[\overline{PQ} = \sqrt{(x_Q - x_P)^2 + (y_Q - y_P)^2}\]
\[\begin{align*}e &= d(R;g) \\[0.8em] &= d(R;S) \\[0.8em] &= \overline{RS} \\[0.8em] &= \sqrt{(x_{S} - x_{R})^{2} + (y_{S} - y_{R})^{2}} \end{align*}\]


