Geben Sie \(f(-2)\) an und zeichnen Sie \(G_f\) unter Berücksichtigung der bisherigen Ergebnisse in ein Koordinatensystem ein (Platzbedarf im Hinblick auf die folgenden Aufgaben: \(-3 \leq y \leq 7\)).
(3 BE)
Lösung zu Teilaufgabe 1d
Funktionswert f(-2)
\[\begin{align*} f(-2) &= 2 - \sqrt{12 - 2 \cdot (-2)} \\[0.8em] &= 2 - \sqrt{16} \\[0.8em] &= 2 - 4 \\[0.8em] &= -2 \end{align*}\]
Zeichnung von \(G_f\) unter Berücksichtigung der bisherigen Ergebnisse
Bisherige Ergebnisse:
\[N\,(4|0)\,, \quad S_{y}\,(0|2 - 2\sqrt{3})\]
\[f(-2) = -2\,; \quad f(6) = 2\]
\[D_f = \; ]-\infty;6]\,; \quad W_f = \; ]-\infty;2]\]
\(G_f\) ist für alle \(x \in D_f\) streng monoton steigend.
\[\lim \limits_{x\,\to\,-\infty} f(x) = -\infty\,; \quad \lim \limits_{x\,\to\,6} f'(x) = \infty\]
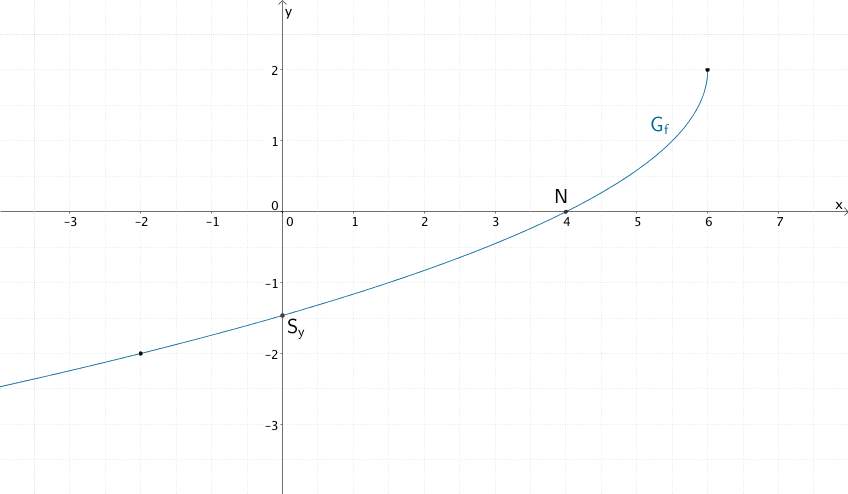
Graph der Funktion \(f\)


