Abbildung 1 zeigt ein Hinderniselement in einem Skate-Park.
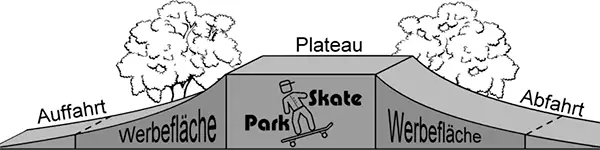Abb. 1
Die Auffahrt des symmetrischen Hinderniselements geht in ein horizontal verlaufendes Plateau über, an das sich die Abfahrt anschließt. Die vordere und die hintere Seitenfläche verlaufen senkrecht zum horizontalen Untergrund. Um die vordere Seitenfläche mathematisch beschreiben zu können, wird ein kartesisches Koordinatensystem so gewählt, dass die \(x\)-Achse die untere Begrenzung und die \(y\)-Achse die Symmetrieachse der betrachteten Fläche darstellt. Das Plateau erstreckt sich im Modell im Bereich \(-2 \leq x \leq 2\). Die Profillinie der Abfahrt wird für \(2 \leq x \leq 8\) durch den Graphen der in Aufgabe 1 untersuchten Funktion f beschrieben (vgl. Abbildung 2). Dabei entspricht eine Längeneinheit im Koordinatensystem einem Meter in der Realität.
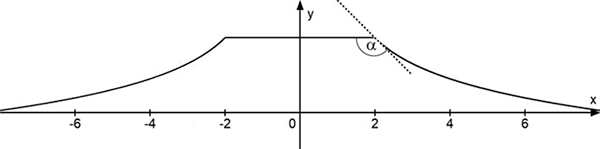Abb. 2
Erläutern Sie die Bedeutung des Funktionswerts \(f(2)\) im Sachzusammenhang und geben Sie den Term der Funktion \(q\) an, deren Graph \(G_{q}\) für \(-8 \leq x \leq -2\) die Profillinie der Auffahrt im Modell beschreibt.
(2 BE)
Lösung zu Teilaufgabe 2a
Profillinie der Abfahrt: \(f(x) = 2 - \ln{(x - 1)}; \; 2 \leq x \leq 8\)
Bedeutung des Funktionswerts \(f(2)\) im Sachzusammenhang
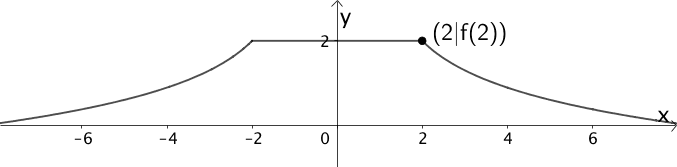
\(f(2)\) gibt die Höhe des Plateaus über dem horizontalen Untergrund in Metern an.
Term der Funktion \(q\), deren Graph \(G_{q}\) für \(-8 \leq x \leq -2\) die Profillinie der Auffahrt im Modell beschreibt
Die Profillinie der Auffahrt und die Profillinie der Abfahrt sind zur \(y\)-Achse symmetrisch (vgl. Angabe).
Spiegeln von Funktionsgraphen
Spiegelung an der \(x\)-Achse: \(g(x) = -f(x)\)
Spiegelung an der \(y\)-Achse: \(h(x) = f(-x)\)
\[\Longrightarrow \quad q(x) = f(-x) = 2 - \ln{(-x - 1)}\]
